Para evaluar con precisión la calidad de las estructuras de acero en servicio es necesario determinar el grado y la resistencia del acero. Ésta es la base para realizar pruebas y evaluaciones fiables.
El método convencional para determinar la resistencia del acero es extraer muestras de la estructura para realizar pruebas de tracción, pero este enfoque puede causar daños a la estructura original y puede no ser viable para ciertas estructuras.
Por lo tanto, es fundamental utilizar métodos de prueba no destructivos para calcular la calidad y la resistencia del acero.
Investigadores nacionales e internacionales han investigado métodos de prueba no destructivos para determinar la resistencia del acero en sitios de ingeniería. Se centraron principalmente en la composición química y la dureza y desarrollaron algunas fórmulas empíricas.
Lectura relacionada: Dureza del metal: la guía definitiva (con tabla de dureza)
Estas fórmulas empíricas se pueden clasificar en dos tipos:
El primer tipo implica calcular la resistencia a la tracción en función de la composición química, como se especifica en la fórmula de la norma técnica GB/T 50621-2010 para pruebas in situ de estructuras de acero. Sin embargo, la resistencia de los materiales de acero se ve afectada por la composición química y el proceso de fabricación. (como fundición, forjado, laminado y tratamiento térmico), por lo que depender únicamente de la composición química para calcular la resistencia del acero puede generar una desviación significativa.
El segundo tipo implica calcular la resistencia a la tracción en función de la dureza. Las investigaciones han demostrado que existe una correlación positiva entre la dureza y la resistencia a la tracción del acero. La resistencia a la tracción de los materiales se puede estimar a partir de los resultados de las pruebas de dureza, que es un método ampliamente utilizado en la práctica de la ingeniería.
Actualmente, las principales normas nacionales que se pueden utilizar para este fin son GB/T 33362-2016 Conversión de valores de dureza de materiales metálicos y GB/T 1172-1999 Conversión de dureza y resistencia de metales ferrosos. GB/T 33362-2016 es equivalente a la conversión ISO 18265:2013 de valores de dureza de materiales metálicos. La tabla de conversión de dureza para aceros no aleados, aceros de baja aleación y aceros fundidos de la Tabla A.1 de esta norma se obtuvo mediante pruebas de comparación con durómetros verificados y calibrados en diferentes laboratorios por la Asociación Alemana de Ingenieros Metalúrgicos. GB/T 1172-1999 se obtuvo mediante pruebas e investigaciones exhaustivas realizadas por instituciones como la Academia China de Metrología. La Tabla 2 de la norma proporciona principalmente el índice de conversión aplicable al acero con bajo contenido de carbono.
Sin embargo, ninguno de estos estándares proporciona datos confiables con significación estadística para la incertidumbre de los valores de conversión, y se desconoce el rango de desviación de los resultados de la conversión. Los investigadores estudiaron la correlación entre dureza y resistencia del acero utilizado en la construcción de estructuras de acero mediante análisis de regresión y la compararon con las normas nacionales, que sirven como verificación y complemento a las normas GB/T 33362-2016 y GB/T 1172-1999. . También discutieron el método de detección adecuado para sitios de proyectos de estructuras de acero mediante la incorporación de instrumentos de detección portátiles existentes.
1. Muestra de prueba
Los objetos de investigación de este estudio son las placas de acero Q235 y Q345 comúnmente utilizadas en ingeniería de estructuras metálicas.
Lectura relacionada : Acero Q235 vs Q345
Para garantizar muestras representativas, se recolectaron 162 placas de acero de 86 fabricantes de estructuras de acero en la provincia de Jiangsu, que comprenden 82 piezas de placas de acero Q235 y 80 piezas de placas de acero Q345. Las especificaciones de espesor de las placas de acero fueron 6, 8, 10, 12, 14, 18, 20 y 30 mm.
Las placas de acero se procesaron en muestras de tiras de 20 mm x 400 mm y se llevaron a cabo pruebas de tracción utilizando una máquina de prueba de tracción servo electrohidráulica controlada por microcomputadora de acuerdo con los requisitos de GB/T 228.1-2010.
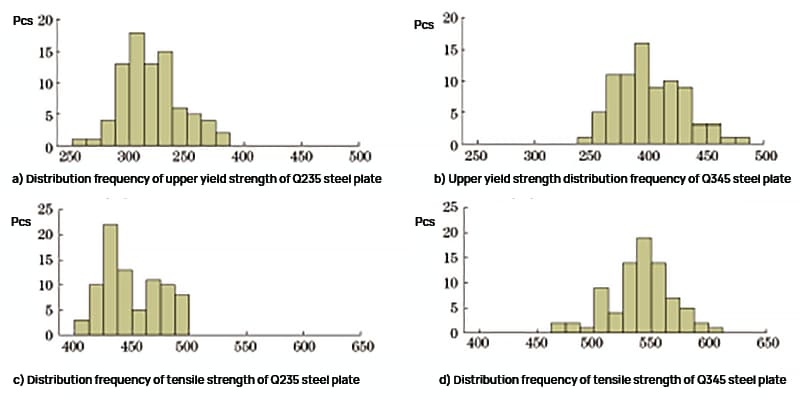
Los resultados de las pruebas de límite elástico y resistencia a la tracción superiores de las placas de acero Q235 y Q345 se analizaron estadísticamente y la frecuencia de distribución se muestra en la Figura 1.
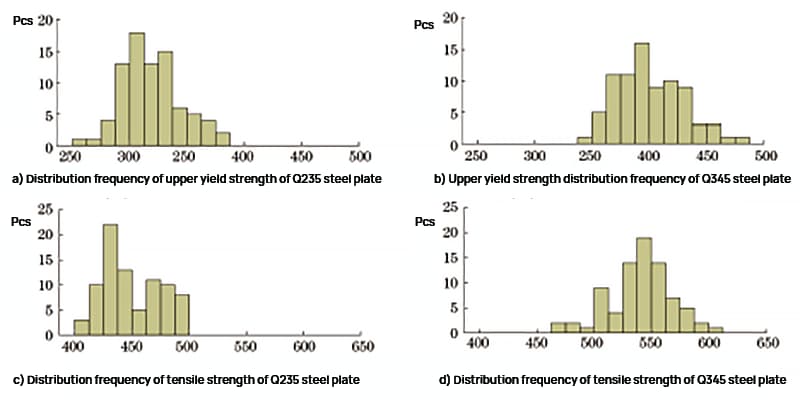
Fig. 1 Frecuencia de distribución de resistencia de la placa de acero Q235 y la placa de acero Q345
Como se muestra en la Figura 1, el rango de límite elástico superior de la placa de acero Q235 es de 261 a 382 MPa, y el rango de resistencia a la tracción es de 404 a 497 MPa. El rango de límite elástico superior de la placa de acero Q345 es de 345 a 477 MPa, y el rango de resistencia a la tracción es de 473 a 607 MPa.
La distribución de frecuencia de intensidad es aproximadamente normal y los resultados de las pruebas están en línea con los datos de la inspección diaria, lo que indica que las muestras son altamente representativas.
2. Resultados y análisis de las pruebas.
Las muestras de prueba se recolectaron y procesaron de acuerdo con los requisitos de la norma y se sometieron a pruebas de dureza Rockwell, dureza Vickers, dureza Brinell y tracción.
Para realizar el análisis de regresión de los resultados de los ensayos de dureza y resistencia se utilizó el método de mínimos cuadrados y se utilizó el software SPSS.
2.1 Correlación entre dureza y resistencia Rockwell
2.1.1 Resultados y análisis de la prueba de dureza Rockwell
La superficie de la muestra se lijó con una amoladora para garantizar que quedara plana y lisa. Se seleccionó la escala B y el instrumento se calibró utilizando un bloque de dureza estándar. La prueba de dureza Rockwell se llevó a cabo de acuerdo con los requisitos de la prueba de dureza Rockwell de materiales metálicos GB/T 230.1-2018, parte 1: método de prueba. Se midieron tres puntos para cada muestra y se obtuvo el valor promedio.
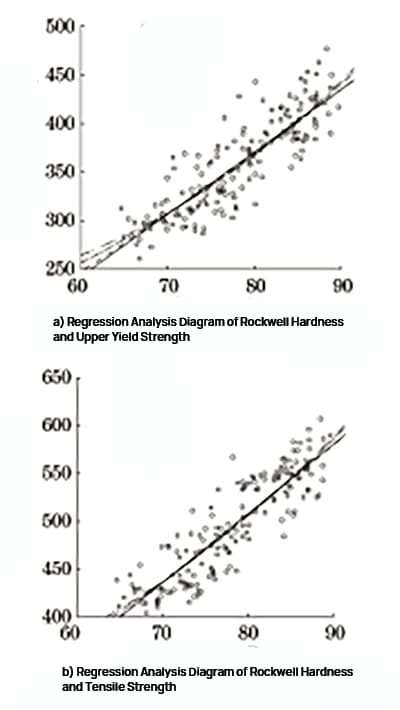
Fig. 2 Análisis de regresión de la dureza y resistencia de Rockwell.
Se utilizó el software SPSS para realizar análisis de regresión lineal, regresión cuadrática, regresión de potencia y regresión exponencial sobre la dureza Rockwell, el límite elástico superior y la resistencia a la tracción. El diagrama del análisis de regresión se representa en la Figura 2 y los resultados del análisis de regresión se presentan en la Tabla 1 y la Tabla 2.
Tabla 1 Datos del modelo de regresión de dureza de Rockwell y límite elástico superior
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | constante | b1 | b2 | |
| Exponente cuadrático lineal | 0,736 | 446.897 | 0.000 | -143.077 | 6.426 | 0.081 |
| 0,741 | 227,290 | 0.000 | 341.852 | -6,141 | ||
| 0.740 | 456.461 | 0.000 | 0,828 | 1.392 | ||
| 0.744 | 464,965 | 0.000 | 86.806 | 0,018 | ||
Tabla 2 Datos del modelo de regresión de dureza Rockwell y resistencia a la tracción
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | constante | b1 | b2 | |
| Exponente cuadrático lineal | 0.780 | 565.900 | 0.000 | -71,394 | 7.241 | 0,074 |
| 0.783 | 286,412 | 0.000 | 372,980 | -4.274 | ||
| 0,778 | 560.887 | 0.000 | 3.477 | 1,137 | ||
| 0,782 | 574,207 | 0.000 | 155.315 | 0,015 | ||
Como se indica en las Tablas 1 y 2, la dureza Rockwell tiene una fuerte correlación con la resistencia, y la correlación con la resistencia a la tracción es más fuerte en comparación con el límite elástico máximo.
De los cuatro modelos de regresión entre dureza y resistencia Rockwell, todos tienen una significancia P inferior a 0,05 y una bondad de ajuste cercana a R 2 .
Dado que la relación de conversión entre la dureza Rockwell y la resistencia a la tracción del acero con bajo contenido de carbono especificada en la norma es similar al modelo polinómico, se recomienda utilizar el modelo cuadrático para la conversión.
La fórmula después del ajuste es:
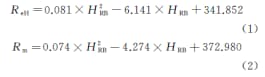
Donde: R Eh es el límite superior de rendimiento; R i es la resistencia a la tracción; HRB es la dureza Rockwell.
2.1.2 Análisis de desviación relativa de los resultados de conversión
Con base en el modelo de regresión cuadrática ajustado, se calcularon y analizaron estadísticamente las desviaciones relativas entre los valores convertidos del límite elástico superior y la resistencia a la tracción y los resultados de las pruebas de tracción. El tamaño de la muestra fue 162 y los resultados se presentan en la Tabla 3.
Las desviaciones relativas siguen una distribución normal y la distribución de frecuencia se muestra en la Figura 3.
Tabla 3 Tabla estadística de desviación relativa de la dureza Rockwell a la resistencia
| Elementos estadísticos | Valor mínimo | Máximo | Desviación promedio | Referencia estándar |
| Desviación relativa del valor de conversión del límite elástico superior | -16.56 | +16.61 | ±5,46 | 6.84 |
| Desviación relativa de la resistencia a la tracción convertida | -13:31 | +11.16 | ±4,12 | 5.03 |
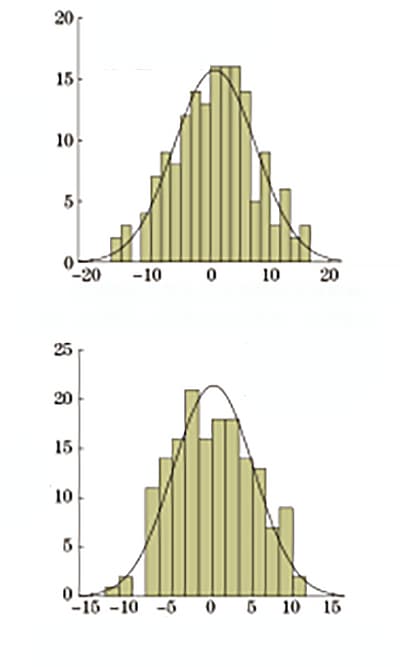
Fig. 3 Desviación relativa de la dureza Rockwell en relación con la resistencia
2.1.3 Comparación con el valor de conversión estándar nacional
La Figura 4 muestra una comparación del valor de conversión de resistencia a la tracción especificado en la norma, el valor de conversión de la fórmula de regresión cuadrática ajustada y el diagrama de dispersión de la relación correspondiente entre la dureza Rockwell y la resistencia a la tracción, todo en el mismo gráfico.
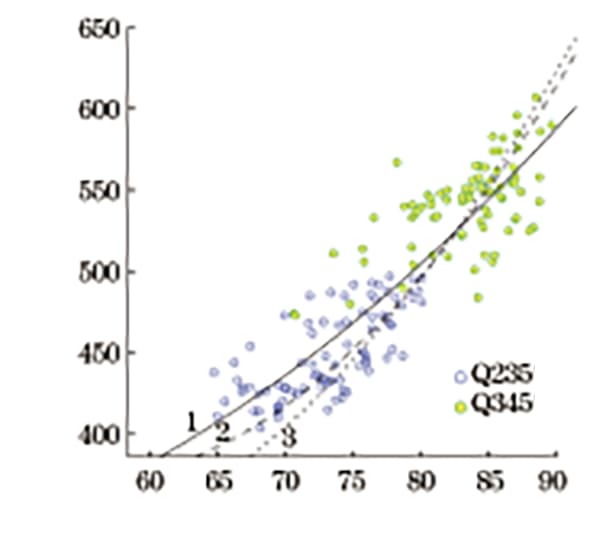
Fig. 4 Cuadro comparativo de resistencia a la tracción convertida por dureza Rockwell
Como se ve en la Figura 4, la tendencia general de las tres curvas es consistente. El valor de conversión de resistencia a la tracción dado en GB/T 1172-1999 es similar al del autor, con una desviación promedio del 2,7% y una desviación máxima del 5,7% en el rango de 370 a 630 MPa.
Sin embargo, el valor de conversión de resistencia a la tracción proporcionado en GB/T 33362-2016 es menor para el acero Q235 (con una resistencia a la tracción en el rango de 370 a 500 MPa) y mayor para el acero Q345 (con una resistencia a la tracción en el rango de 470 a 500 MPa). 630MPa).
2.2 Correlación entre dureza y resistencia Vickers
2.2.1 Proceso de prueba de dureza Vickers y análisis de resultados.
La superficie de la muestra se pulió con un molinillo y el instrumento se calibró con un bloque de dureza estándar. La prueba de dureza Vickers se llevó a cabo de acuerdo con los requisitos de la prueba de dureza Vickers de materiales metálicos GB/T 4340.1-2009, parte 1: método de prueba. Se midieron tres puntos para cada muestra y se obtuvo el valor promedio.
Se utilizó el software SPSS para realizar análisis de regresión lineal, regresión cuadrática, regresión de potencia y regresión exponencial sobre la dureza Vickers, el límite elástico superior y la resistencia a la tracción. El diagrama del análisis de regresión se representa en la Figura 5 y los resultados del análisis de regresión se presentan en la Tabla 4 y la Tabla 5.
Tabla 4 Datos del modelo de regresión de dureza Vickers y límite elástico superior
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | constante | b1 | b2 | |
| Exponente cuadrático lineal | 0,727 | 426,980 | 0.000 | -9,332 | 2.530 | 0.002 |
| 0,728 | 212,272 | 0.000 | 27.358 | 2020 | ||
| 0.731 | 433.768 | 0.000 | 2,215 | 1.021 | ||
| 0.731 | 435.083 | 0.000 | 126.740 | 0.007 | ||
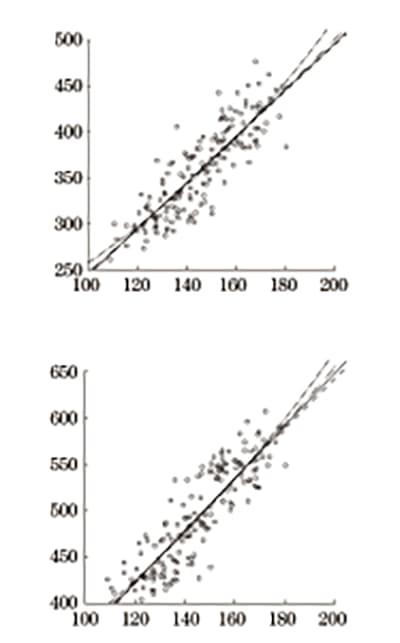
Fig. 5 Análisis de regresión de dureza y resistencia Vickers.
Tabla 5 Datos del modelo de regresión de dureza y resistencia a la tracción Vickers
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | Constante | b1 | b2 | |
| Exponente cuadrático lineal | 0,753 | 486,507 | 0.000 | 84.099 | 2.818 | 0.002 |
| 0,753 | 241,944 | 0.000 | 133,182 | 2,136 | ||
| 0,748 | 475,262 | 0.000 | 8.189 | 0.823 | ||
| 0,751 | 483,330 | 0.000 | 213,597 | 0.006 | ||
Como se indica en las Tablas 4 y 5, la dureza Vickers tiene una fuerte correlación con la resistencia, y la correlación con la resistencia a la tracción es más fuerte en comparación con el límite elástico máximo.
De los cuatro modelos de regresión entre dureza y resistencia Vickers, todos tienen una significación P inferior a 0,05 y una bondad de ajuste cercana a R 2 .
Dado que la relación de conversión entre la dureza Vickers y la resistencia a la tracción del acero con bajo contenido de carbono especificada en la norma es cercana a una relación lineal, se recomienda utilizar la relación lineal para la conversión.
La fórmula después del ajuste es:
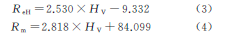
Donde: H V es la dureza Vickers.
2.2.2 Análisis de desviación relativa de los resultados de conversión
Con base en el modelo de regresión lineal ajustado, se calcularon y analizaron estadísticamente las desviaciones relativas entre los valores convertidos del límite elástico superior y la resistencia a la tracción y los resultados de las pruebas de tracción. El tamaño de la muestra fue 162 y los resultados se presentan en la Tabla 6.
Las desviaciones relativas siguen una distribución normal y la distribución de frecuencia se muestra en la Figura 6.
Tabla 6 Tabla estadística de desviación relativa de la dureza Vickers para la resistencia
| Elementos estadísticos | Valor mínimo | Máximo | Desviación promedio | Referencia estándar |
| Desviación relativa del valor de conversión del límite elástico superior | -7:30 pm. | +17.55 | ±5,75 | 7.09 |
| Desviación relativa de la resistencia a la tracción convertida | -12:32 | +15.83 | ±4,88 | 5.44 |
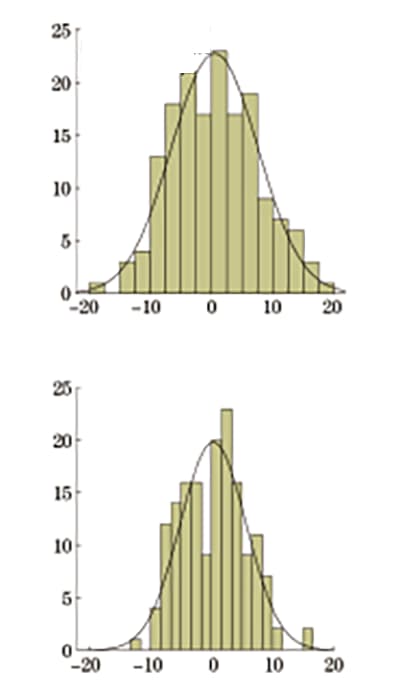
Fig. 6 Desviación relativa de la dureza Vickers convertida en resistencia.
2.2.3 Comparación con el valor de conversión estándar nacional
La Figura 7 muestra una comparación del valor de conversión de la resistencia a la tracción especificado en la norma, el valor de conversión de la fórmula de regresión lineal obtenida por el autor y el diagrama de dispersión de la relación correspondiente entre la dureza Vickers y la resistencia a la tracción, todo en el mismo gráfico.
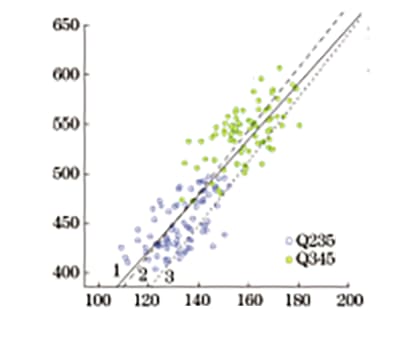
Fig. 7 Cuadro comparativo de resistencia a la tracción convertida por dureza Vickers
Como se ve en la Figura 7, la tendencia general de las tres curvas es consistente. El valor de conversión de resistencia a la tracción especificado en GB/T 1172-1999 es muy cercano al valor de conversión obtenido por el autor. En el rango de 370 a 630 MPa, la diferencia entre ellos aumenta ligeramente al aumentar el valor de dureza, con una desviación promedio del 1,2% y una desviación máxima del 3,3%. Sin embargo, el valor de conversión de resistencia a la tracción proporcionado en GB/T 33362-2016 es generalmente menor.
2.3 Correlación entre dureza y resistencia Brinell
2.3.1 Proceso de prueba de dureza Brinell y análisis de resultados
La superficie de la muestra se pulió con un molinillo para asegurar una rugosidad superficial de no más de 1,6 µm. El instrumento se calibró con un bloque de dureza estándar y la prueba de dureza Brinell se realizó de acuerdo con los requisitos de GB/T 231.1-2018 Prueba de dureza Brinell de materiales metálicos Parte 1: Método de prueba. Se utilizó un penetrador de carburo con un diámetro de 10 mm y la fuerza de prueba fue de 29,42 kN. Se midieron tres puntos para cada muestra y se obtuvo el valor promedio.
Se utilizó el software SPSS para realizar análisis de regresión lineal, regresión cuadrática, regresión de potencia y regresión exponencial en dureza Brinell, límite elástico superior y resistencia a la tracción. El diagrama del análisis de regresión se representa en la Figura 8 y los resultados del análisis de regresión se presentan en la Tabla 7 y la Tabla 8.
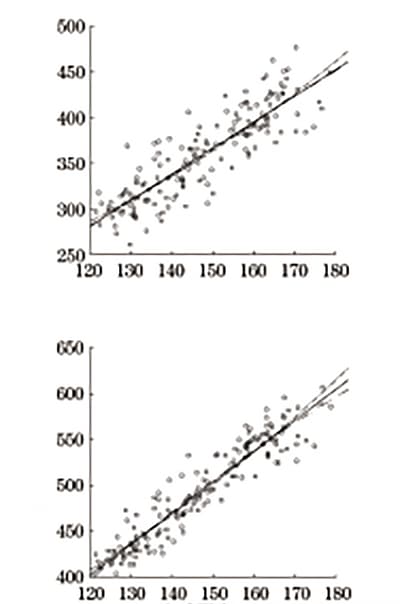
Fig. 8 Análisis de regresión de dureza y resistencia Brinell
Tabla 7 Datos del modelo de regresión de dureza Brinell y límite elástico superior
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | constante | b1 | b2 | |
| Exponente cuadrático lineal | 0,756 | 495,403 | 0.000 | -59,965 | 2.846 | -0.001 |
| 0,758 | 246,186 | 0.000 | -86,188 | 3,205 | ||
| 0,757 | 497,365 | 0.000 | 1.048 | 1,168 | ||
| 0,756 | 494,881 | 0.000 | 110,318 | 0.008 | ||
Tabla 8 Datos del modelo de regresión de dureza Brinell y resistencia a la tracción
| Ecuación | Resumen Modelo | Parámetro del modelo | ||||
| R 2 | F | P Significado | constante | b1 | b2 | |
| Exponente cuadrático lineal | 0,887 | 1253.313 | 0.000 | -2.613 | 3.377 | -0.001 |
| 0,888 | 631.852 | 0.000 | -225,666 | 6.424 | ||
| 0,889 | 1286.205 | 0.000 | 3,204 | 1.009 | ||
| 0,886 | 1238,834 | 0.000 | 179.073 | 0.007 | ||
Como se indica en las Tablas 7 y 8, la dureza Brinell tiene una fuerte correlación con la resistencia, y la correlación con la resistencia a la tracción es más fuerte en comparación con el límite elástico máximo.
De los cuatro modelos de regresión entre dureza y resistencia Brinell, todos tienen una significancia P inferior a 0,05 y una bondad de ajuste cercana a R 2 .
Dado que la relación de conversión entre la dureza Brinell del acero al carbono y la resistencia a la tracción especificada en la norma es cercana a una relación lineal, se recomienda utilizar una relación lineal para la conversión.
La fórmula ajustada es:
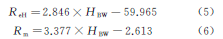
Donde: H PN es la dureza Brinell.
2.3.2 Análisis de desviación relativa de los resultados de conversión
De acuerdo con el modelo de regresión lineal ajustado, las desviaciones relativas entre los valores convertidos del límite elástico superior y la resistencia a la tracción y los resultados de las pruebas de tracción se calculan respectivamente, y las desviaciones relativas se analizan estadísticamente.
Las estadísticas son 162 y los resultados se muestran en la Tabla 9.
Las desviaciones relativas son básicamente una distribución normal y la distribución de frecuencia se muestra en la Fig.
Tabla 9 Tabla estadística de desviación relativa de la dureza Brinell a la resistencia
| Elementos estadísticos | Valor mínimo | Máximo | Desviación promedio | Referencia estándar |
| Desviación relativa del valor de conversión del límite elástico superior | -16,78 | +18.67 | ±5,38 | 6.75 |
| Desviación relativa de la resistencia a la tracción convertida | -9.25 | +8.55 | ±2,89 | 3.59 |
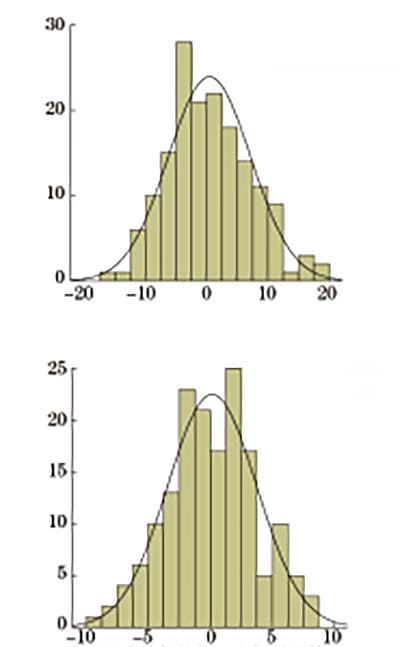
Fig. 9 Desviación relativa de la dureza Brinell convertida en resistencia.
2.3.3 Comparación con el valor de conversión estándar nacional
En GB/T 1172-1999, la relación entre la fuerza de prueba y el diámetro de la bola del penetrador de la prueba de dureza Brinell es 10.
Las pruebas de autor se llevan a cabo de acuerdo con GB/T 231.1-2018. Con referencia a lo dispuesto en la norma, la relación entre la fuerza de prueba y el diámetro de la bola penetradora es 30.
Por lo tanto, ya no se compara con GB/T 1172-1999 en comparación con el valor de conversión estándar nacional.
El valor de conversión estándar de resistencia a la tracción proporcionado en GB/T 33362-2016, el valor de conversión de la fórmula de regresión lineal ajustada por el autor y el diagrama de dispersión de la relación correspondiente entre la dureza Brinell y la resistencia a la tracción se comparan en el mismo gráfico, como se muestra en Figura 10.
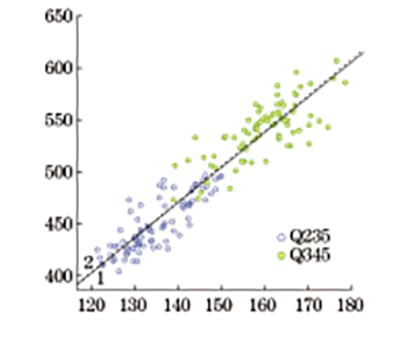
Fig. 10 Cuadro comparativo de resistencia a la tracción convertida por dureza Brinell
Se puede ver en la Figura 10 que el valor de conversión de resistencia a la tracción proporcionado en GB/T 33362-2016 casi coincide con la curva de regresión de resistencia a la tracción ajustada por el autor, con una desviación promedio del 0,4% y una desviación máxima del 1,2% dentro de 370 -630MPa.
En los últimos años, el rápido desarrollo de varios durómetros portátiles ha aportado una gran comodidad a las pruebas in situ.
En la actualidad, se pueden comprar en el mercado muchos tipos de durómetros Rockwell portátiles y durómetros Brinell portátiles.
El equipo es portátil, fácil de operar, rápido de medir y la precisión de la detección también cumple con los requisitos de las normas nacionales, lo que es adecuado para la detección de ingeniería in situ.
También hay varios equipos de procesamiento portátiles para el tratamiento de superficies de muestras, que pueden cumplir con los requisitos de prueba.
Por lo tanto, es factible utilizar la dureza Rockwell y la dureza Brinell para calcular la resistencia del acero en la inspección de campo de estructuras de acero.
3. Conversión de dureza en resistencia para metales ferrosos (GB/T 1172-1999)
| Tenacidad | Resistencia a la tracción σb /MPa |
||||||||||||||||
| rockwell | Superficie de Rockwell | Vickers | Brinell | Acero carbono | Acero cromado | Acero al cromo y bario | Acero al cromo níquel | Acero al cromo molibdeno | Acero al cromo, níquel y molibdeno | Acero al cromo-manganeso-silicio | Acero de ultra alta resistencia | Acero inoxidable | No se especifica ningún tipo específico de acero. | ||||
| CDH | HORA | HR15N | HR30N | HR45N | Alta tensión | HB30D 2 |
d 10. 2 d 5. 4 d 2.5 /mm |
||||||||||
| 17 | – | 67,3 | 37,9 | 15.6 | 211 | 211 | 4.15 | 73,6 | 706 | 705 | 772 | 726 | – | 757 | – | 703 | 724 |
| 18 | – | 67,8 | 38,9 | 16.8 | 216 | 216 | 4.11 | 753 | 723 | 719 | 779 | 737 | – | 769 | – | 719 | 737 |
| 19 | – | 68.3 | 39,8 | 18 | 221 | 220 | 4.07 | 771 | 739 | 735 | 788 | 749 | – | 782 | – | 737 | 752 |
| 20 | – | 68,8 | 40,7 | 19.2 | 226 | 225 | 4.03 | 790 | 757 | 751 | 797 | 761 | – | 796 | – | 754 | 767 |
| 21 | – | 69.3 | 41,7 | 20.4 | 231 | 227 | 4 | 809 | 775 | 767 | 807 | 775 | – | 810 | – | 773 | 782 |
| 22 | – | 69,8 | 42,6 | 21,5 | 237 | 234 | 3.95 | 829 | 794 | 785 | 819 | 789 | – | 825 | – | 792 | 799 |
| 23 | – | 70.3 | 43,6 | 22.7 | 243 | 240 | 3.91 | 849 | 814 | 803 | 831 | 805 | – | 840 | – | 812 | 816 |
| 24 | – | 70,8 | 44,5 | 23.9 | 249 | 245 | 3.87 | 870 | 834 | 823 | 845 | 821 | – | 856 | – | 832 | 835 |
| 25 | – | 71,4 | 45,5 | 25.1 | 255 | 251 | 3.83 | 892 | 855 | 843 | 860 | 838 | – | 874 | – | 853 | 854 |
| 26 | – | 71,9 | 46,4 | 26.3 | 261 | 257 | 3.78 | 914 | 876 | 864 | 876 | 857 | 876 | 892 | – | 875 | 874 |
| 27 | – | 72,4 | 47.3 | 27,5 | 268 | 263 | 3.74 | 937 | 898 | 886 | 893 | 877 | 897 | 910 | – | 897 | 895 |
| 28 | – | 73 | 48.3 | 28,7 | 274 | 269 | 3.7 | 961 | 920 | 909 | 912 | 897 | 918 | 930 | – | 919 | 917 |
| 29 | – | 73,5 | 49.2 | 29,9 | 281 | 276 | 3.65 | 984 | 943 | 933 | 932 | 919 | 941 | 951 | – | 942 | 940 |
| 30 | – | 74.1 | 50.2 | 31.1 | 289 | 283 | 3.61 | 1009 | 967 | 959 | 953 | 943 | 966 | 973 | – | 966 | 904 |
| 31 | – | 74,7 | 51.1 | 32.3 | 296 | 291 | 3.56 | 1034 | 991 | 985 | 976 | 967 | 991 | 996 | – | 990 | 989 |
| 32 | – | 75.2 | 52 | 33,5 | 304 | 298 | 3.52 | 1060 | 1016 | 1013 | 1001 | 993 | 1018 | 1020 | – | 1015 | 1015 |
| 33 | – | 75,8 | 53 | 34,7 | 312 | 306 | 3.48 | 1086 | 1042 | 1042 | 1027 | 1020 | 1047 | 1046 | – | 1041 | 1042 |
| 34 | – | 76,4 | 53,9 | 25,9 | 320 | 314 | 3.43 | 1113 | 1068 | 1072 | 1054 | 1049 | 1077 | 1073 | – | 1067 | 1070 |
| 35 | – | 77 | 54,8 | 37 | 329 | 323 | 3.39 | 1141 | 1095 | 1104 | 1084 | 1079 | 1108 | 1101 | – | 1095 | 1100 |
| 36 | – | 77,5 | 55,8 | 38.2 | 338 | 332 | 3.34 | 1170 | 1124 | 1136 | 1115 | 1111 | 1141 | 1130 | – | 1126 | 1131 |
| 37 | – | 78.1 | 56,7 | 39,4 | 347 | 341 | 3.3 | 1200 | 1153 | 1171 | 1148 | 1144 | 1176 | 1161 | – | 1153 | 1163 |
| 38 | – | 78,7 | 57,6 | 40,6 | 357 | 350 | 3.26 | 1231 | 1184 | 1206 | 1132 | 1179 | 1212 | 1194 | – | 1184 | 1197 |
| 39 | 70 | 79,3 | 58,6 | 41,8 | 367 | 360 | 3.21 | 1263 | 1216 | 1243 | 1219 | 1216 | 1250 | 1228 | 1218 | 1216 | 1232 |
| 40 | 70,5 | 79,9 | 59,5 | 43 | 377 | 370 | 3.17 | 1296 | 1249 | 1282 | 1257 | 1254 | 1290 | 1264 | 1267 | 1250 | 1268 |
| 41 | 71.1 | 80,5 | 60,4 | 44.2 | 388 | 380 | 3.13 | 1331 | 1284 | 1322 | 1298 | 1294 | 1331 | 1302 | 1315 | 1286 | 1307 |
| 42 | 71,6 | 81.1 | 61.3 | 45,4 | 399 | 391 | 3.09 | 1367 | 1322 | 1364 | 1340 | 1336 | 1375 | 1342 | 1362 | 1325 | 1347 |
| 43 | 72.1 | 81,7 | 62.3 | 46,5 | 411 | 401 | 3.05 | 1405 | 1361 | 1407 | 1385 | 1379 | 1420 | 1384 | 1409 | 1366 | 1389 |
| 44 | 72,6 | 82.3 | 63.2 | 47,7 | 423 | 413 | 3.01 | 1445 | 1403 | 1452 | 1431 | 1425 | 1467 | 1427 | 1455 | 1410 | 1434 |
| 45 | 73.2 | 82,9 | 64.1 | 48,9 | 436 | 424 | 2,97 | 1488 | 1448 | 1498 | 1480 | 1472 | 1516 | 1474 | 1502 | 1457 | 1480 |
| 46 | 73,7 | 83,5 | sesenta y cinco | 50.1 | 449 | 436 | 2.93 | 1533 | 1497 | 1547 | 1531 | 1522 | 1567 | 1522 | 1550 | 1508 | 1529 |
| 47 | 74.2 | 84 | 65,9 | 51.2 | 462 | 449 | 2,89 | 1581 | 1549 | 1597 | 1584 | 1573 | 1620 | 1573 | 1600 | 1563 | 1581 |
| 48 | 74,7 | 84,6 | 66,8 | 52,4 | 478 | 401 | 2,85 | 1631 | 1605 | 1649 | 1640 | 1626 | 1676 | 1627 | 1652 | 1623 | 1635 |
| 49 | 75,3 | 85.2 | 67,7 | 53,6 | 493 | 474 | 2.81 | 1686 | 1666 | 1702 | 1698 | 1682 | 1733 | 1683 | 1707 | 1688 | 1692 |
| 50 | 75,8 | 85,7 | 68,6 | 54,7 | 509 | 488 | 2.77 | 1744 | 1731 | 1758 | 1758 | 1739 | 1793 | 1742 | 1765 | 1759 | 1753 |
| 51 | 76,3 | 86,3 | 69,5 | 55,9 | 525 | 501 | 2.73 | – | 1803 | 1816 | 1821 | 1799 | 1854 | 1804 | 1827 | – | 1817 |
| 52 | 76,9 | 86,8 | 70,4 | 57.1 | 543 | – | – | – | 1881 | 1875 | 1887 | 1861 | 1918 | 1870 | 1894 | – | 1885 |
| 53 | 77,4 | 87,4 | 71.3 | 58.2 | 561 | – | – | – | – | 1937 | 1955 | 1925 | 1985 | 1938 | 1967 | – | 1957 |
| 54 | 77,9 | 87,9 | 72.2 | 59,4 | 579 | – | – | – | – | 2000 | 2025 | – | – | 2010 | 2045 | – | 2034 |
| 55 | 78,5 | 88,4 | 73.1 | 60,5 | 599 | – | – | – | – | 2066 | 2098 | – | – | 2086 | 2131 | – | 2115 |
| 56 | 79 | 88,9 | 73,9 | 61,7 | 620 | – | – | – | – | – | – | – | – | – | 2224 | – | 2201 |
| 57 | 79,5 | 89,4 | 74,8 | 62,8 | 642 | – | – | – | – | – | – | – | – | – | 2324 | – | 2293 |
| 58 | 80.1 | 89,8 | 75,6 | 63,9 | 664 | – | – | – | – | – | – | – | – | – | 2437 | – | 2391 |
| 59 | 80,6 | 90.2 | 76,5 | 65.1 | 688 | – | – | – | – | – | – | – | – | – | 2558 | – | 2496 |
| 60 | 81.2 | 90,6 | 77,3 | 66.2 | 713 | – | – | – | – | – | – | – | – | – | 2691 | – | 2607 |
| 61 | 81,7 | 91 | 78.1 | 67,3 | 739 | – | – | – | – | – | – | – | – | – | – | – | – |
| 62 | 82.2 | 91,4 | 79 | 68,4 | 766 | – | – | – | – | – | – | – | – | – | – | – | – |
| 63 | 82,8 | 91,7 | 79,8 | 69,5 | 795 | – | – | – | – | – | – | – | – | – | – | – | – |
| 64 | 83.3 | 91,9 | 80,6 | 70,6 | 825 | – | – | – | – | – | – | – | – | – | – | – | – |
| sesenta y cinco | 83,9 | 92.2 | 81.3 | 71,7 | 856 | – | – | – | – | – | – | – | – | – | – | – | – |
| 66 | 84,4 | – | – | – | 889 | – | – | – | – | – | – | – | – | – | – | – | – |
| 67 | 85 | – | – | – | 923 | – | – | – | – | – | – | – | – | – | – | – | – |
| 68 | 85,5 | – | – | – | 959 | – | – | – | – | – | – | – | – | – | – | – | – |
| 69 | 86.1 | – | – | – | 997 | – | – | – | – | – | – | – | – | – | – | – | – |
| 70 | 86,6 | – | – | – | 1037 | – | – | – | – | – | – | – | – | – | – | – | – |
3. Conclusión
(1) La dureza Rockwell, la dureza Vickers y la dureza Brinell tienen una buena correlación con la resistencia. Con base en la prueba del material, se obtiene la fórmula de conversión de dureza Rockwell, dureza Vickers y dureza y resistencia Brinell, y la desviación de conversión relativa está dentro del rango permitido de diseño.
La desviación relativa entre la dureza Brinell y la resistencia a la tracción es obviamente menor que la de la dureza Rockwell y la dureza Vickers.
(2) La resistencia a la tracción convertida a partir de la dureza Rockwell proporcionada en GB/T 33362-2016 es baja para el acero Q235 y alta para el acero Q345.
La resistencia a la tracción convertida a partir de la dureza Vickers es ligeramente menor.
La resistencia a la tracción convertida a partir de la dureza Brinell es consistente con los resultados de la prueba.
Los valores de resistencia a la tracción convertidos por dureza Rockwell y dureza Vickers dados en GB/T 1172-1999 están cerca de los resultados de la prueba.
(3) Combinado con los instrumentos portátiles de prueba de dureza y los equipos de procesamiento de muestras existentes, el uso de la dureza Rockwell y la dureza Brinell para calcular la resistencia del acero es operable en proyectos prácticos y puede aplicarse a la práctica de la ingeniería.