6 Factors Affecting Sheet Metal Bending Radius

Ideal bend radius

There must be a bending radius for sheet metal bending, it must not be too large or too small, and it must be chosen appropriately.

If the bending radius is too small, it will cause cracking at the bending position;

If the bending radius is too large, it is easy to recover.

However, you can use the V-channel machine to groove first and then bend. This way you will get a smaller bending radius.

The ideal bending radius of different thicknesses of various materials (internal bending radius) refer to the table below:

Metal	Annealing condition		Cold hardening state
	The corresponding position of the bending direction and fiber direction
	Vertical	Parallel	Vertical	Parallel
08, 10	0.1t	0.4t	0.4t	0.8t
15, 20	0.1t	0.5t	0.5t	1.0t
25, 30	0.2t	0.6t	0.6t	1.2t
45, 50	0.5t	1.0t	1.0t	1.7t
65 minutes	1.0t	2.0t	2.0t	3.0t
Aluminum	0.1t	0.35t	0.5t	1.0t
Brass	0.1t	0.35t	1.0t	2.0t
Soft brass	0.1t	0.35t	0.35t	0.8t
Semi-rigid brass	0.1t	0.35t	0.5t	1.2t
Phosphor bronze	/	/	1.0t	3.0t

The data in the table above is the preferred data for reference only. In fact, the rounded corners of the press brake are generally 0.3, and a small number of rounded corners of the press brake punch are 0.5.

For common low-carbon steel plates, anti-rust aluminum plates, yellow copper, purple copper, etc., the inner radius 0.2 is no problem, but for some high-carbon steels, hard aluminum, super-hard aluminum, the use of Radius 0.2 will lead to flexural fracture or outer radius cracking.

Factors that can affect the bend radius

What are the factors that can affect the bending radius of sheet metal?

There are several factors that can impact the bending radius of sheet metal, including the thickness of the metal, the material it is made of, the radius of the top punch, the bottom die, the applied bending force, and the working temperature.

I hope this article, based on my personal experience, is useful to readers.

Bending angle

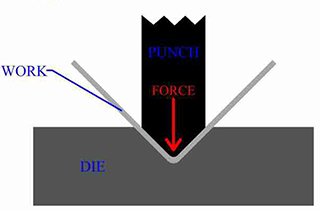
The bending angle of the sheet metal is the key factor that affects the bending tolerance.

For example, if you bend the sheet metal with a large radius, more bending allowance will be deducted; if it bends at an acute angle, less bending allowance will be deducted.

Sheet metal thickness

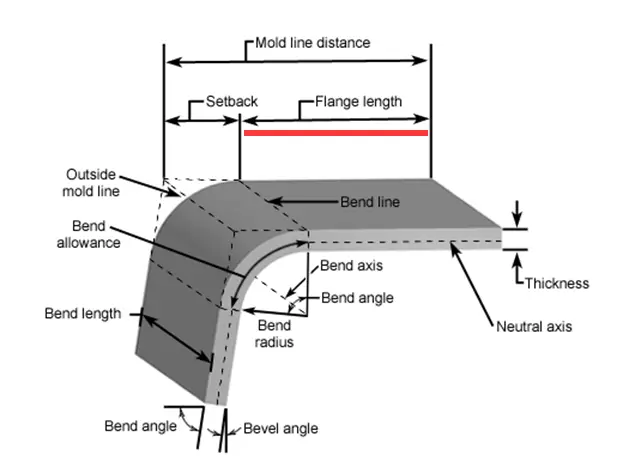
In practical applications, it has been observed that the radius of curvature increases as the thickness of the material increases.

We are aware that a thicker plate requires more bending force and a larger V-opening in the bottom die.

What then affects the curvature angle r?

Sheet Metal Material​​

Bending tolerance for sheets of the same thickness may vary slightly, demonstrating that material properties play a role in determining the bend radius.

The flexural strength of the material can directly influence the bending radius.

Although the material has an impact on the bending radius, it has limited effect in our actual use.

We can create a custom bending tolerance table for different materials.

Punch tip radius

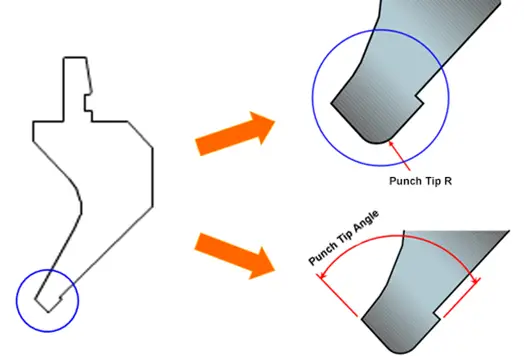
The standard radius of the bending die should not exceed r1, and the minimum punch radius should not be less than 1.

If there are no specific requirements for the bending radius, this will have a limited impact on the bending process.

However, for sheet metal bending that requires a specific bend radius less than 1 or significantly greater than 1, it is not determined by the top punch radius alone.

Therefore, the upper punch radius directly affects the final bend radius.

It is important to keep in mind that where the radius of the punch tip is greater than the radius generated by the V-die used in bending, this will affect the internal radius of the profile.

For example:

• 1mm mild steel to be bent
• Chosen die V = 8 mm, which, as shown below, produces an internal bending radius of 1 mm.

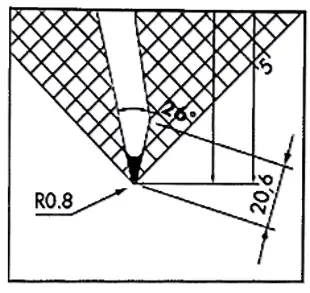
The internal radius of curvature will be:

• r= 1 mm, where the radius of the punch tip is smaller than Imm
• or r = punch tip radius where the punch tip radius is greater than 1 mm.

A typical example of this principle are represented by radius tool holders which can be used to obtain large radius bends in small dies. In this case, the required internal radius is produced by the shape of the punch tip.

Where instead you want to maintain the internal bending radius produced by the
die, the ideal rdius of the punch tip can be calculated with the following equation:

Ideal radius of the punch tip = (R produced by the die) x (2/3)

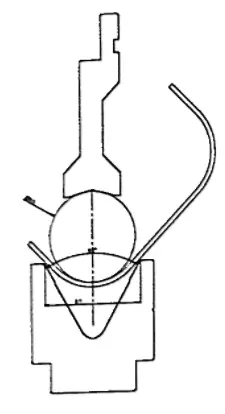
Using this relationship, the surface of the punch is proportional to the force required to bend the sheet metal, preventing the tip of the punch from penetrating the sheet metal. This avoids aesthetic problems or cracks in the material on the inside of the fold.

Furthermore, with a tip radius that is too small and with acute angles, it is possible for the sheet metal to be almost cut and for the profile to close over the punch, thus producing an angle different from that intended.

It is not always easy to fulfill the above-mentioned equation due to the lack of different bending radii at the ends in many workshops.

However, press brake operators should use the tip radius closest to the ideal. Especially for thick sheets, which require high force to be bent, operators must use appropriate punch tip radii to avoid sheet deformations, dimensional problems, or issues involving appearance or cracking.

Doubling Strength

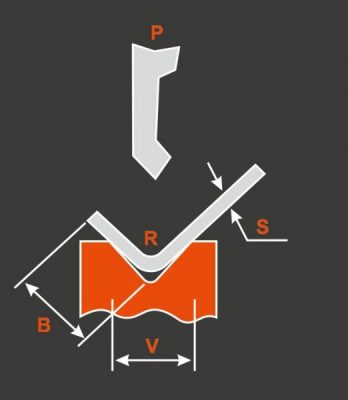
The thicker the sheet, the greater the resistance to bending deformation.

Therefore, the bending force must be adjusted accordingly.

The bending force cannot be increased constantly and must be adjusted to an appropriate level.

The bending force is directly proportional to the thickness of the metal sheet and inversely proportional to the width of the lower die groove.

When bending, the thickness of the sheet metal is fixed, and the width of the bottom die groove is selected based on the thickness of the metal.

As a result, the bending force becomes constant, determined by other factors.

The bending radius cannot be accurately determined without considering the bending force.

Bottom D that is

The width of the bottom die slot has a direct correlation with the sheet metal thickness.

In real-world applications, the radius of curvature increases as the thickness of the metal increases.

For the same sheet metal thickness, the bending radius may also vary depending on the width of the V-opening.

Therefore, it is clear that the width of the bottom groove of the die plays a crucial role in determining the radius of curvature.

Operating T temperature

Generally, the temperature of the working environment is the ambient temperature, which can be ignored.