The over-reinforced section is considered critical compared to the under-reinforced state. If reinforced too much, the section may fail suddenly and without warning due to the concrete breaking.
However, under conditions of insufficient gain, the section provides a stronger warning of failure.
Therefore, the designer must have a good knowledge of these conditions, namely equilibrium, under reinforced conditions and under reinforced conditions.
The article Balance, Over-Amplification and Under-Amplification For more information about each type and type of error you can refer to.
It should be noted that overly reinforced sections do not fail suddenly. They fail when the applied moment exceeds the moment capacity. If the section fails, there will be no warnings before failure, such as insufficiently reinforced sections.
Section assessment is carried out in accordance with BS standards (BS 8110).
This worked example verifies the following:
- Is the section overamplified?
- Bending moment capacity of the overreinforced section?
Let's check this with an example.
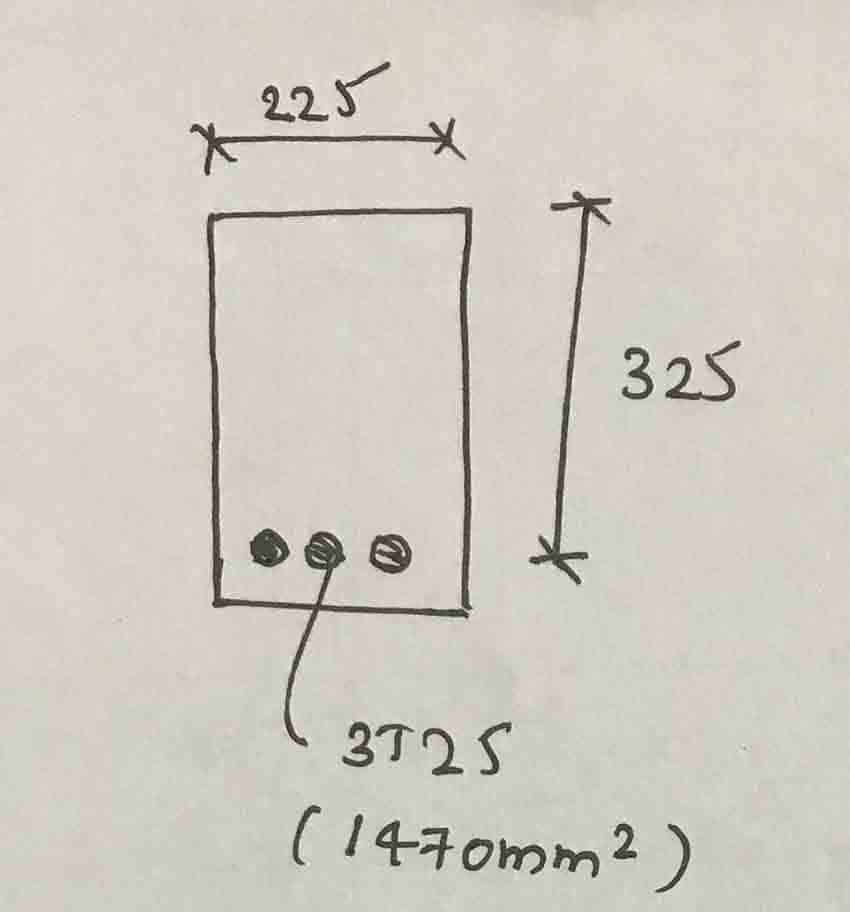
Look at the following section.
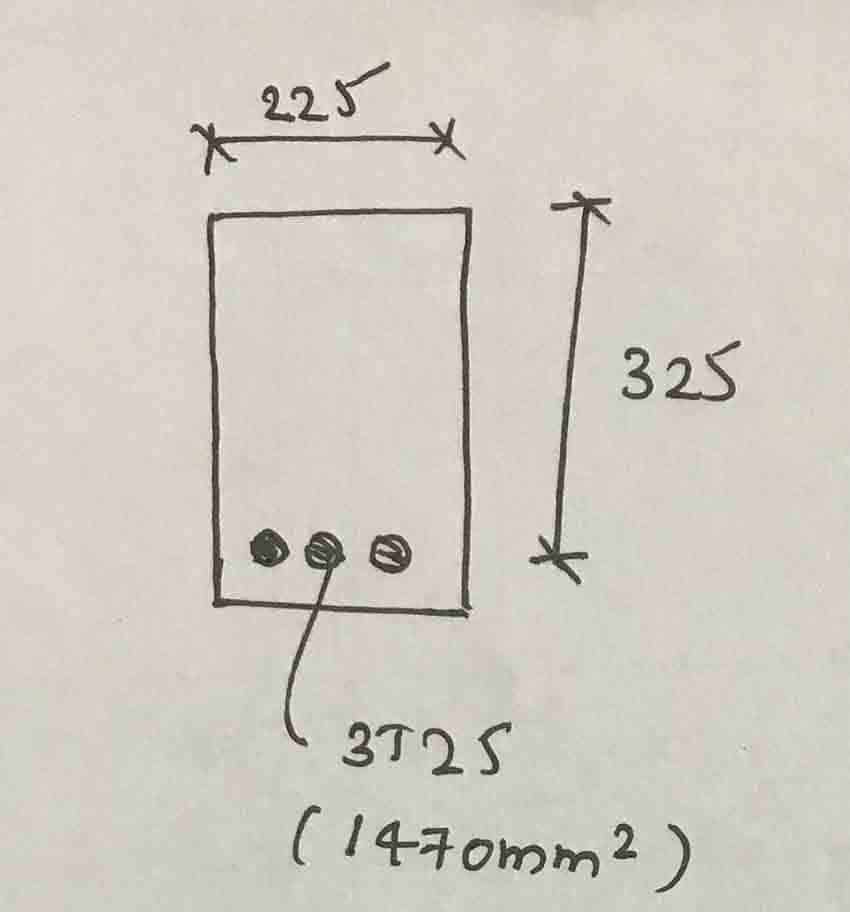

- Reinforced single section
- F cu = 25 N/mm 2
- fy = 460 N/mm 2
In this calculation we take into account the basic stress-strain relationship of the concrete cross section.
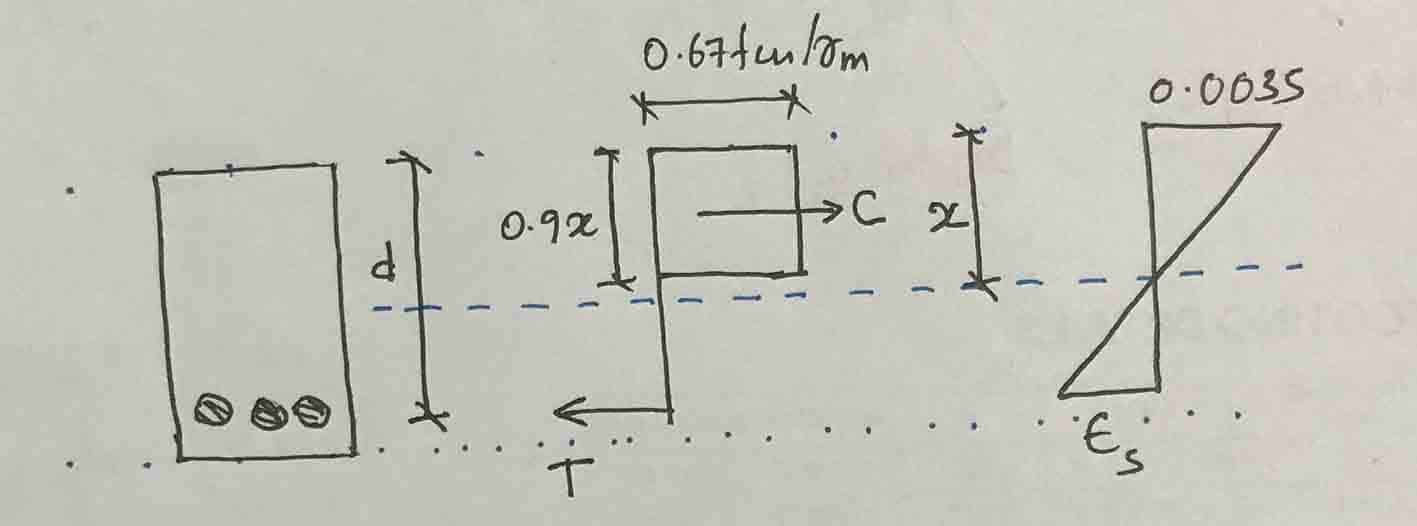
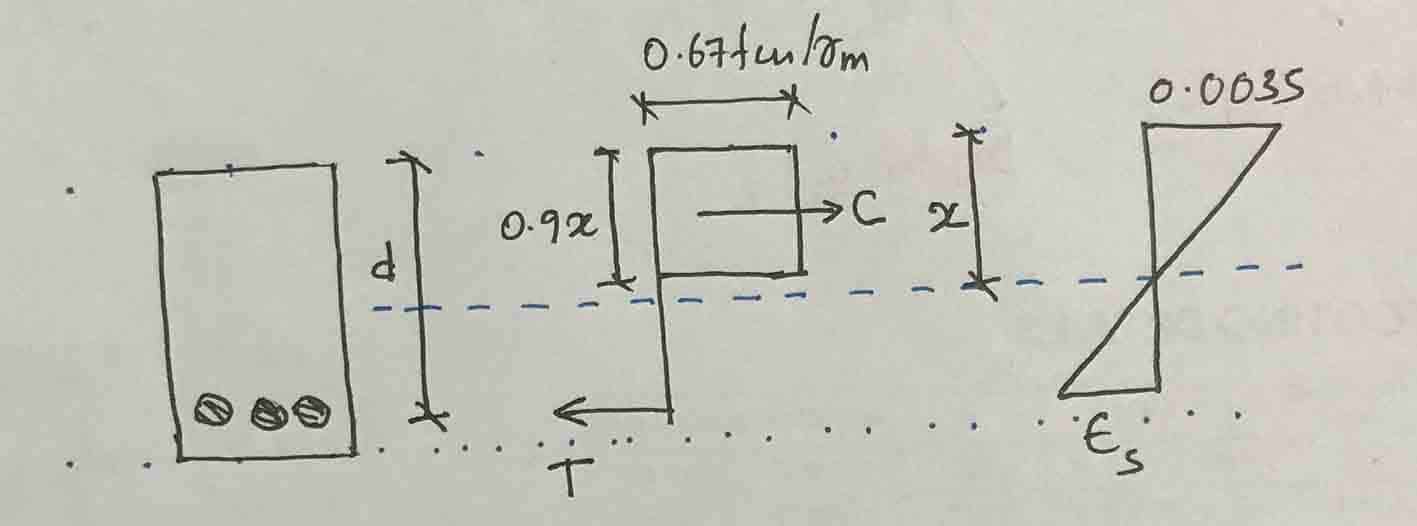
Let's first assume Reinforcement is return.
T = 0.87f j A S = 0.87 x 460 x 1470 = 588,294 N
C = (0.67f cu /ϒ M )(0.9x)b = (0.67×25/1.5)(0.9x)x225 = 226.125
C = T
226,125X = 588,294
x = 260mm
x/d = 260/325 = 0.8 > 0.64
The section is excessively reinforced.
The assumption that steel is durable is incorrect. We have to discover the real “x” by trial and error. This must be done until C = T.
Suppose x = 225 mm
C = 226125 X = 226125 x 225 = 508781.25N
Now calculate the strain of the steel to find the stress of the steel. The figure above can be used to calculate the deformation of steel.
εS = 0.0035(325-225)/225 = 0.0016
Now let's take a look at the stress-strain diagram.
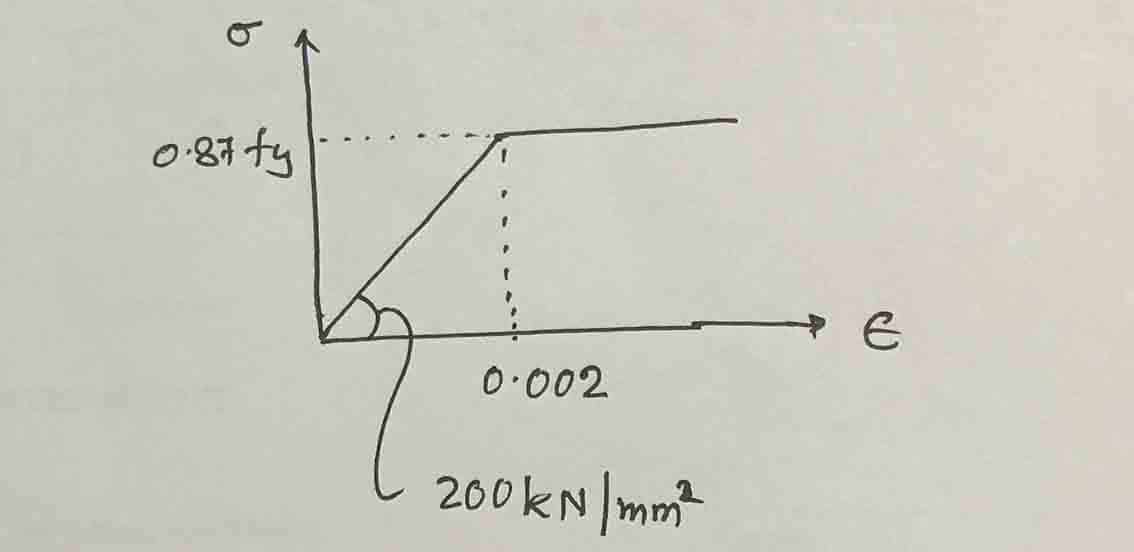
Steel tension, f S
F S = ε S E S = 0.0016 x 200×10 3 = 320 N/mm 2
T = 320 x 1470 = 470400N
C ≠ T
We need to perform several experiments until C = T assuming different depths of the neutral axis ( X ).
There is another method to directly determine the depth of the neutral axis. As the steel is not below the yield point (fs < 400 N/mm), 2 = 0.87 × 460).
Calculate the elongation of the steel, ε S
ε S / 0.0035 = (d – x) / x
ε S = 0.0035 (325 –x)/x
Now calculate the tension of the steel
F S = ε S E S = (0.0035 (325 – x)/x) 200×10 3
T=f S A S = (0.0035 (325 – x)/x) 200×10 3 x 1470
C = (0.67f cu /ϒ M )(0.9x)b = (0.67×25/1.5)(0.9x)x225 = 2278.125
T = C
(0.0035 (325 – x)/x) 200×10 3 x 1470 = 2278.125
X 2 + 451.69x – 146798.35 = 0
x = 218.91 or -679.6; x must be positive
Therefore x = 218.91 mm
Now calculate the bending capacity of the section
C = 2278.125 x 218.91 = 498704.34
Lever arm
Z = d – 0.45x = 325 – 0.45 x 218.91 = 226.49 mm
M = Cz = 498704.34 x 226.49/10 -6 = 112.95 kN m
The bending moment capacity of the over-reinforced section is 112.95 kNm.
You can find information about this in the Wikipedia article “Reinforced concrete”.