In the previous tutorial, the basic combinational arithmetic circuits like half adder, full adder, half subtractor and full subtractor were discussed in detail. Now, in this tutorial, the truth table and the derivation of Boolean expressions for all these circuits will be considered. With the derived Boolean expressions, all these circuits will be practically designed using digital ICs.
As discussed in the previous tutorial, the half adder can be constructed using an EX-OR gate and the AND gate. The full adder can be constructed using one OR gate, two EX-OR gates, and two AND gates. The half subtractor can be constructed using an EX-OR gate, a NOT gate and an AND gate. The complete subtractor can be constructed with one OR gate, two EX-OR gates, two AND gates, and two NOT gates. Therefore, to test all circuits, two AND gates, two EX-OR gates, two NOT gates and one OR gate are required. For the AND gate, IC 7408 can be used, which has four integrated AND gates. For the OR gate, 7432 IC can be used, which has four built-in OR gates. For EX-OR gate, IC 7486 can be used, which has four built-in EX-OR gates. For NOT gate, IC 7404 can be used which has six built-in NOT gates. The input to the digital circuits built from these ICs can be provided by a 2V DC source while the supply voltage to the ICs can be provided by a 5V DC source. The 5V DC source can be built using a battery and 7805 IC. The same voltage can be reduced to inputs using a variable resistor. The output can be checked by connecting LEDs to the respective digital output pins.
So, let's start testing the basic combinational circuits with digital ICs mentioned above. 
Circuit diagrams –
The Half adder has the following circuit diagram –
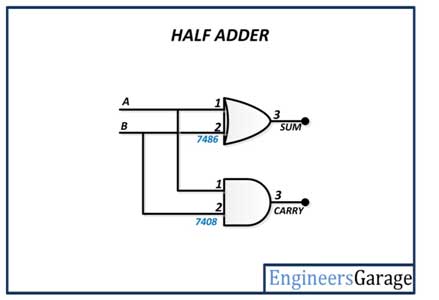
Fig. 1: Half adder circuit diagram
The Full Adder has the following circuit diagram –
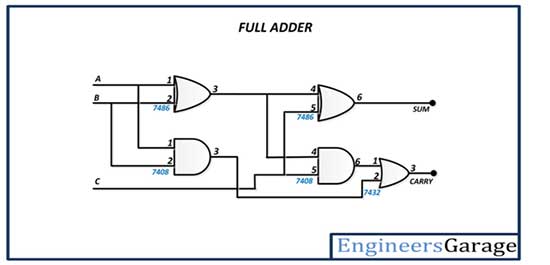
Fig. 2: Full Adder Circuit Diagram
The half subtractor has the following circuit diagram –
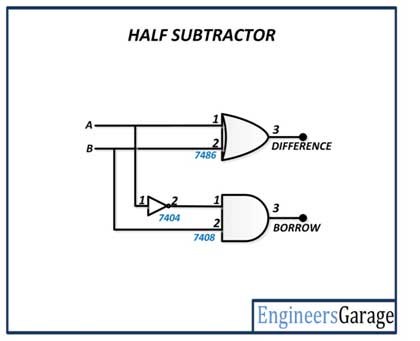
Fig. 3: Subtractor Half Circuit Diagram
The complete subtractor has the following circuit diagram –
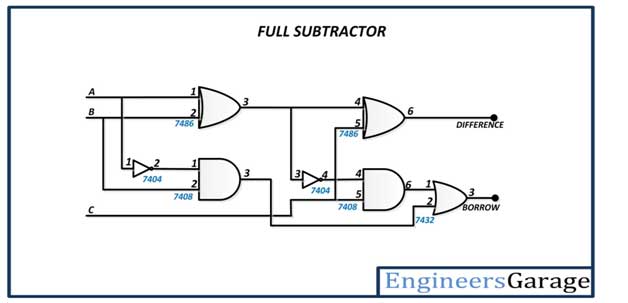
Fig. 4: Complete Subtractor Circuit Diagram
Circuit Connections –
All combinational arithmetic circuits are built by interconnecting logic gates. Each combinational circuit has its own truth table, where each output is linked to the inputs by some Boolean function. The circuits are built by interconnecting the logic gate ICs. The following logic gate ICs are used in constructing the circuits –
7408 IC – The 7408 IC has 2-input quadruple AND gates. The IC has the following pin configuration –
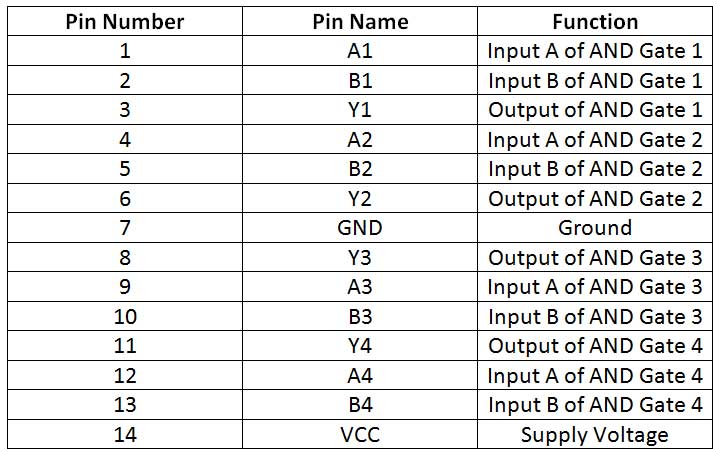
Fig. 5: Table listing the pin configuration of the 7408 IC
The IC has the following pin diagram –
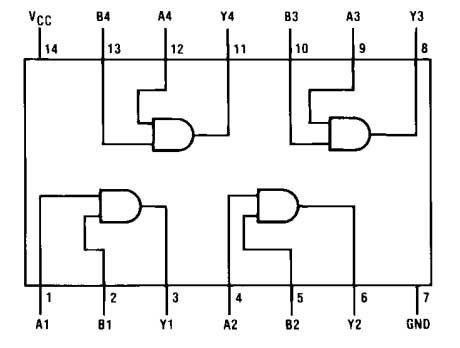
Fig. 6: Pin Diagram of 7408 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the AND gate inputs must be 2V for logic high and 0V for logic low. The output of the AND gates has a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on a positive logic system. The propagation delay during transit from LOW to HIGH at the output is 27 ns, while the propagation delay during transit from HIGH to LOW at the output is 19 ns.
7432 IC – The 7432 IC has 2-input quadruple OR gates. The IC has the following pin configuration –
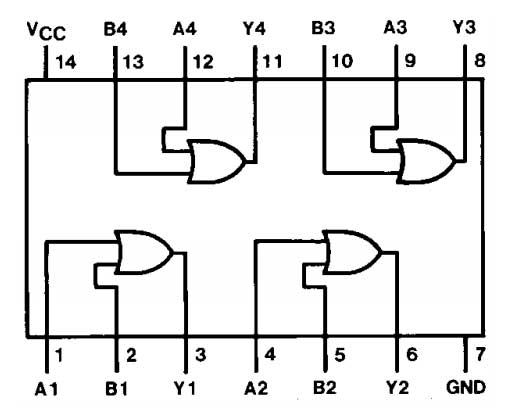
Fig. 7: Table listing the pin configuration of the 7432 IC
The IC has the following pin diagram –
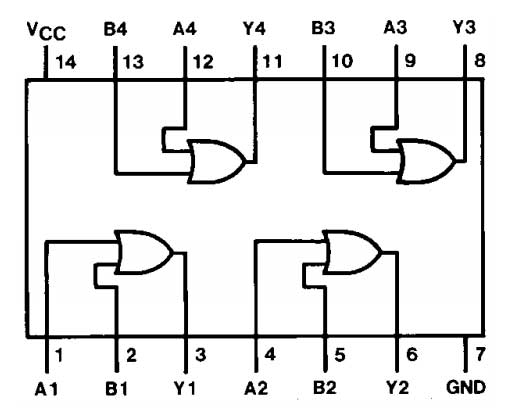
Fig. 7: Pin diagram of 7432 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the OR gates must be 2V for logic high and 0V for logic low. The output of the OR gates has a voltage of 3.4 V for logic high and 0.35 V for logic low. The IC operates on a positive logic system. The propagation delay during transit from LOW to HIGH at the output is 3 to 15 ns, while the propagation delay during transit from HIGH to LOW at the output is also 3 to 15 ns.
7486 IC – The 7486 IC has 2-input quad EX-OR gates. The IC has the following pin configuration –
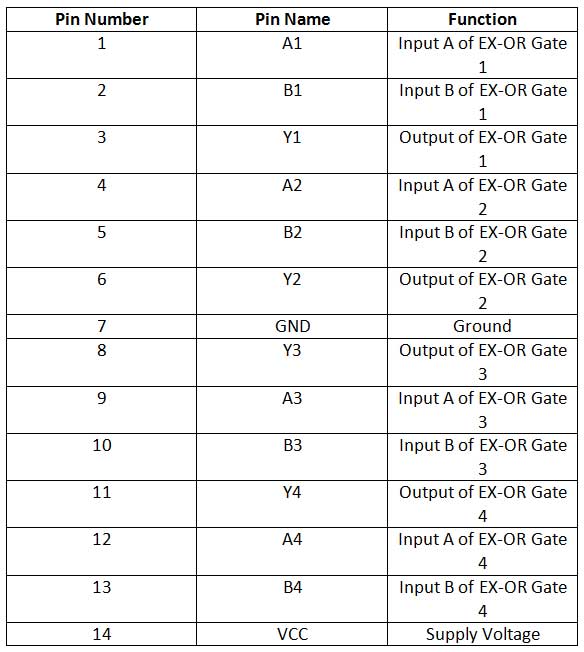
Fig. 8: Table listing the pin configuration of the 7486 IC
The IC has the following pin diagram –
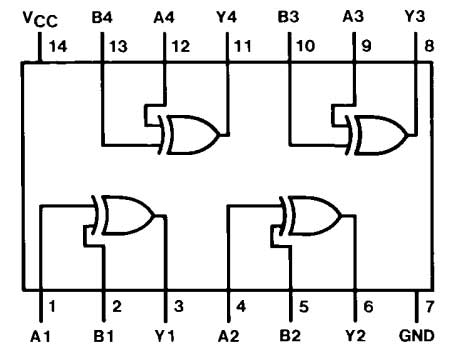
Fig. 9: Pin Diagram of 7486 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the EX-OR gates must be 2V for logic high and 0V for logic low. The output of the EX-OR gates has a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on a positive logic system. The propagation delay during the transition from LOW to HI at the output is 23 ns if other inputs are low and 30 ns if other inputs are high, while the propagation delay during the transition from HI to LOW at the output is 17 ns if other inputs are low and 22 ns if other inputs are high.
7404 IC – The 7404 IC has six inverter ports. The IC has the following pin configuration –
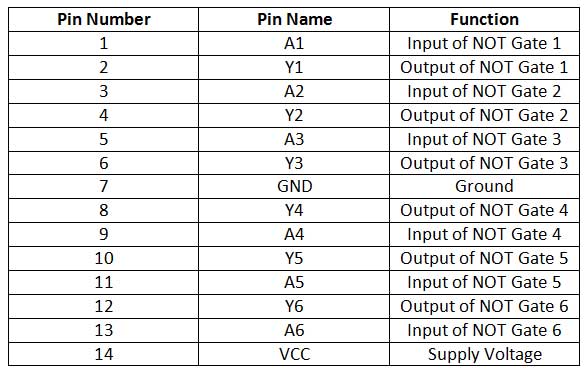
Fig. 10: Table listing the pin configuration of the 7404 IC
The IC has the following pin diagram –
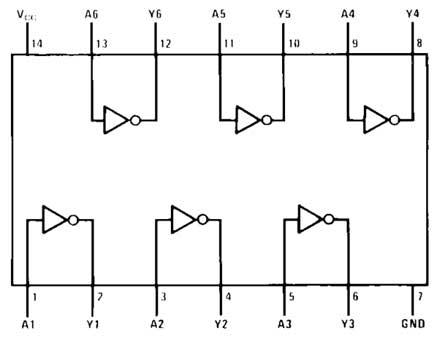
Fig. 11: Pin Diagram of 7404 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the NOT gates must be 2 V for logic high and 0.8 V for logic low. The output of the NOT gates has a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on a positive logic system. The propagation delay during transit from LOW to HIGH at the output is 22 ns, while the propagation delay during transit from HIGH to LOW at the output is 15 ns.
It should be noted that the selected ICs have compatible input, output and power voltage levels. They are taken from a common family (74XX series) of digital ICs.
The half adder is constructed by connecting the inputs to an EX-OR gate (pins 1 and 2 of the 7486 IC) and an AND gate (pins 1 and 2 of the 7408 IC). The Sum bit is taken from the output of the EX-OR gate (pin 3 of the 7486 IC) and the carry is taken from the output of the AND gate (pin 3 of the 7408 IC).
The full adder is constructed by connecting the inputs to an EX-OR gate (pins 1 and 2 of the 7486 IC) and an AND gate (pins 1 and 2 of the 7408 IC). The output of the first EX-OR gate (pin 3 of the 7486 IC) is connected to the input of the second EX-OR gate (pin 4 of the 7486 IC) and the input of the second AND gate (pin 4 of the 7408 IC). The Carry input is connected to another input of the second EX-OR gate (pin 5 of the 7486 IC) and another input of the second AND gate (pin 5 of the 7408 IC). The sum bit is taken from the output of the second EX-OR gate (pin 6 of the 7486 IC). The output of the second AND gate (pin 6 of the 7408 IC) is connected to an input of the OR gate (pin 1 of the 7432 IC) and the output of the first AND gate (pin 3 of the 7408 IC) is connected to another input of the OR gate (pin 2 of 7432 IC). The execution is taken from the output of the OR gate (pin 3 of the 7432 IC).
The half subtractor is constructed by connecting the inputs to an EX-OR gate (pins 1 and 2 of the 7486 IC) and connecting one input to the NOT gate input (pin 1 of the 7404 IC) and one directly to the input of an AND gate (pin 2 of the 7408 IC). The output of the NOT gate (pin 2 of the 7404 IC) is connected to the input of the AND gate (pin 1 of the 7408 IC). The difference bit is taken from the output of the EX-OR gate (pin 3 of the 7486 IC) and the borrow bit is taken from the output of the AND gate (pin 3 of the 7408 IC).
The complete subtractor is constructed by connecting the inputs to the first EX-OR gate (pins 1 and 2 of the 7486 IC) and connecting one input to the input of the first NOT gate (pin 1 of the 7404 IC) and one directly to the input of the first AND gate. port (pin 2 of the 7408 IC). The output of the first NOT gate (pin 2 of the 7404 IC) is connected to the input of the first AND gate (pin 1 of the 7408 IC). The output of the first EX-OR gate (pin 3 of the 7486 IC) is connected to the input of the second EX-OR gate (pin 4 of the 7486 IC) and the input of the second NOT gate (pin 3 of the 7404 IC). The Carry input is connected to another input of the second EX-OR gate (pin 5 of the 7486 IC) and another input of the second AND gate (pin 5 of the 7408 IC). The difference bit is taken from the output of the second EX-OR gate (pin 6 of the 7486 IC). The output of the second AND gate (pin 6 of the 7408 IC) is connected to an input of the OR gate (pin 1 of the 7432 IC) and the output of the first AND gate (pin 3 of the 7408 IC) is connected to another input of the OR gate (pin 2 of 7432 IC). The loan is taken from the output of the OR gate (pin 3 of the 7432 IC).
How the circuit works –
Each combinational circuit has its own truth table and respective Boolean expressions for the outputs. The circuits constructed above and their expected outputs are discussed below –
Half Adder
The binary adder is the basic arithmetic circuit, as the operation of adding binary numbers is a fundamental task in computing. Binary addition follows the following rules –
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10
In the first three operations, each binary addition gives the sum as one bit i.e. 0 or 1. But the fourth addition operation gives a sum consisting of two binary digits. In this case, the least significant bit is called the sum bit, while the most significant bit is called the carry bit.
The half adder has the following truth table –
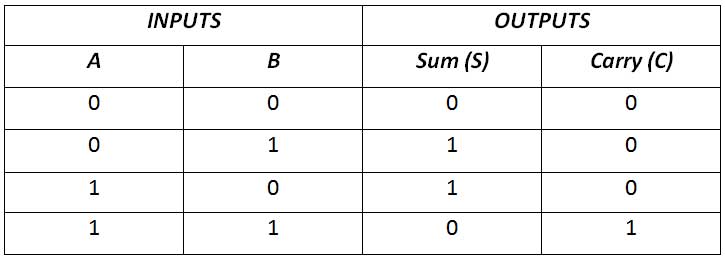
Fig. 12: Half Adder Truth Table
From the above truth table, the following K maps are drawn to derive the Boolean expressions for the sum and carry output –
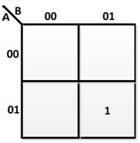
Fig. 13: K-Map for Sum in Half-Adder
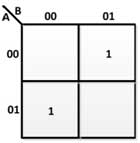
Fig. 14: K-Map for execution in Half-Adder
Therefore, the Boolean expressions for the Sum and Carry output are as follows –
SUM = A'B + AB' or SUM = A 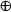 B
B
LOAD = AB
Therefore, the binary adder built in this project provides a sum with carry. This half adder has two inputs for the two bits to be summed and two outputs, one from the sum 'S' and the other from the transport 'c' to the highest adder position. In the half adder circuit, the transport signal for the addition of the least significant bits is taken from the output of the AND gate while the sum is taken from the output of the EX-OR gate.
Full adder
Full adder is a combinational circuit that forms the arithmetic sum of the input. It consists of three inputs and two outputs. A full adder is useful for adding three bits at a time, but a half adder cannot do this. The full adder has the following truth table –
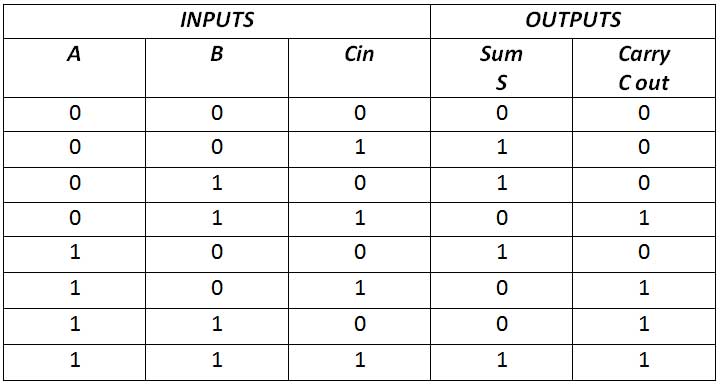
Fig. 15: Full Adder Truth Table
From the above truth table, the following K maps are drawn to derive the Boolean expressions for the sum and carry output –
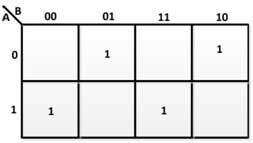
Fig. 16: K-Map for Sum in Full-Adder
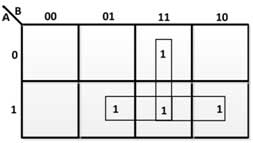
Figure 17: K-Map for Full-Adder execution
Therefore, the Boolean expressions for the Sum and Carry output are as follows –
SUM = A'B'C + A'BC' + ABC
= A'(B'C 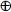 BC') + A(BC')
BC') + A(BC') 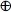 B.C)
B.C)
= A'(B 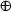 C) + A ( B
C) + A ( B 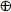 W )
W )
= A 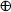 B
B 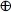 W
W
LOAD = A'BC + ABC + ABC' + AB'C
= AB + A'BC + AB'C
=AB + C(A 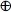 B )
B )
= AB + BC + AC
Half Subtractor
The half subtractor is constructed using X-OR and AND gates. The half subtractor has two inputs and two outputs. The outputs are difference and loan. The difference can be applied using the X-OR gate, the borrow output can be implemented using an AND gate and an inverter. The half subtractor has the following truth table –
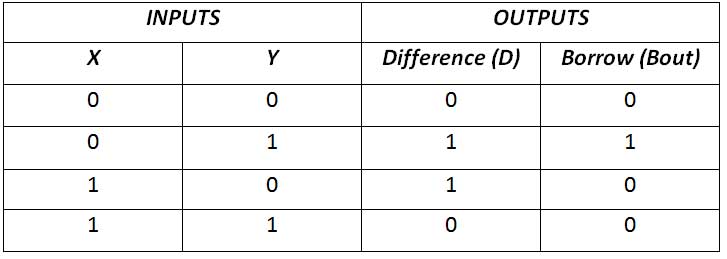
Fig. 18: Half Subtractor Truth Table
From the above truth table, the following K-maps are drawn to derive the Boolean expressions for the difference and the borrowed output –
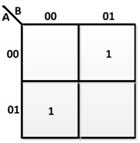
Figure 19: K-Map for difference in half subtractor
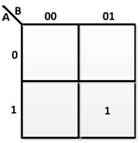
Figure 20: K-Map for loan in half subtractor
Therefore, the Boolean expressions for output of Difference and Loan are as follows –
DIFFERENCE = A'B + AB'
LOAN = A'B
Complete Subtractor
The full subtractor is a combination of X-OR, AND, OR, NOT gates. In a complete subtractor the logic circuit must have three inputs and two outputs. The two half subtractors together give a full subtractor. The complete subtractor has the following truth table –
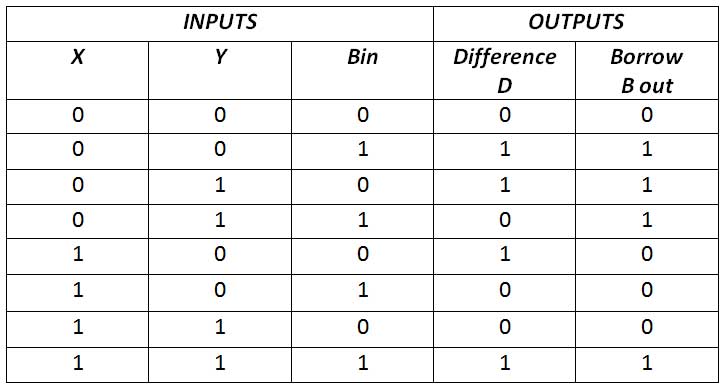
Fig. 21: Complete Subtractor Truth Table
From the above truth table, the following K-maps are drawn to derive the Boolean expressions for the difference and the borrowed output –
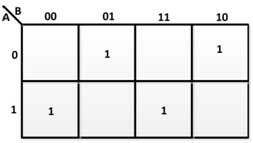
Figure 22: K-Map for difference in full subtractor
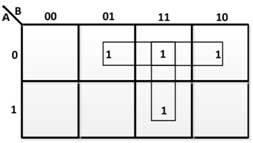
Figure 23: K-Map for full subtractor loan
Therefore, the Boolean expressions for output of Difference and Loan are as follows –
DIFFERENCE = ONE 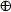 B
B 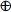 W
W
LOAN = A'B + BC + A'C
Testing the circuits –
The above designed combinational circuits can be tested by supplying supply voltage to the ICs by a battery through 7805 voltage regulator. The same voltage can be reduced to 2V level using a variable resistor for logic HI while supplying logic LOW through the Earth. The output signals can be checked by connecting LEDs to the output pins of each combinational circuit. Circuits can be verified by checking the truth tables for each circuit.
In the next tutorial, learn about code converter circuits.
Circuit diagrams
| Complete Adder-Circuit Diagram | 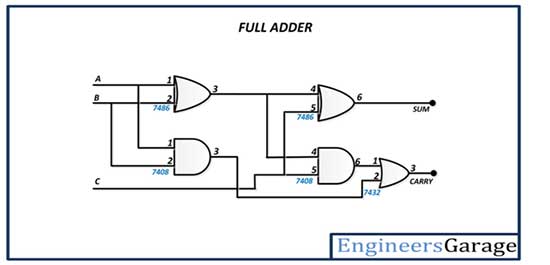 |
| Complete Circuit-Subtractor Diagram | 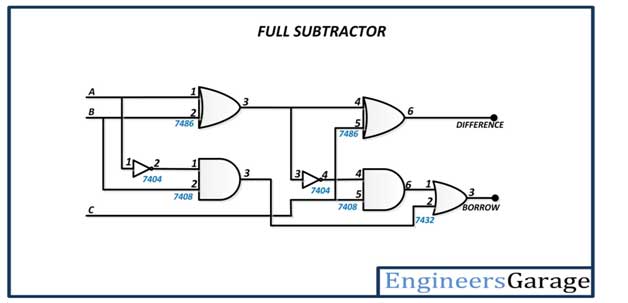 |
