We have already learned about the different components that make up an industrial robot or a robotic arm. We also discuss different types of robots used in industry. One of the most important terms used in the context of robots and their design is degree of freedom. In this article we will talk about the degree of freedom in robots. Why is it so important and how is it calculated.
What is the degree of freedom?
The degree of freedom is an extremely important factor in robotics, used to define the physical movement capabilities of a robot. A robot is essentially a combination of multiple mechanisms where each mechanism is made up of a set of links and joints. As already discussed, there are different types of joints used in the construction of a robot. The most common bottom pair joints include the revolution joint, prismatic joint, helical joint, cylindrical joint, spherical joint and universal joint. Each joint has its own degree of freedom. Swivel, helical, and prismatic joints have 1 DoF, cylindrical and universal joints have 2 DoF, and spherical joints have 3 DoF. When the degree of freedom is determined for a joint, it generally refers to the number of axes that the joint provides movement to the attached links.
When multiple joints are connected to form a robotic arm or industrial robot, the resulting degree of freedom is different. In the context of a robot, the degree of freedom is the number of independent variables or parameters that define the robot's motion or configuration. DoF represents the number of ways a robot can move or position itself in its workspace. The greater the degree of freedom, the more flexible and adaptable the robot is. A robot with high DoF can perform more complex movements and perform a variety of tasks. A higher DoF, however, entails more costs, complexity, and control challenges.
How to calculate the degree of freedom of a robot?
Determining a robot's degree of freedom may not be so easy. For certain types of robots, it's quite simple. For example, a Cartesian robot is always 3-DoF. A scalar robot is 4-DoF. Although for other types of robots and robot designs, it's not that simple. If each joint of the robot is independent and has no constraints and dependencies, the total DoF of the robot will be the sum of the DoF of all joints. For example, if a robot has two revolute joints and two prismatic joints, all independent without any dependencies, the total DoF of the robot is 4 (2 + 2), with each joint adding one degree of freedom. Generally, the joints are not all independent and have some restrictions applied to them. Joint dependencies further complicate the equation.

Figure 1.
Each type of joint has a certain number of independent restrictions. For example, the number of independent constraints between two planar rigid bodies for revolute and prismatic joints is 2. The number of independent constraints between two spatial rigid bodies for revolute and prismatic joints is 5. The number of independent constraints between two rigid bodies space for helical, cylindrical, universal and spherical joints is 5, 4, 4 and 3, respectively. The degree of freedom of a specific joint is the difference between the number of independent restrictions and the sum of the freedoms of the bodies. By this calculation, swivel, helical, and prismatic joints have 1 DoF, cylindrical and universal joints have 2 DoF, and spherical joints have 3 DoF.
The degree of freedom of the independent joints is summarized in table 1 .
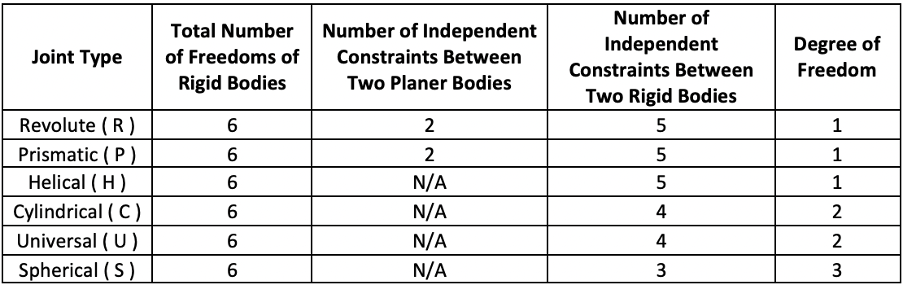
Table 1.
As each robot has a different mechanism, the calculation of the degree of freedom may be different. A common way of determining a robot's degree of freedom is the Kutzbach criterion and the Chebychev-Grubler criterion, known as the Grubler Formula. Kutzbach's criterion applies only to the degree of freedom of mobility of a flat mechanism. According to Kutzbach's criterion, for a planar or spatial mechanism to be mobile, that is, to have a degree of freedom greater than 0, the number of constraint equations (C) must be greater than or equal to the difference in the number of links (L) of the number of independent kinematic parameters (P).
C >= PL for any planar or spatial mechanism to be mobile.
According to the Chebychev-Grubler criterion, the degree of freedom of the mechanism is given by the following equation ( Equation 1 ).

Equation 1.
Where:
m = degrees of freedom of a single body/link, which is equal to 3 for a rigid body moving in a plane and is equal to 6 for a rigid body moving in three-dimensional space.
N = Number of links/bodies including earth
J = Number of joints
Ci = Number of constraints provided by joint i
fi = Number of freedoms provided by articulation i
When applying the Chebychev-Grubler criterion to a planar mechanism, the equation for DoF is:
DoF = 3(L-1) – 2J – H
Where:
L = Number of links
J = Number of binary joints
H = Number of highest pairs
Let us apply the Chebychev-Grubler criterion to some planar mechanisms that do not have superior pairs to calculate the degree of freedom.
For a closed-chain three-bar mechanism as shown in Figure 2 .
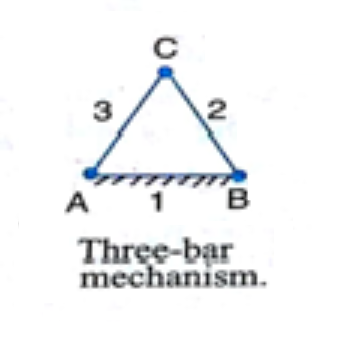
Figure 2.
DoF = 3(3-1)-2×3 = 0
For a four-bar closed chain mechanism as shown in Figure 3 .
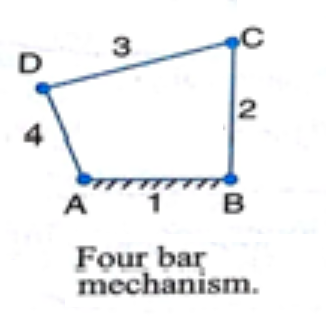
Figure 3.
DoF = 3(4-1)-2(4) = 1
For a five-bar closed-chain mechanism, as shown in Figure 4 .
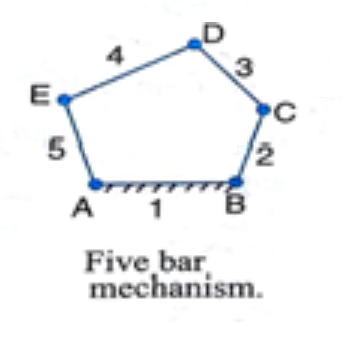
Figure 4.
DoF = 3(5-1)-2(5) = 2
For a five-bar closed chain mechanism with two ternary joints, as shown in Figure 5 .
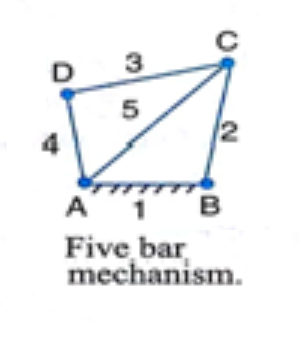
Figure 5.
DoF = 3(5-1)-2(6) = 0
For a closed six-bar chain mechanism with four ternary joints, as shown in Figure 6 .
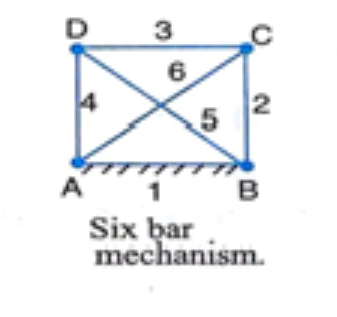
Figure 6.
DoF = 3(6-1) – 2(8) = -1
Grubler's Formula can only be applied to mechanisms that have 1 DoF joints, that is, the joints that form the robotic system are revolution, prismatic or helical. Does not apply to mechanisms with 2-DoF or 3-DoF joints. The formula can also be applied to open-chain mechanisms. For example, an open chain mechanism with 3 revolution joints and a prismatic joint is shown in Figure 7 .
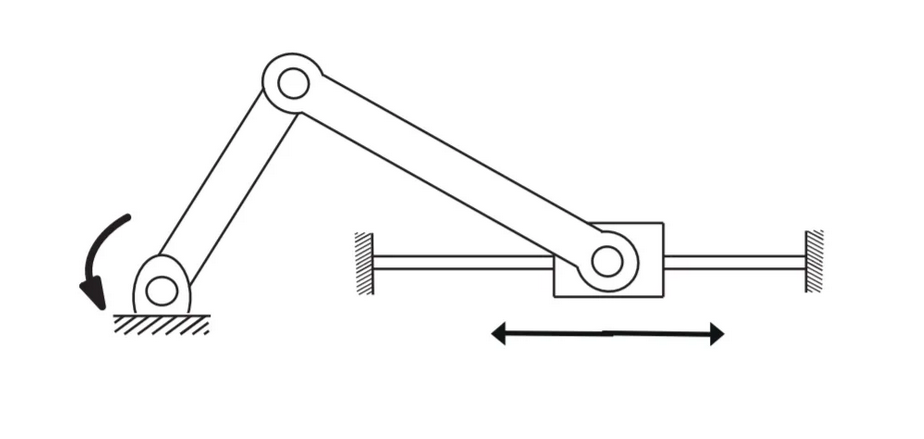
Figure 7. Open chain mechanism with 3 revolution joints and a prismatic joint.
There are four links/bodies connected by four joints, each joint having 1-DoF, so by Grubler's Formula
DoF = 3 (4-1-4) + (1+1+1+1) = 1
Grubler's Formula is not applicable when the joints are not independent. For example, consider the following mechanism.
By applying the Grubler equation to the above mechanism ( Figure 8 ), we obtain a DoF of 0.
Figure 8. Open chain mechanism with 3 revolution joints and a prismatic joint with the Grubler equation applied.
DoF = 3 (3-1-3) + (1+1+1) = 0
But it can be clearly seen that the above mechanism has a degree of freedom equal to 1. Since the intermediate joint in the above mechanism is not independent, Grubler's Formula does not apply to it.
Finding the degree of freedom for simple robot designs is easy, as there are more non-independent joints and more dependencies, determining the degree of freedom of a mobile robot becomes increasingly complex.
For simplicity, we can reduce most robotic mechanical designs into open-chain and closed-chain mechanisms, as shown in Figure 9 .
Figure 9.
As long as the robot has only 1-DoF joints such as revolution, prismatic and helical joints, the degree of freedom of the robot can be easily calculated using Grubler's Formula. As the robot involves non-independent joints, dependencies, and 2-DoF and 3-DoF joints, the calculations become more complicated.
Why is DoF important?
Each robot has a different mechanical structure. With the same links, a robot can be organized using different joints and in many ways. A robot's degree of freedom impacts many areas and plays a key role in defining the robot's performance. First, DoF determines the range and complexity of movements that a robot can perform. It is a key factor in deciding how robots will navigate and manipulate objects in different settings and work environments. A higher DoF robot can access and manipulate objects from many different angles and orientations, allowing it to perform more complex tasks.
Second, DoF is an important consideration in determining the adaptability of the robot to tasks. Different tasks require different ranges of motion, approach angles, and orientations. Simpler tasks can be accomplished by tasks with lower DoF, while more complex tasks require higher DoF. Furthermore, a robot's degree of freedom is again an important factor in determining the robot's workspace. A robot with a higher DoF not only has a larger workspace, but can also utilize the available workspace more efficiently. Therefore, the degree of freedom is important in determining the accessible workspace and the accessibility to objects in the accessible workspace.
The degree of freedom also determines the kinematic redundancy and redundancy resolution of the robot. The degree of freedom of a robot designed for an intended task should not be greater than necessary. Even unnecessarily high DoF can pose obstacles to a robot's movement, make it less energy efficient and impair its stability. The degree of freedom must be sufficient to increase the kinematic redundancy of the robot, so that the robot can effectively repeat movements in an energy-optimized manner while maintaining good stability and repeatability. The robot's design must be optimized so that its movement and posture match specific objectives.
A robot's degree of freedom also affects the robot's control and planning. As a robot's degree of freedom increases, more complex algorithms and control techniques are required to effectively plan, coordinate, and control multiple degrees of freedom. Planning and controlling a robot with multiple degrees of freedom involves facing challenges such as trajectory planning, trajectory generation, collision avoidance, and joint coordination.
Consequently, a robot's degree of freedom plays an important role in defining its range and reach, adaptability, repeatability, stability, performance, complexity, and efficiency.

