Design of metallic pillars according to EC3 – worked example

This article explains the design of steel columns according to Eurocode 3, EN 1993-1-1, using a practical example. Project explanations are made by referring to the relevant sections of the Code.

For a detailed explanation of the steel support structure, see the article Steel column design according to Eurocode 3 .

The design process described in the article above is as follows.

Let's start the design process with a practical example.

Design data

• Column dimensions 150x150x 31.1 kg/m
• Steel grade S275
• Column height 3m
• Axial load 500 kN
• For the sake of simplicity, in this example we consider the column with a pin end

Section classification

Let's find out the strength parameters.

t < 40mm

From Table 3.1 of EN 1993-1-1,

fy = 275 N/mm2

ε = √(235/f _j ) = √(235/275) = 0.92

From section 6.1:

γ _m0 = 1.0

γ _m1 = 1.0

H = 39.65cm ²

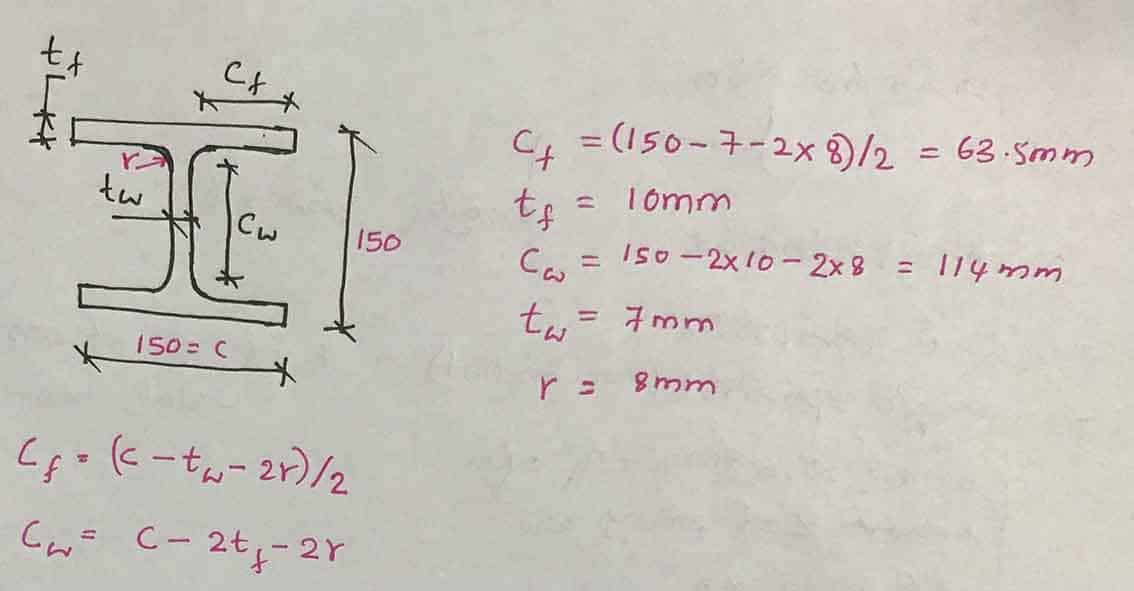
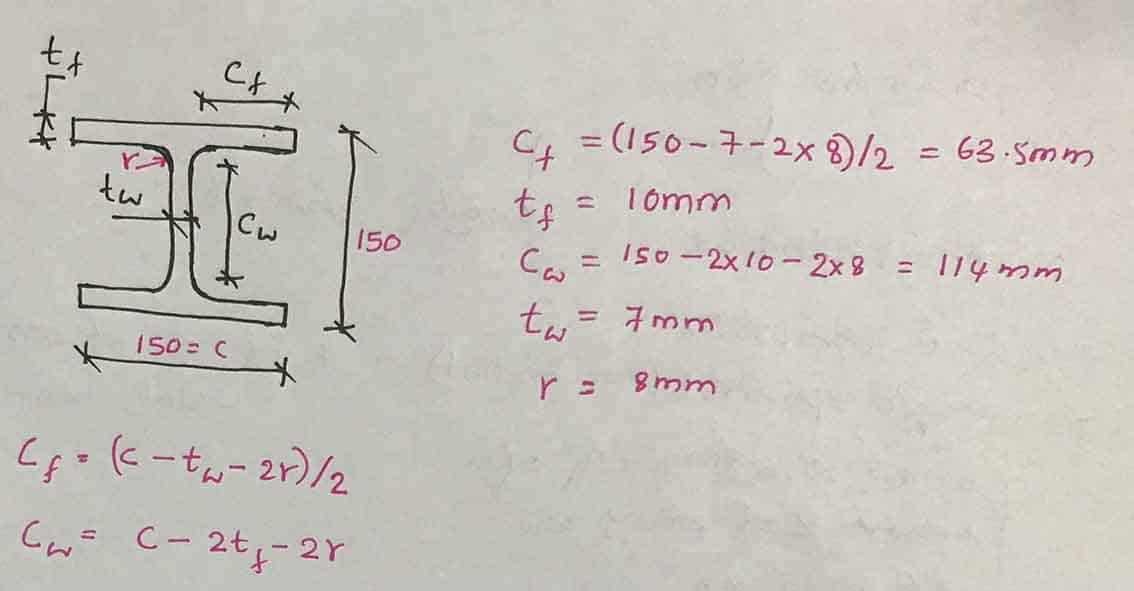
We can calculate thinness limits.

table

C _F /T _F = 63.5/10 = 6.35 < 9ε = 9 x 0.92 = 8.82; Class 1 section

network

C _i /T _i = 114/7 = 16.3 < 33ε = 33 x 0.92 = 30.36; Class 1 Section

• Plastic resistance or transverse resistance, N _{c, Road}
  • Non-thin profiles: Class 1

N _c,Rd = Af _j /γ _m0 = 3965 x 275/1 = 1,090.4 kN

After calculating the resistance, the following capacity test must be carried out.

N _Ed. = 500 kN

N _Ed. /N _c,Rd = 500/1090.4 = 0.46 <1

The cross section meets the plastic strength.

• Buckling resistance, N _{b, Road}

First calculate the buckling resistance depending on the section class.

Let's follow the procedure in the design process.

λ1 = 93.9ε = 93.9 x 0.92 = 86.4

When designing the pillar, we need to consider the resistance around each axis (YY and ZZ).

i = radius of gyration

EU _JJ = 6.4 cm

EU _currently = 3.77cm

M _cr = buckling length

Since the two ends of the column are fixed,

M _cr = 1.0 x L = 3m

λ¯ = I _cr / Iλ ₁

YY axis; λ¯ = L _cr / Lλ ₁ = 3000 / (64 x 86.4) = 0.54

ZZ axis; λ¯ = L _cr / Lλ ₁ = 3000 / (37.7 x 86.4) = 0.92

Let's determine the α – imperfection factor from Table 6.1 of EN 1993-1-1

Find the buckling curve

h/b = 150/150 = 1 < 1.2

T _F = 10 mm < 100 mm

Let's now look at part of table 6.2 of EN 1993-1-1,

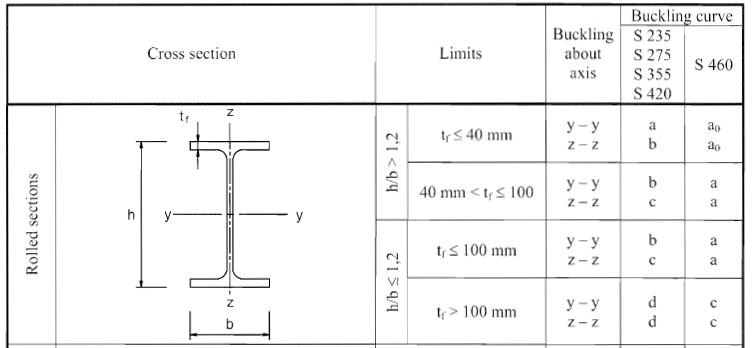
Therefore, the humpback curve results as follows

YY–b axis

ZZ–c axis

From Table 6.1

Bend Curve	To 0	A	B	W	D
Imperfection factor α	0.13	0.21	0.34	0.49	0.76

α on the YY axis = 0.34

α on the ZZ axis = 0.49

Now calculate Ø

Ø = 0.5 ( 1 + α( λ¯ – 0.2) + λ¯ ² )

About the YY axis

Ø = 0.5 (1 + 0.34(0.54 – 0.2) + 0.54 ² ) = 0.7

About the ZZ axis

Ø = 0.5 (1 + 0.49(0.92 – 0.2) + 0.92 ² ) = 1.1

Calculation of the reduction factor, χ

χ =1 /( Ø + √(Ø ² –λ¯ ² )) ≤ 1.0

About the YY axis

χ =1 /( 0.7 + √(0.7 ² – 0.54 ² )) = 0.873 < 1.0

About the ZZ axis

χ =1 /( 1.1 + √(1.1 ² – 0.92 ² )) = 0.587 < 1.0

The lower χ is the critical axis against buckling and lower buckling resistance is available.

Therefore,

χ = 0.587

Now calculate the buckling resistance N _{b, Road} ,

N _{b, Road} = χ A f _j /γ _M1 – Not thin – Class 1

N _{b, Road} = 0.587 x 3965 x 275/1 = 640 kN

• Capacity check

N _Ed. /N _{b, Road} ≤ 1.0

N _Ed. /N _{b, Road} = 500/640 = 0.781 <1

The section is ok.

For more information, see the article “Eurocode 3: Design and construction of metallic structures” published on Wikipedia.