Depending on the stress in the section, the sections are divided into compensation sections, above the reinforced section and below the reinforced section.
The section has certain areas of reinforcement, which are checked based on the development of deformations due to the applied loads. In other words, we check the capacity of the section taking into account the tension of the reinforcement and the tension of the concrete.
Before we get to the main topic, let's see how stress develops in the section subjected to bending stress.
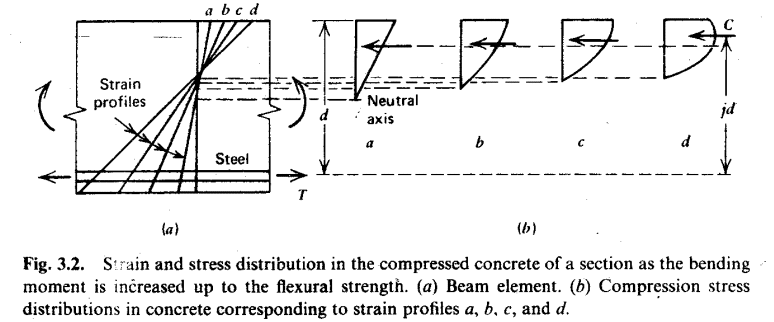
The following illustration from the book Reinforced Concrete Structures by Park and Paulay shows the development of stresses and deformations of a section.


The stress in the concrete gradually increases as the bending moment in the section increases. Finally, as the tension in the steel increases, it reaches its maximum load capacity.
The following figure shows the idealized compressive stress block under compression (from the same book).


Likewise, the variation of the amplified voltage can also be recorded.
Now let's take a look at the balanced, over-amped, and under-amped sections.
Let’s start with the “Balance” section.
Now calculate the strain development of the concrete section as per British standards.
Balance Section
In a state of equilibrium, the elongation of concrete and steel reaches its maximum value.
The following calculation can be used to determine the relationship between the neutral axis depth (x) and the effective depth (d). This calculation takes into account a simply reinforced section.


From the deformation diagram
x / (dx) = 0.035 / 0.002
x/d = 0.636
Therefore, when the intercept reaches x/d = 0.636, we call this an equilibrium state. Beyond this condition, the section fails as the load increases.
They say there is a balance error.
Let's look at the other two possible types of under-reinforced and over-reinforced sections. The different failure modes can be presented as follows.


Under reinforced section
As shown in the figure above, a section subject to tensile failure can be identified as being below the reinforced section.
At equilibrium, steel reaches its yield strength when the elongation is 0.002 and the elongation of concrete is 0.035. As the elongation increases further, the elongation of the steel reaches its maximum values, which leads to rupture of the reinforcement under tensile loads.
Cross-sectional failure due to reinforcement failure when reinforcement is inadequate is called under-reinforcement failure.
The maximum stress of the steel is called the tensile stress of the reinforcement. You can read the Tensile Strength of Reinforcement Bars article for more information about this type of error.
Furthermore, the simplified stress-strain diagram is taken into consideration during design.


As shown in the stress-strain diagram (BS 8110), the steel reaches its maximum stress f j /γ M (=460/1.15 = 400; for steel gate as per BS 8110-1985). After that, the stretch increases without increasing tension.
But the actual stress of Reinforced Steel increases, as discussed in the article Tensile Strength of Reinforcing Bars .
If the reinforcement reaches tensile strength and the concrete elongation is 0.0035 or less, the section will fail under tension in the under-reinforced state.
Most importantly, section failures under severe conditions provide clear warning signs of failure. Cracks in elements, excessive deformations, etc. are useful in understanding failures of this type.
Super reinforced section
Failure of the section under compression is called an overstrengthened condition. This is simply a failure of the concrete.
As we know, there are no warnings when concrete fails as it is a brittle failure. The designer must, therefore, take care to avoid failures of this type.
In the overamplified region, the following can be observed
- F S < f j The stress of the reinforcing elements is less than the yield strength of the reinforcing elements.
- The gain provided is less than that provided in the balanced state.
- The reinforcement does not yield and the concrete stress exceeds 0.0035.