In the previous tutorial, several Boolean postulates and theorems were discussed. These theorems and postulates are useful for deriving a Boolean expression. It was also discussed that for n number of variables, there can be at most 2^2n Boolean functions. Therefore, there can be a maximum of 16 (2^4) Boolean functions between two Boolean variables. A Boolean variable represents a singular binary data source in digital electronics, that is, a single bit or serial stream of bits. Therefore, there can be a maximum of 16 logic functions in digital circuits. Let's learn about all logical operations.
Fig. 1: Representational image of all Boolean logical operations
There can be 16 possible combinations of results between two Boolean variables, say X and Y. These results are shown in the following truth table –
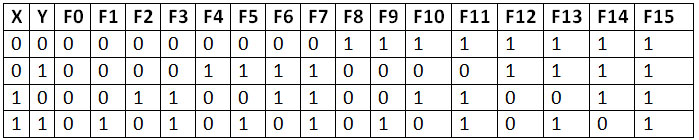
Fig. 2: Truth Table listing all possible Boolean functions for two variables
Corresponding to the following 16 possible outcome combinations, there are the following logical operations –
F0: Null – False output for all Boolean variable inputs is called Null. This is equivalent to the binary constant 0. The function is equivalent to the Boolean expression F = 0. Corresponding to the following 16 possible result combinations, there are the following logical operations –
F1:AND – The output being true when both boolean variable inputs are true otherwise the output being false is called AND operation. This is one of the basic logical operations. It is represented by the dot operator (.) in Boolean algebra. The function is equivalent to the Boolean expression F = xy or F = xy
F2: Inhibition – The output being true for one variable being true but the other not is called Inhibition. For function F2, the result is true as long as x is true but not y. In Boolean algebraic notation, it is written as x/y. The function is equivalent to the Boolean expression F = xy'.
F3: Transfer – The output being true if and only if one of the Boolean variables is true is called transfer. For function F3, the result is true as long as x is true independently of y. In Boolean algebraic notation, it is represented by simply writing x. The function is equivalent to the Boolean expression F = x.
F4: Inhibit – The output being true for one variable being true but the other not is called Inhibit. Function F4 is similar to function F2. For F4, the result is true as long as y is true but not x. In Boolean algebraic notation, it is written as y/x. The function is equivalent to the Boolean expression F = x'y.
F5: Transfer – The output being true if and only if one of the Boolean variables is true is called transfer. The F5 function is similar to the F3 function. For F5, the result is true as long as y is true independently of x. In Boolean algebraic notation, it is represented by simply writing y. The function is equivalent to the Boolean expression F = y.
F6: Exclusive-OR – The output being true only when one of the boolean variables is true but the other is not called exclusive OR. For this function, the result is true as long as either x or y is true, but not both. In Boolean algebra, the EX-OR operation is represented by 
operator . The function is equivalent to the Boolean expression F = xy ' + x'y .
F7: OR – The output being true if one or both of the Boolean variables are true is called OR operation. This is one of the basic logical operations. It is represented by the Plus (+) operator in Boolean algebra. The function is equivalent to the Boolean expression F = x + y.
F8: NOR – The inverse of the OR operation is called NOR. Your result is true only when both variables are false. In Boolean algebra, it is represented by the down arrow 
. Is written 
as . The function is equivalent to the Boolean expression F = (x + y)'.
F9: Equivalence – The output being true only when both variables are true or both are false is called equivalence. This is the inverse of EX-OR, which is why it is also called Exclusive NOR (EX-NOR). In Boolean algebra, it is represented as (x It is)'. The function is equivalent to the Boolean expression F = xy + x'y '.
F10: Complement – In the F10 function, the output is the complement of one of the Boolean variables. The result is true if y is false regardless of x. In Boolean algebra, it is represented as NOT of Y. It is written as y'. The function is equivalent to the Boolean expression F = y'.
F11: Implication – The output being true if one of the Boolean variables is false or the other is true is called implication. In Function F11, the output is true if y is false or x is true. In Boolean algebra, it is represented as x 
you. The function is equivalent to the Boolean expression F = x + y'.
F12: Complement – In the F12 function, the output is the complement of one of the Boolean variables. The result is true if x is false regardless of y. In Boolean algebra, it is represented as NOT of x. It is written as x'. The function is equivalent to the Boolean expression F = x'.
F13: Implication – The output being true if one of the Boolean variables is false or the other is true is called implication. In Function F13, the output is true if x is false or y is true. In Boolean algebra, it is represented as y x. The function is equivalent to the Boolean expression F = x' + y.
F14: NAND – The inverse of the AND operation is called NAND. It is one of the basic logical operations. The output of NAND is false if both boolean variables are true, otherwise it is true. In Boolean algebra, it is represented by the up arrow ( ). It is written as x y. The function is equivalent to the Boolean expression F = (xy)'.
F15: Identity – The true output for all Boolean variable inputs is called Identity. This is equivalent to the binary constant 1. The function is equivalent to the Boolean expression F = 1.
All possible logical operations between two Boolean variables are summarized in the following table –
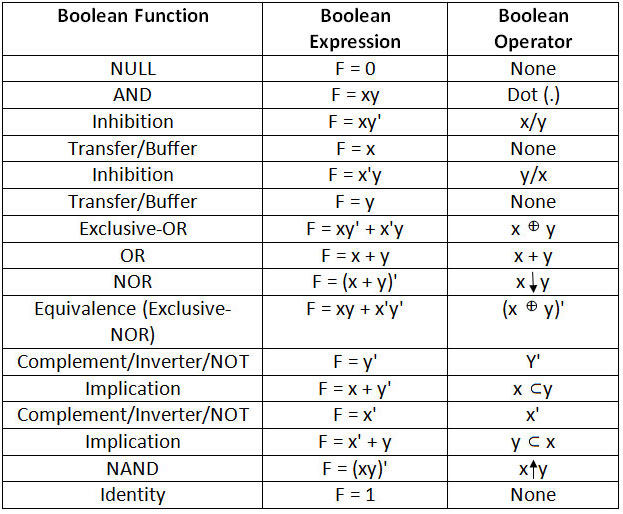
Fig. 3: Table listing all Boolean functions with two variables
Therefore, the basic logical operations – AND, OR, NOT, XOR, XNOR, NAND, NOR along with buffer, inhibit, implicate, null and identity operations are the only logical (Boolean) operations. Complement and transfer operations are unary operations that work on a single operand.
In the previous tutorial, a Boolean expression was minimized using truth table. But this is not a standard or systematic way to minimize a Boolean expression. In the next tutorial, learn about Gate Level Minimization which includes important mapping techniques for simplifying a Boolean expression. K-Map, VEM and QM techniques are important gate-level minimization techniques that must be known for implementing gate-level Boolean expressions and therefore digital circuits. Once gate level minimization techniques are known, practical digital circuits can be designed. Therefore, the basic logical operations – AND, OR, NOT, XOR, XNOR, NAND, NOR along with buffer, inhibit, implicate, null and identity operations are the only logical (Boolean) operations. Complement and transfer operations are unary operations that work on a single operand.
