La sección excesivamente reforzada se considera crítica en comparación con el estado insuficientemente reforzado. Si se refuerza demasiado, la sección puede fallar repentinamente y sin previo aviso debido a la rotura del concreto.
Sin embargo, en condiciones de ganancia insuficiente, la sección proporciona una advertencia más fuerte de falla.
Por lo tanto, el diseñador debe tener un buen conocimiento de estas condiciones, es decir, de equilibrio, bajo condiciones reforzadas y bajo condiciones reforzadas.
El artículo Equilibrio, sobreamplificación y subamplificación Para obtener más información sobre cada tipo y tipo de error, puede consultar.
Cabe señalar que las secciones demasiado reforzadas no fallan repentinamente. Fallan cuando el momento aplicado excede la capacidad de momento. Si el tramo falla, no habrá advertencias antes del fallo, como tramos insuficientemente reforzados.
La evaluación de la sección se lleva a cabo de acuerdo con las normas BS (BS 8110).
Este ejemplo trabajado verifica lo siguiente:
- ¿La sección está sobreamplificada?
- ¿Capacidad de momento flector de la sección sobrerreforzada?
Comprobemos esto con un ejemplo.
Mira la siguiente sección.
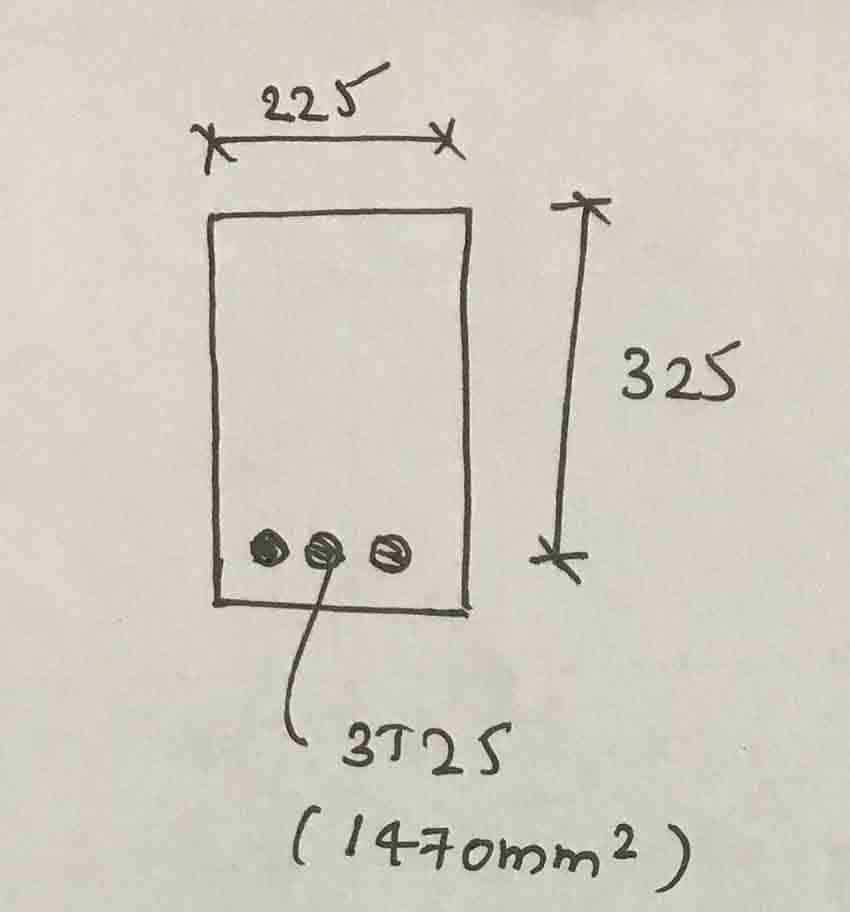

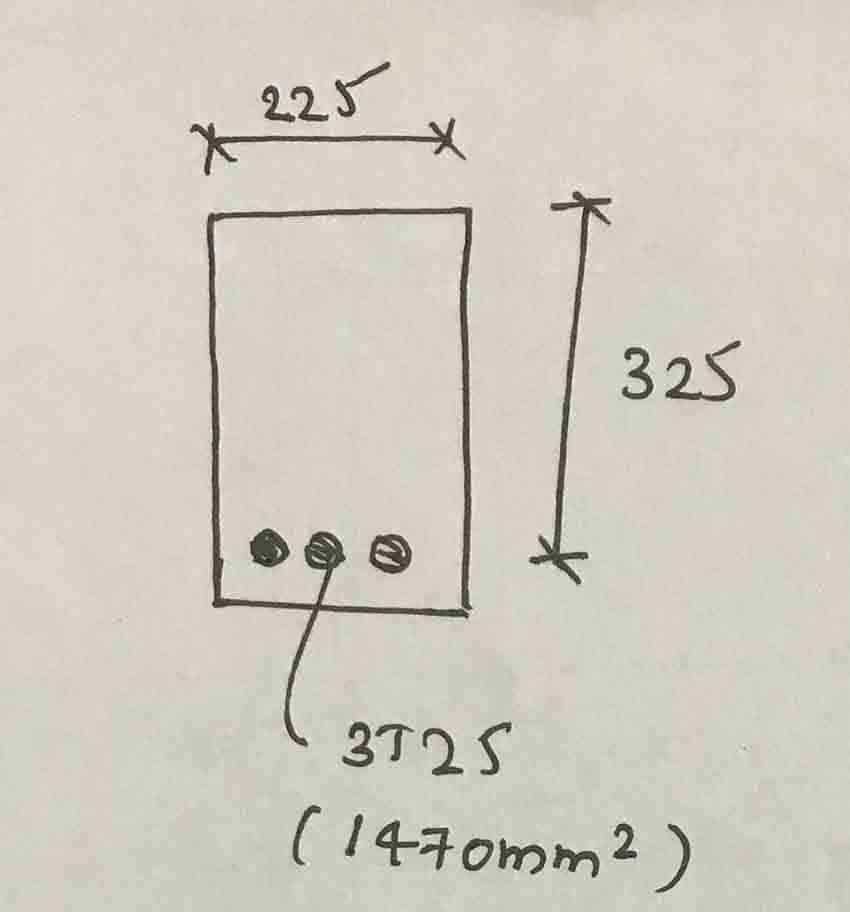
- Sección única reforzada
- Fcu = 25 N/ mm2
- fy = 460 N/ mm2
En este cálculo tenemos en cuenta la relación tensión-deformación básica de la sección transversal del hormigón.
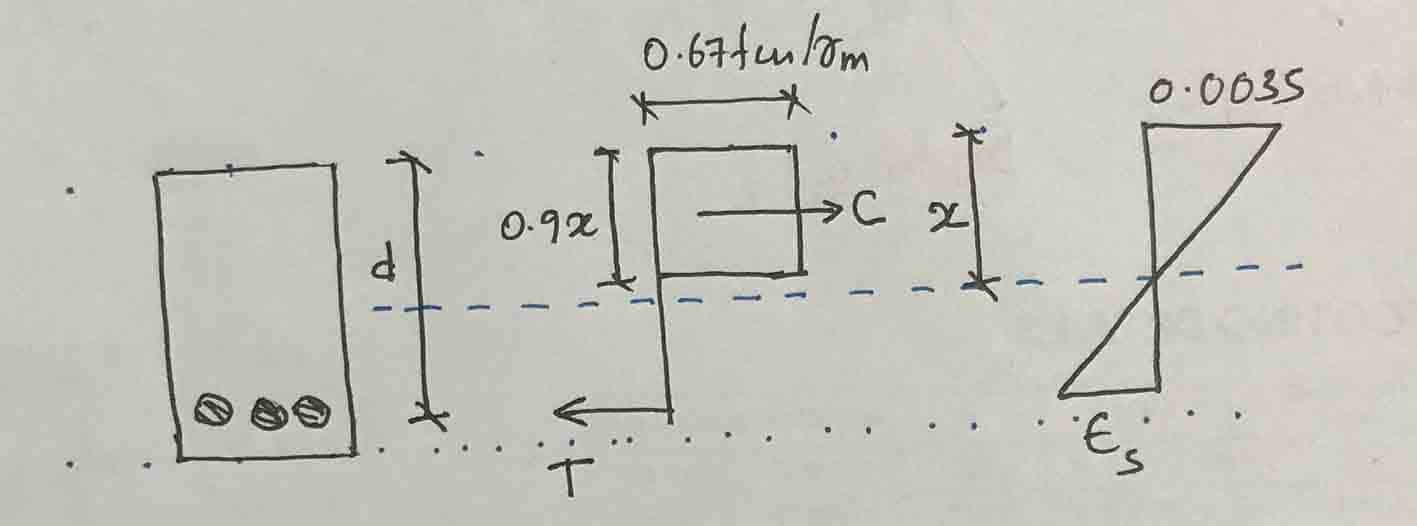
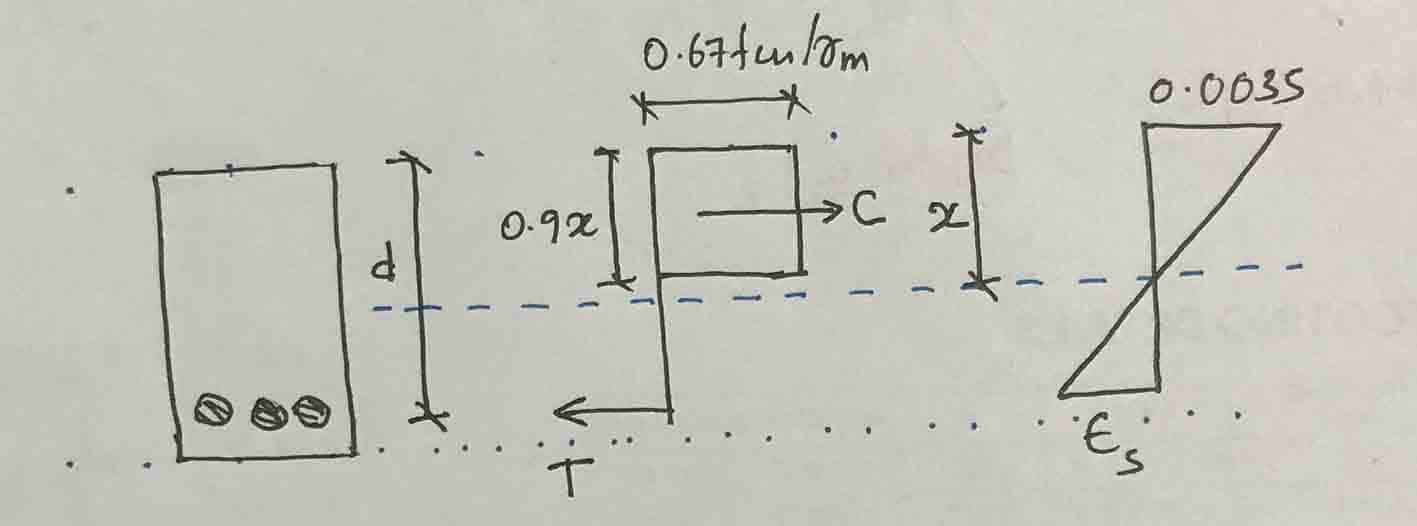
Primero supongamos que el refuerzo es retorno.
T = 0,87f j A S = 0,87 x 460 x 1470 = 588.294 N
C = (0,67f cu /ϒ M )(0,9x)b = (0,67×25/1,5)(0,9x)x225 = 226,125
C = T
226,125X = 588,294
x = 260 mm
x/d = 260/325 = 0,8 > 0,64
La sección está excesivamente reforzada.
La suposición de que el acero es duradero es incorrecta. Tenemos que descubrir la verdadera “x” mediante prueba y error. Esto debe hacerse hasta que C = T.
Supongamos que x = 225 mm
C = 226125 X = 226125 x 225 = 508781,25N
Ahora calcule la deformación del acero para encontrar la tensión del acero. La figura anterior se puede utilizar para calcular la deformación del acero.
εS = 0,0035(325-225)/225 = 0,0016
Ahora echemos un vistazo al diagrama tensión-deformación.
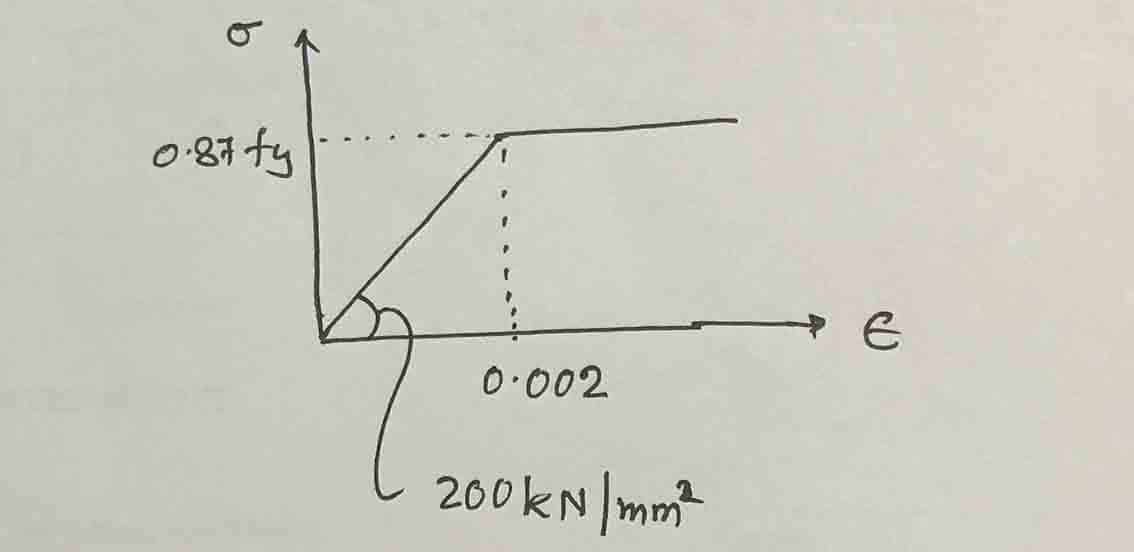
Tensión del acero, f S
F S = ε S E S = 0,0016 x 200×10 3 = 320 N/mm 2
T = 320 x 1470 = 470400N
C≠T
Necesitamos realizar varios experimentos hasta que C = T asumiendo diferentes profundidades del eje neutro ( X ).
Existe otro método para determinar directamente la profundidad del eje neutro. Como el acero no está por debajo del límite elástico (fs < 400 N/mm), 2 = 0,87 × 460).
Calcular el alargamiento del acero, ε S
ε S / 0,0035 = (d – x) / x
ε S = 0,0035 (325 –x)/x
Ahora calcula la tensión del acero.
F S = ε S E S = (0,0035 (325 – x)/x) 200×10 3
T=f S A S = (0.0035 (325 – x)/x) 200×10 3 x 1470
C = (0,67f cu /ϒ M )(0,9x)b = (0,67×25/1,5)(0,9x)x225 = 2278,125
T=C
(0,0035 (325 – x)/x) 200×10 3 x 1470 = 2278,125
X2 + 451,69x – 146798,35 = 0
x = 218,91 o -679,6; x debe ser positivo
Por lo tanto x = 218,91 mm
Ahora calcule la capacidad de flexión de la sección.
C = 2278,125 x 218,91 = 498704,34
Brazo de palanca
Z = d – 0,45x = 325 – 0,45 x 218,91 = 226,49 mm
M = Cz = 498704,34 x 226,49/10 -6 = 112,95 kN·m
La capacidad de momento flector de la sección sobrerreforzada es de 112,95 kNm.
Puede encontrar información al respecto en el artículo de Wikipedia “Hormigón armado”.