El método de construcción de vigas de torsión se explica en este artículo mediante un ejemplo práctico. Se deben seguir los mismos pasos básicos que para el diseño del refuerzo de vigas longitudinales.
El dimensionamiento de vigas para torsión calcula el requisito de adherencia torsional y un área adicional de refuerzo que se debe agregar al refuerzo longitudinal.
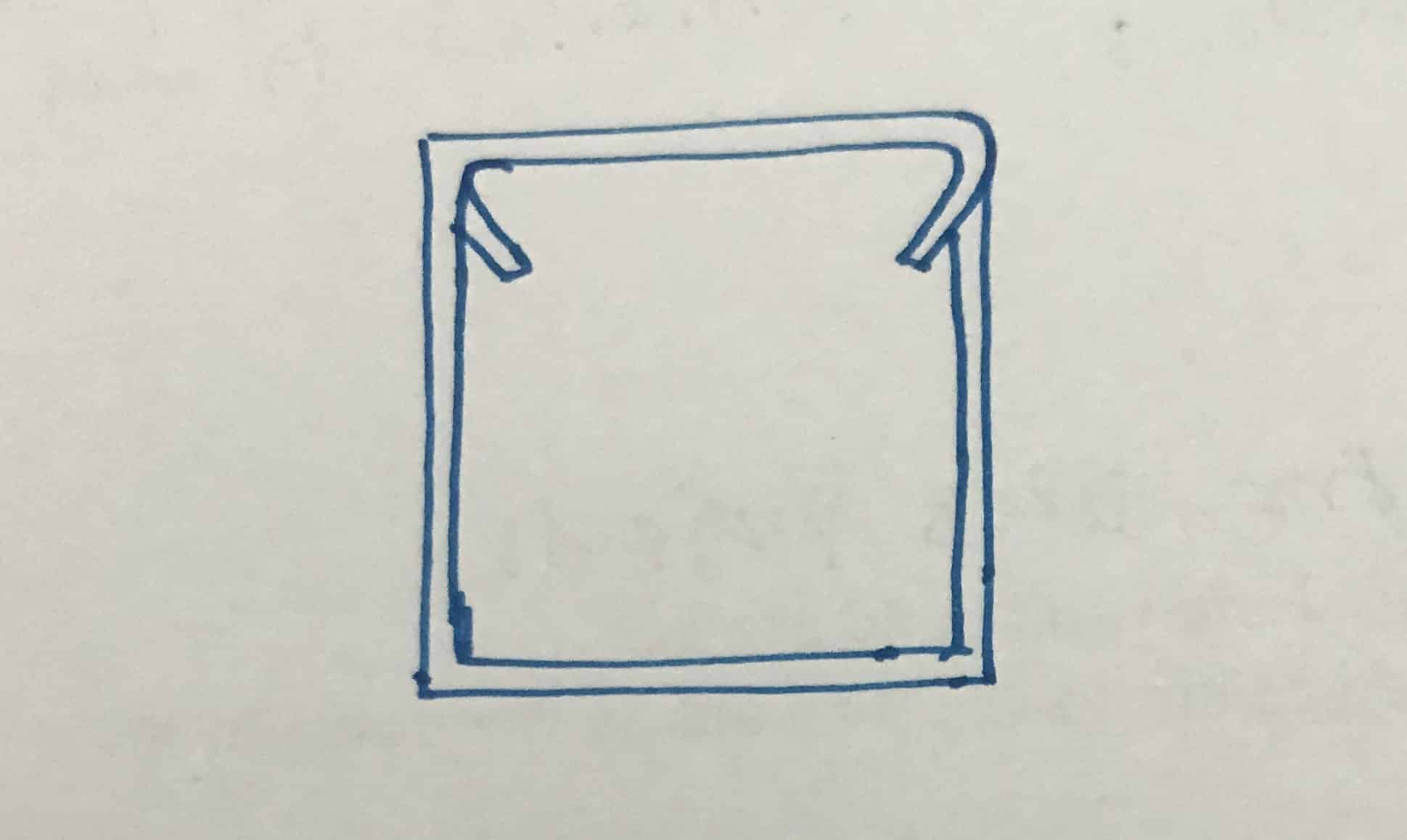
Lo más importante es que los miembros de refuerzo torsional no son los mismos que los enlaces de corte habituales destinados a vigas. Los enlaces de torsión terminan en dos extremos, a diferencia de los enlaces conversacionales.
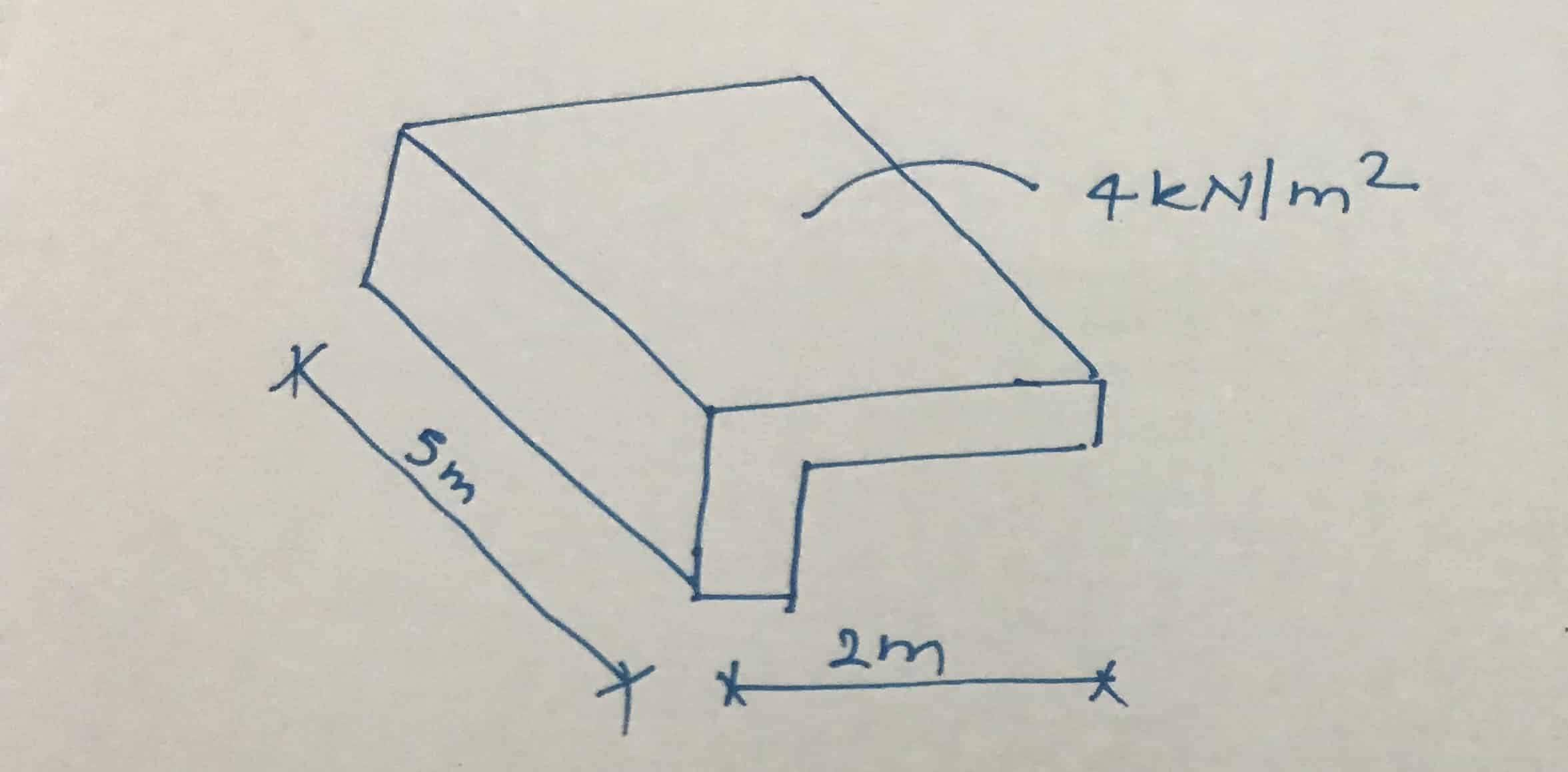
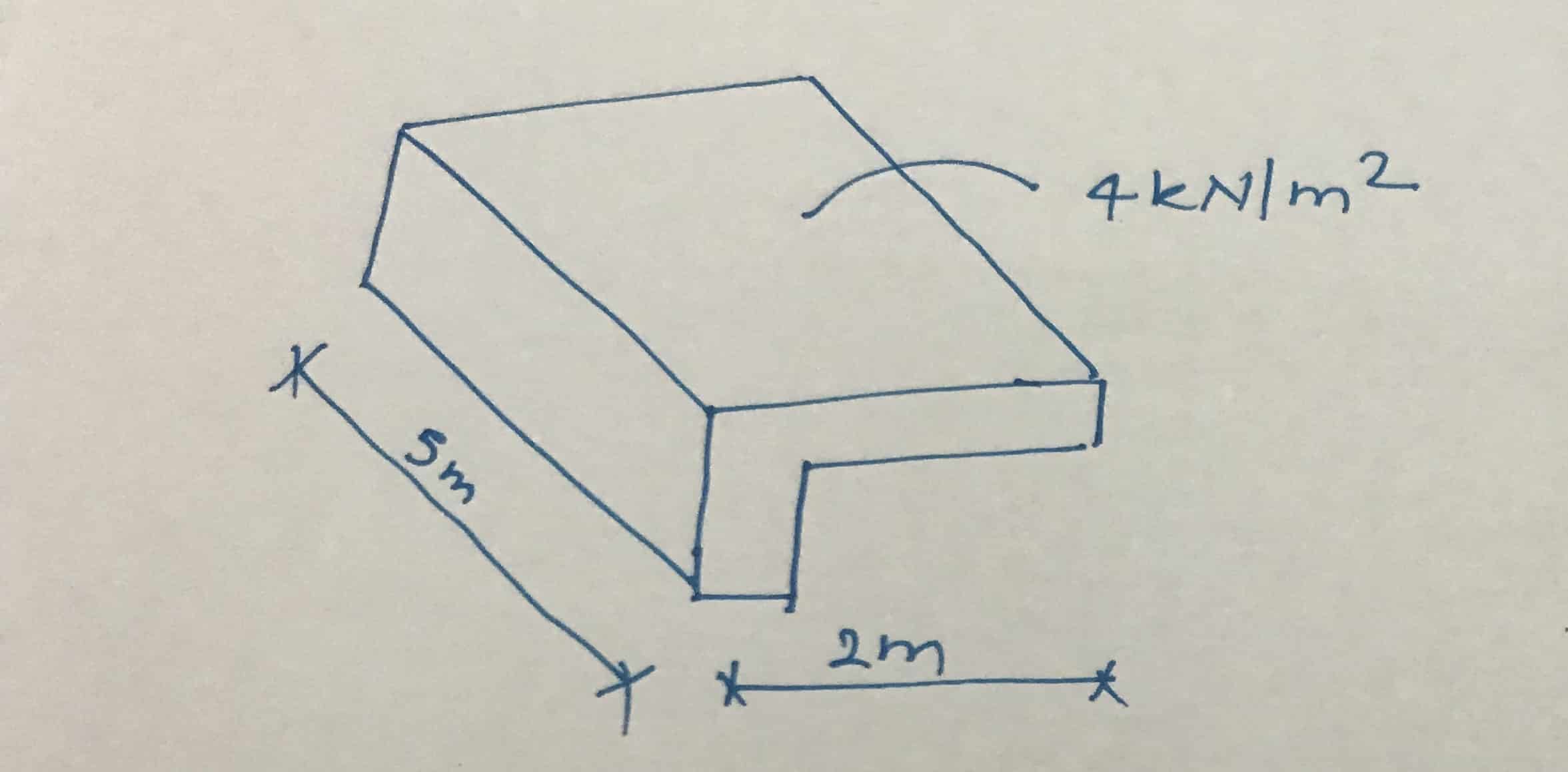
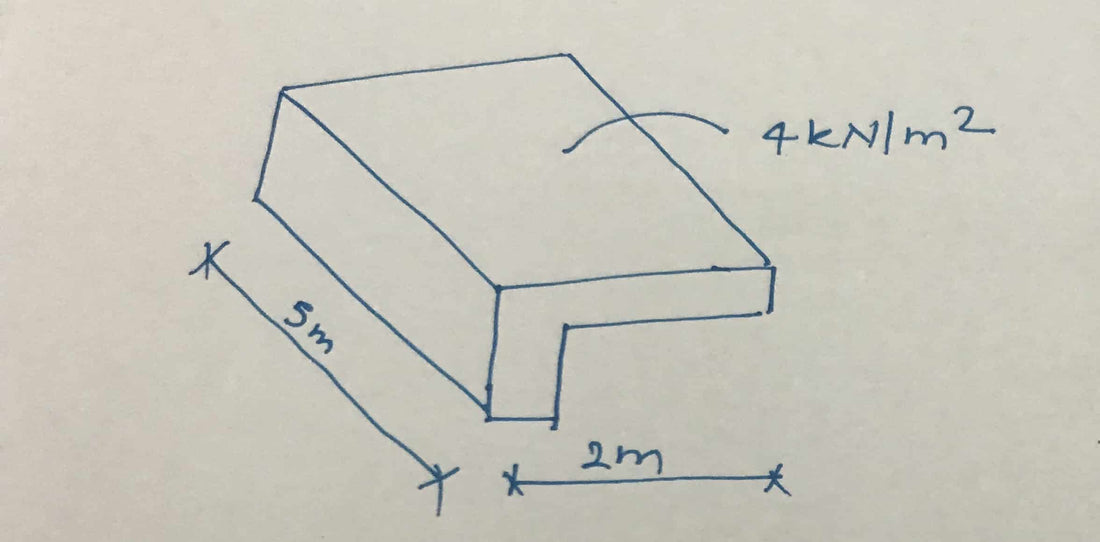
Ejemplo resuelto para el diseño de una viga de torsión.
- Luz de viga = 5m
- Envergadura del brazo voladizo = 2 m
- Altura del haz = 600 mm
- Ancho de haz = 300 mm
- Diámetro de conexión de corte = 10 mm
- Cobertura hasta refuerzo = 25mm
- Carga de diseño sobre la viga, incluidos todos los factores de carga = 4 kN/ m2
- Grado de hormigón C30
- Límite elástico característico = 460 kN/m 2
Cálculo del momento flector torsional.
Momento flector = 4 x 2 x 5 = 40 kNm
Momento flector por apoyo = 40/2 = 20 kNm
Cálculo del esfuerzo cortante torsional, v T
contra T = 2T/(h Mínimo 2 (H Máx -H Mínimo /3))
T = 20 kNm, h Mínimo = 300, h Máx = 600
contra T = 2x20x10 6 / (300 2 (600 – 300/3)) = 1,24 N/mm 2
De la Tabla 2.3 de BS 8110 Parte 2,
contra comino = 0,36 N/mm 2 y V u = 4,38 N/mm 2
contra el comino
En este ejemplo, no diseñaremos la viga para corte y flexión. Sin embargo, para este diseño necesitamos conocer el esfuerzo cortante y la capacidad cortante de la viga. Entonces supongamos algunos valores para el esfuerzo cortante.
Digamos v = 0,25 N/mm 2 y V contra C
Según los requisitos de refuerzo de corte y torsión, hay dos segmentos en la viga.
- contra T ≤v comino Los refuerzos nominales a cortante son suficientes y no es necesario diseñar la viga para torsión.
- contra T >v comino Diseño para eslabones de tijera de torsión.
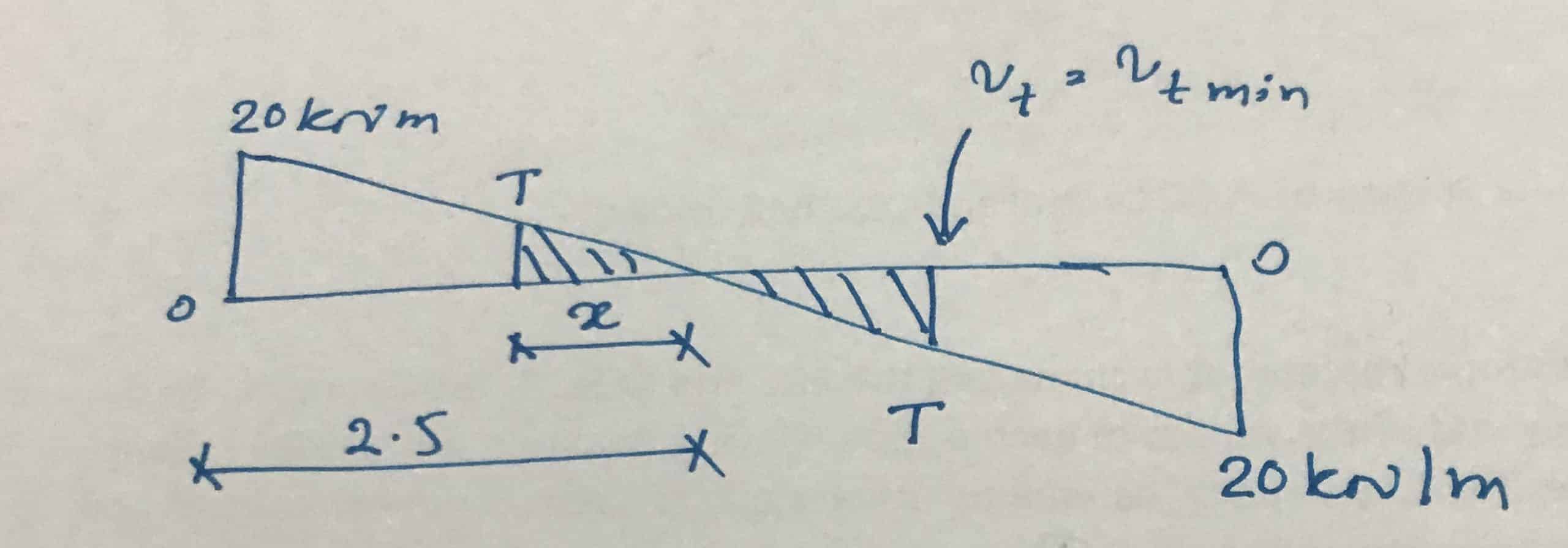
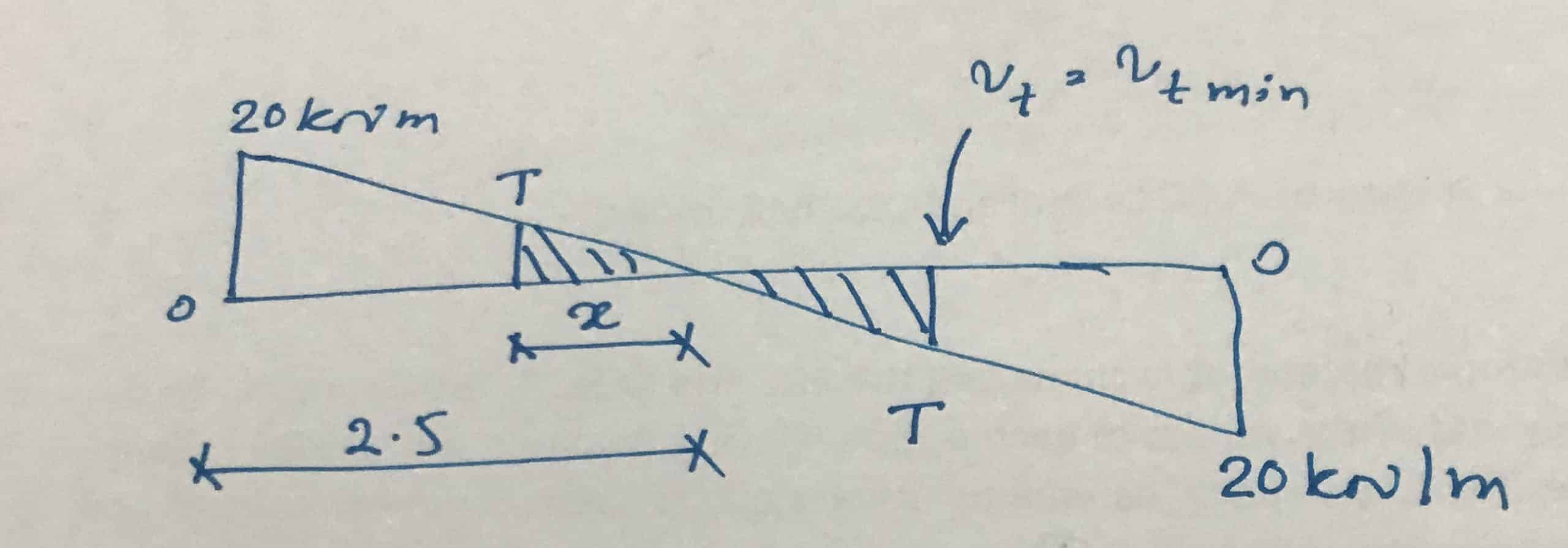
Podemos calcular fácilmente el segmento ya que solo necesitamos las conexiones de corte nominales.
Primero calculemos el momento de torsión, que determina el requisito mínimo para las barras de torsión.
T = v comino H Mínimo 2 ((H Max -H Mínimo /3))/2
T = 0,37 x 300 2 ((600 – 300/3))/2 = 8,33 kNm
Ahora calculemos la distancia hasta este momento.
Supongamos que es x.
x = (8,33/20) x 2,5 = 1,0m
Por este motivo, las uniones torsionales deben preverse a una distancia de hasta 1,5 m de cada soporte.
Cálculo de conexiones nominales de corte.
A SV /p versus ≥ 0,4b/0,95f jv
Considere barras T10 = 78 x 2 = 157 mm 2 * dos patas, por lo tanto el área de refuerzo se multiplica por 2; (78×2).
S contra ≤ 157 x 0,95 x 460 / (0,4 x 300) = 575 mm
Proporcione un espacio nominal entre juntas de corte de T10 a 250 mm. Esto también cumple con los requisitos mínimos para conectores de corte.
Cálculo del refuerzo de torsión.
A SV /p contra =T/(0.8x 1 j 1 (0.95f jv ))
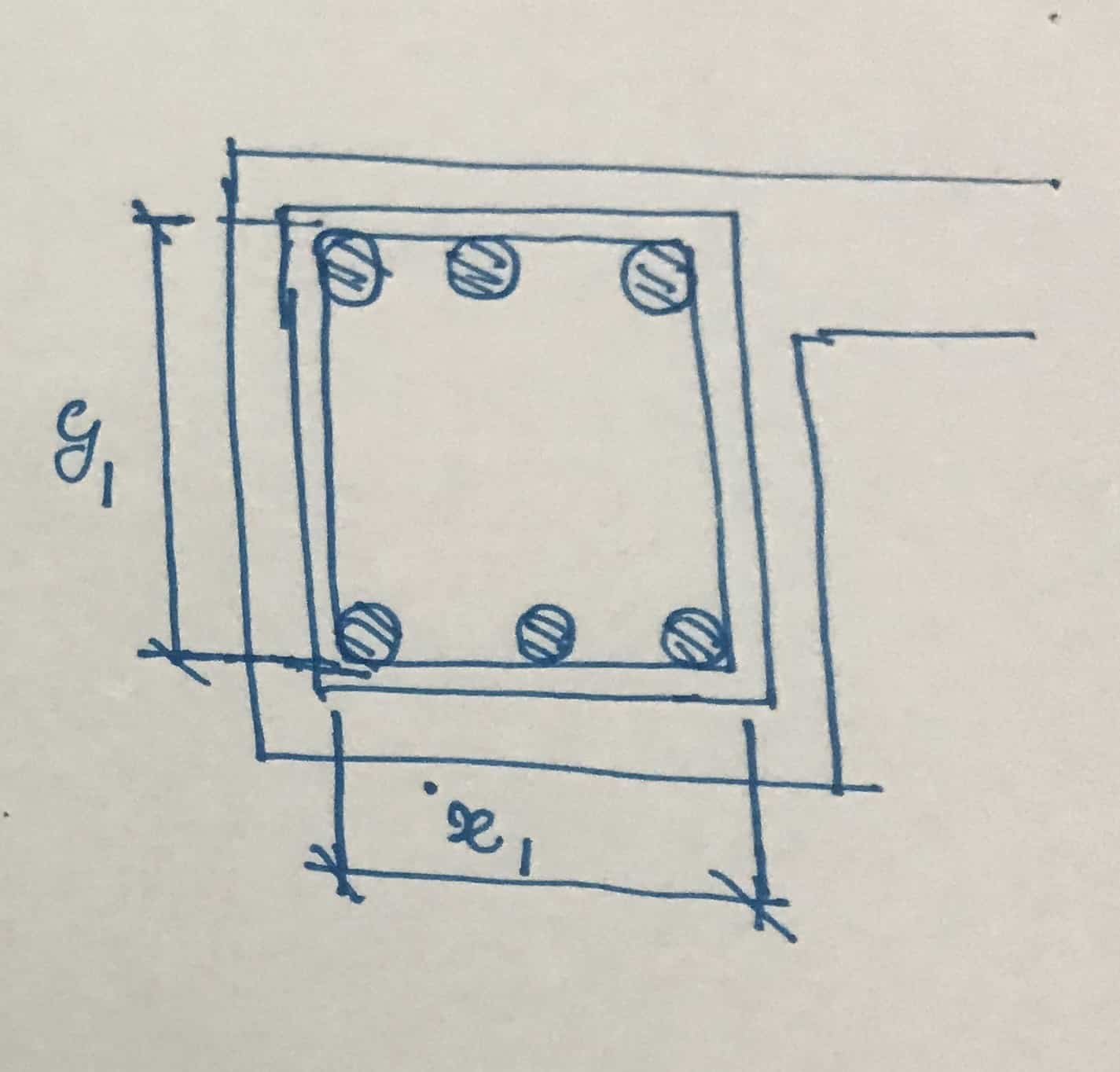
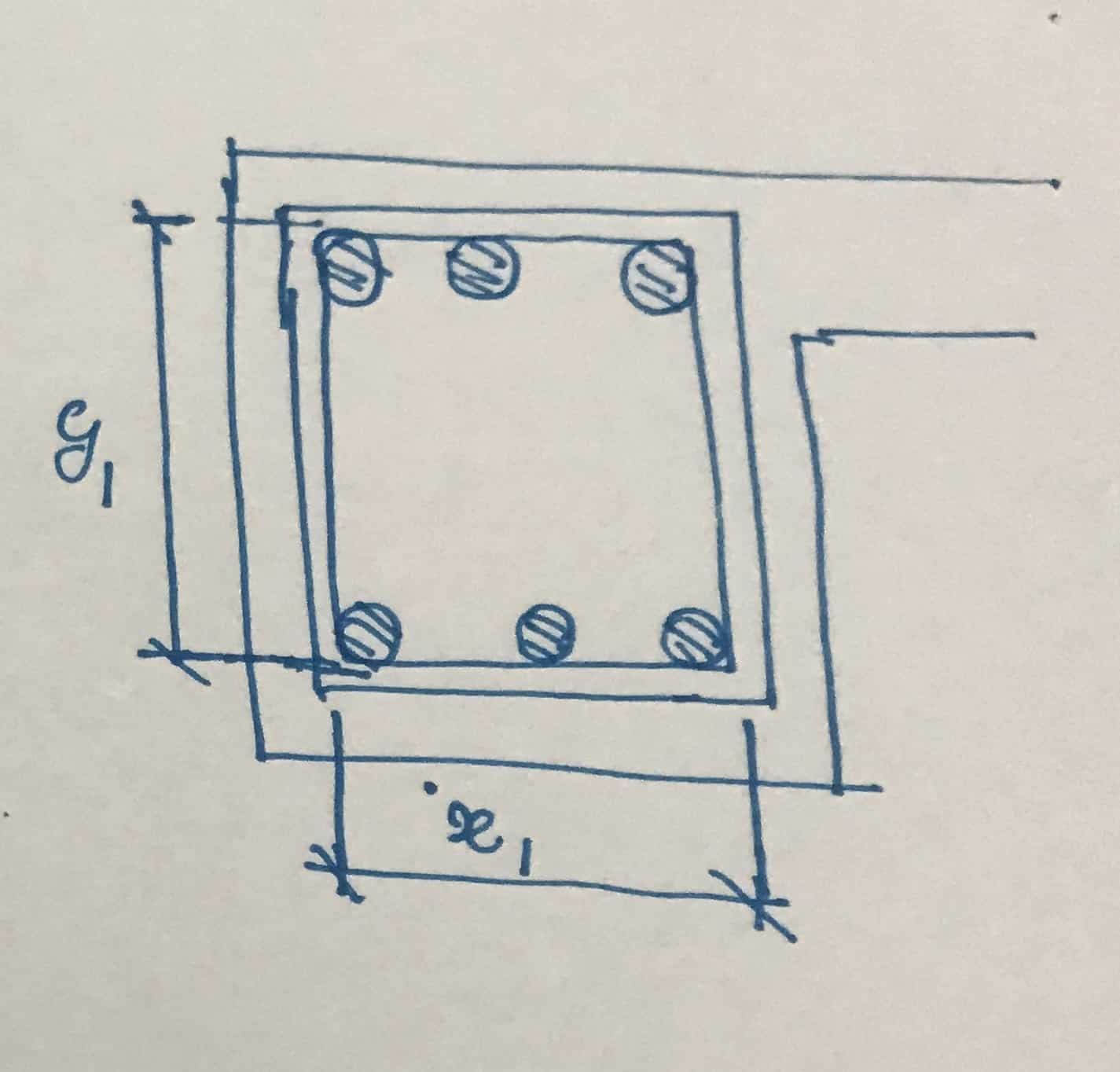
X 1 = Distancia central más corta de las conexiones de corte
X1 = 300 – 25 – 10/5 = 230 mm
X 1 = Distancia central más grande de las conexiones de corte
X1 = 600 – 25 – 10/5 = 530 mm
S contra ≤ 157 x 0,8 x 230 x 530 x 0,95 x 460 = 334 mm
Proporciona refuerzo de torsión, eslabones de tijera de torsión T10 con espacio de 200 mm.
Cálculo de refuerzo longitudinal adicional.
Se puede utilizar la siguiente ecuación de BS 8110 Parte 2.
A S = ON SV F jv (X 1 +s 1 )) /p contra F j
A S = 157 x 460 (230 +530)) / (334 x 530) = 358 mm2
Esta zona de refuerzo debe distribuirse en la parte superior, media e inferior.
Dado que el ancho de la viga es de 300 mm, podemos colocar tres vigas en la parte superior, dos en el medio y tres en la parte inferior. Esto da como resultado 8 compases.
Área de una barra = 358/8 = 44,7 mm 2
Podemos añadir esta zona de refuerzo a cualquiera de las tres barras superiores e inferiores. En el medio podemos ofrecer el 2T12.
Además, debemos comprobar la distancia máxima de la viga de torsión de 300 mm y asegurarnos de que haya refuerzo de torsión en las cuatro esquinas.
Además, debemos recordar que la unión por torsión no es lo mismo que la unión por corte normal.