Statement of the theorem
This theorem applies to linear and two-sided networks. Let's see what the phrase means.
In any complex network of multiple sources containing linear bilateral elements, the voltage or current flowing through any aspect of the network is identical to the algebraic sum of the individual voltages or currents separately across or within that element of each source acting individually when all remaining elements references are replaced by their respective internal resistances.
Explanation of the superposition theorem
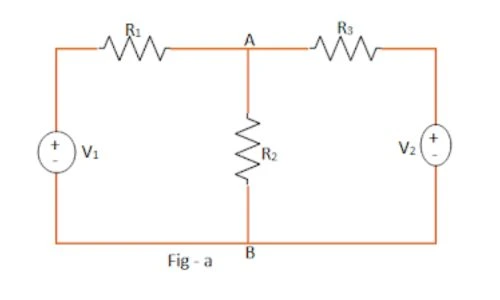
Step 1:
According to the superposition theorem, let us consider each source individually. Let's let the source V 1 Volts act independently. At this point, other authorities must be replaced by internal impedances.
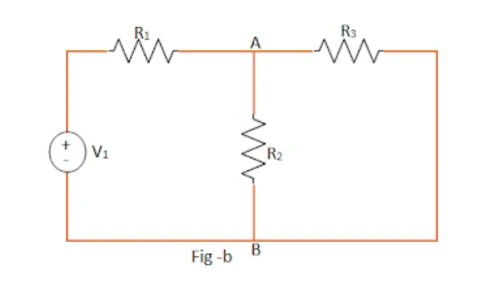
Step 2:
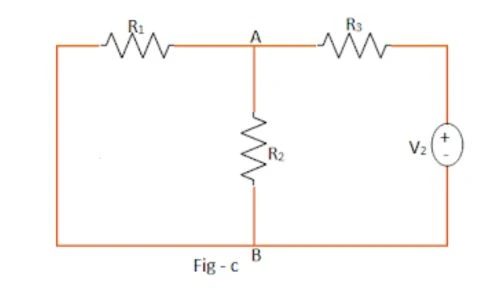
Step 3:
Steps to apply the superposition theorem
- Step 1 : Choose a single font that works alone. Short circuit other voltage sources and open power supplies if internal resistances are unknown. If known, replace them with your internal resistances.
- Step 2 : Find the current or voltage in the required element given the source under consideration using an appropriate network simplification technique.
- Step 3 : Repeat the above two steps for all sources
- Step 4 : Add the effects of each source to find the total current or voltage across the element.
Principles of the superposition theorem
The superposition theorem states that in a linear circuit with multiple sources (e.g., voltage and current sources), the response (voltage or current) at any point in the circuit can be found by considering the effect of each source individually and all other references must be defined. to zero. After analyzing each source individually, you can overlay or add the individual answers to find the overall answer.
This theorem is based on two fundamental principles:
- Linearity: The circuit must be linear, that is, the relationship between voltage and current in its components (resistors, capacitors, inductors, etc.) must be linear and obey Ohm's law. In other words, the behavior of the circuit should not change at different voltage or current levels.
- Overlap: Overlap assumes that the effects of individual sources are independent of each other. Therefore, you can analyze each source separately to determine the overall answer while zeroing in on all other benchmarks.
Assumptions and limitations
It is important to note that the superposition theorem has some limitations:
- Linear circuits only: The application of this theorem is limited to linear circuits; it cannot be used to analyze nonlinear components such as diodes or transistors.
- Independent sources: Sources must be independent of each other. This means that changing one source should not affect the behavior of the others.
- Time-invariant circuits: Circuit parameters, including resistance, capacitance, and inductance, should not change over time. In other words: the course must be time-invariant.
Procedure for applying the superposition theorem
To apply the superposition theorem, do the following:
- Turn off all independent voltage sources: Set all independent voltage sources to zero volts (replace with shorts). This effectively eliminates its influence on the price.
- Analyze the circuit: Analyze the history as you would for a single source, considering only the impact of the remaining sources (current and dependent sources).
- Determine the response: Calculate the desired response (voltage or current) of the circuit with only one active source.
- Repeat for each source: Repeat steps 1 through 3 for each independent authority in the circuit.
- Overlap the responses: Finally, add up all the responses obtained in Step 3 to find the total response of the circuit with all active sources.
Applications of the superposition theorem
The superposition theorem is widely used in electrical engineering and circuit analysis and finds application in several scenarios, such as:
- Network analysis: Simplifies the analysis of complex, multi-source electrical networks.
- Circuit structure: Engineers use superposition to optimize and design circuits, especially in cases where multiple sources interact.
- Transistor amplifier analysis: Engineers can use superposition to analyze the behavior of transistor amplifier circuits to improve their understanding.
- Power distribution systems: Power systems engineers can use the superposition theorem to analyze complex power distribution networks.
Conclusion
In summary, the superposition theorem proves to be an indispensable analytical tool that provides a systematic and powerful approach to dealing with the complexity of electrical circuits. By leveraging the principles of linearity and superposition, engineers gain a structured methodology for solving complicated problems and optimizing circuit designs. In addition to its applications in network analysis and circuit design, the superposition theorem is also useful for the analysis of transistor amplifiers and power distribution systems. As a fundamental concept in electrical engineering, the superposition theorem continues to assist researchers and professionals, which is crucial for understanding and designing electrical circuits. Its continued relevance underscores its position as an invaluable tool in the electrical engineer's toolbox.
Common questions
Can engineers apply the superposition theorem to circuits with nonlinear components?
No, engineers cannot apply the superposition theorem to nonlinear circuits. This theorem is explicitly designed for linear circuits, and the complexity introduced by nonlinear components such as diodes or transistors exceeds their capabilities. Engineers must use alternative analysis methods for circuits with nonlinear elements.
How does the superposition theorem treat time-varying circuits?
The superposition theorem assumes that circuit parameters, including resistance, capacitance, and inductance, remain constant over time. Time-dependent circuits in which these parameters change over time do not fall within the scope of the superposition theorem. Alternative techniques, such as Laplace transforms, may be more suitable for analyzing such circuits.
Can the superposition theorem be used in source-dependent circuits?
Although the superposition theorem deals primarily with independent sources, engineers can extend its application to circuits with dependent sources under certain conditions. The crucial step is to analyze each source independently, keeping the other references at zero. However, engineers must be careful and consider the specific characteristics of dependent sources to ensure the validity of their analyses.