Case One
Given away:
- Disc mass M=50 kg
- Disc diameter D=500 mm
- Maximum disc speed 60 rpm
Select servo motor and reduction gear, component diagram as follows:
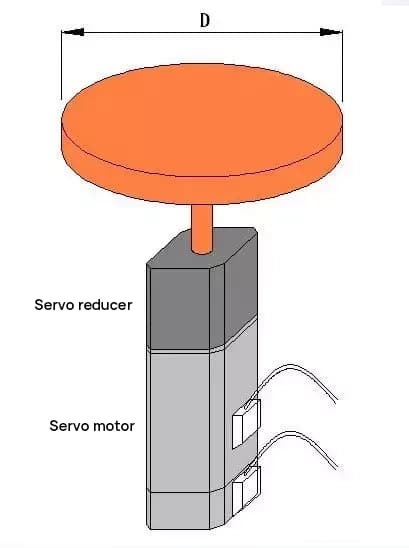
Calculation of the moment of inertia for disk rotation
J. l = MD 2 /8 = 50 * 50 2 / 8 = 15625 (kg cm 2 )
Assuming a gear reduction ratio of 1:R, the load inertia reflected on the servo motor shaft is 15625/R 2 .
According to the principle that the load inertia should be less than three times the rotor inertia J M of the motor,
if a 400 W motor is selected, J M = 0.277 (kg cm 2 ),
then: 15625/R 2 < 3*0.277,R 2 > 18803, R > 137,
the output speed = 3000/137 = 22 (rpm),
that does not meet the requirement.
If a 500 W motor is selected, J M = 8.17 (kg cm 2 ),
then: 15625/R 2 < 3*8.17,R 2 > 637, R > 25,
the output speed = 2000/25 = 80 (rpm),
that satisfies the requirement.
This type of transmission has minimal resistance, so torque calculations are ignored.
Case Two
Given away:
- Load weight M = 50 kg
- Synchronous belt wheel diameter D = 120 mm
- Reduction ratio R 1 = 10, R 2 = 2
- Coefficient of friction between load and machine table µ = 0.6
- Maximum load movement speed: 30 m/min
- Time for the load to accelerate from rest to maximum speed: 200ms
Ignoring the weight of each wheel on the conveyor belt,
What is the minimum power requirement for a motor to drive such a load?
The schematic diagram of the component is as follows:
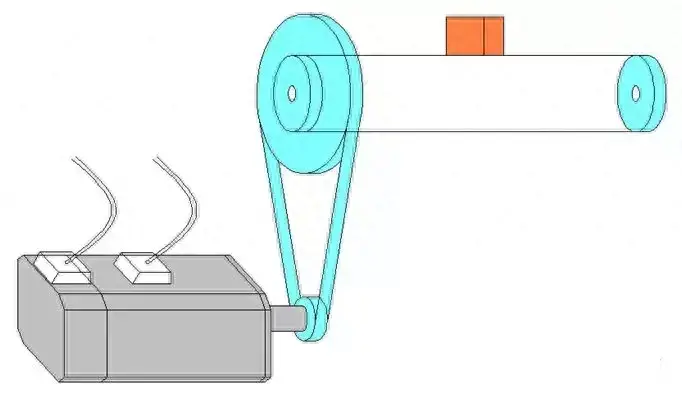
1. Calculation of the inertia of the load reflected on the motor shaft:
JL = M * D 2 /4/R 1 2
= 50 * 144/4/100
= 18 (kg cm 2 )
According to the principle that the load inertia should be less than three times the motor rotor inertia (JM):
J. M > 6 (kg cm 2 )
2. Calculation of the torque required to drive the engine load:
Torque required to overcome friction:
T f =M*g*µ*(D/2)/R 2 /R 1
= 50 * 9.8 * 0.6 * 0.06/2/10
= 0.882 (N·m)
Torque required for acceleration:
Ta = M * a * (D / 2) / R 2 /R 1
= 50 * (30/60/0.2) * 0.06/2/10
= 0.375 (N·m)
The nominal torque of the servo motor must be greater than T f and the maximum torque must be greater than T f +T a .
3. Calculation of required engine speed:
N = v / (πD) * R 1
= 30 / (3.14 * 0.12) * 10
= 796 (rpm)
Case Three
Given away:
- Load weight M = 200 kg
- PB screw pitch = 20 mm
- Screw diameter DB = 50 mm
- MB screw weight = 40 kg
- Friction coefficient µ = 0.2
- Mechanical efficiency η = 0.9
- Load movement speed V = 30 m/min
- Total movement time t = 1.4 s
- Acceleration and deceleration time t 1 = t 3 = 0.2s
- Rest time t 4 = 0.3s
Select the servo motor with the minimum power that meets the load requirements,
The component diagram is as follows:
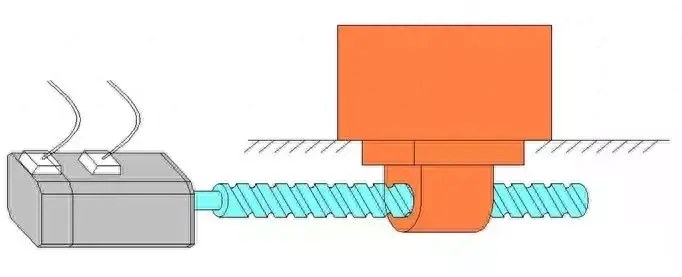
1. Calculation of Load Inertia Converted to the Motor Shaft
Load inertia of the weight converted to the motor shaft
J. C =M*(PB/2π)²
= 200 * (2/6.28)²
= 20.29 (kg·cm²)
The rotational inertia of the screw
J. B =M B *D B ²/8
= 40*25/8
= 125 (kg·cm²)
Total load inertia
JL = JW + JB = 145.29 (kg cm²)
2. Calculation of engine speed
Required engine speed
N=V/PB
= 30/0.02
= 1500 (rpm)
3. Calculation of the torque required to drive the motor load
The torque required to overcome friction
T f =M*g*µ*PB/2π/η
= 200*9.8*0.2*0.02/2π/0.9
= 1.387 (N·m)
Torque required when weight is accelerating
T A1 =M*a*PB/2π/η
= 200 * (30/60 / 0.2) * 0.02 / 2π / 0.9
= 1.769 (N·m)
Torque required when screw is accelerating
T A2 = JB * α / η
=J B *(N*2π/60/t 1 ) /η
= 0.0125 * (1500 * 6.28/60/0.2)/0.9
= 10.903 (N·m)
Total torque required for acceleration
T A =T A1 +T A2 = 12.672 (N·m)
4. Servo Motor Selection
Servo motor rated torque
T > T f and T > Trms
Servo motor maximum torque
T max. >T f +T A
Finally, the ECMA-E31820ES engine was selected.