Este artículo explica el diseño de columnas de acero según el Eurocódigo 3, EN 1993-1-1, mediante un ejemplo práctico. Las explicaciones del proyecto se realizan haciendo referencia a las secciones relevantes del Código.
Para una explicación detallada de la estructura de soporte de acero, consulte el artículo Diseño de columnas de acero según el Eurocódigo 3 .
El proceso de diseño descrito en el artículo anterior es el siguiente.


Comencemos el proceso de diseño con un ejemplo práctico.
Datos de diseño
- Dimensiones columna 150x150x 31,1 kg/m
- Grado de acero S275
- Altura de la columna 3m
- Carga axial 500 kN
- Para simplificar, en este ejemplo consideramos la columna con un extremo de pasador.
Clasificación de secciones
Averigüemos los parámetros de fuerza.
t < 40 mm
De la Tabla 3.1 de EN 1993-1-1,
fy = 275 N/mm2
ε = √(235/f j ) = √(235/275) = 0,92
De la sección 6.1:
γ m0 = 1,0
γm1 = 1,0
Un = 39,65 cm 2
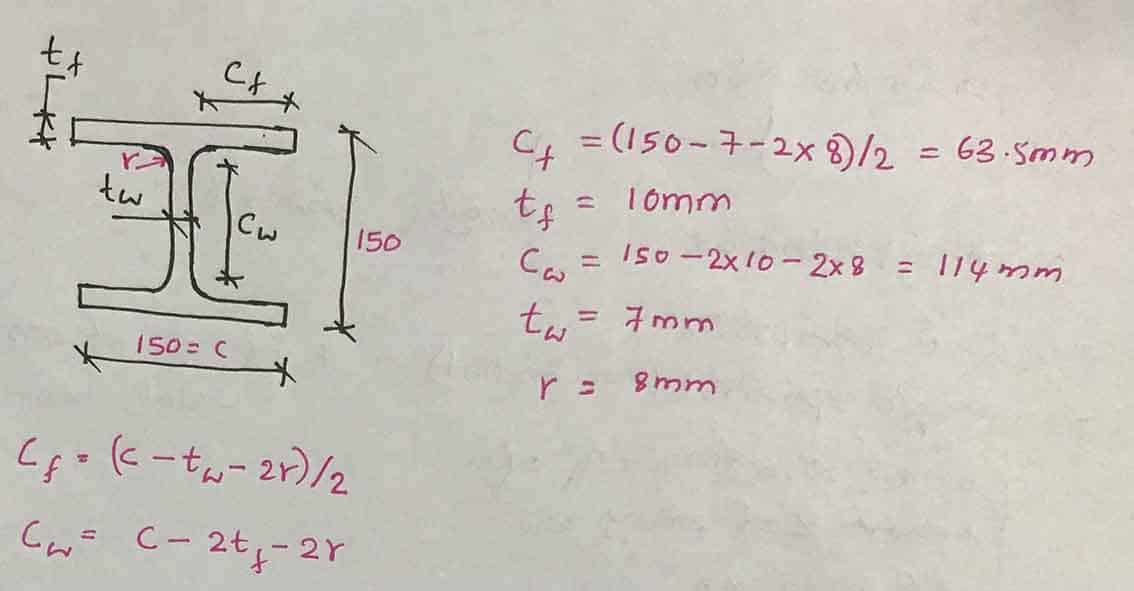
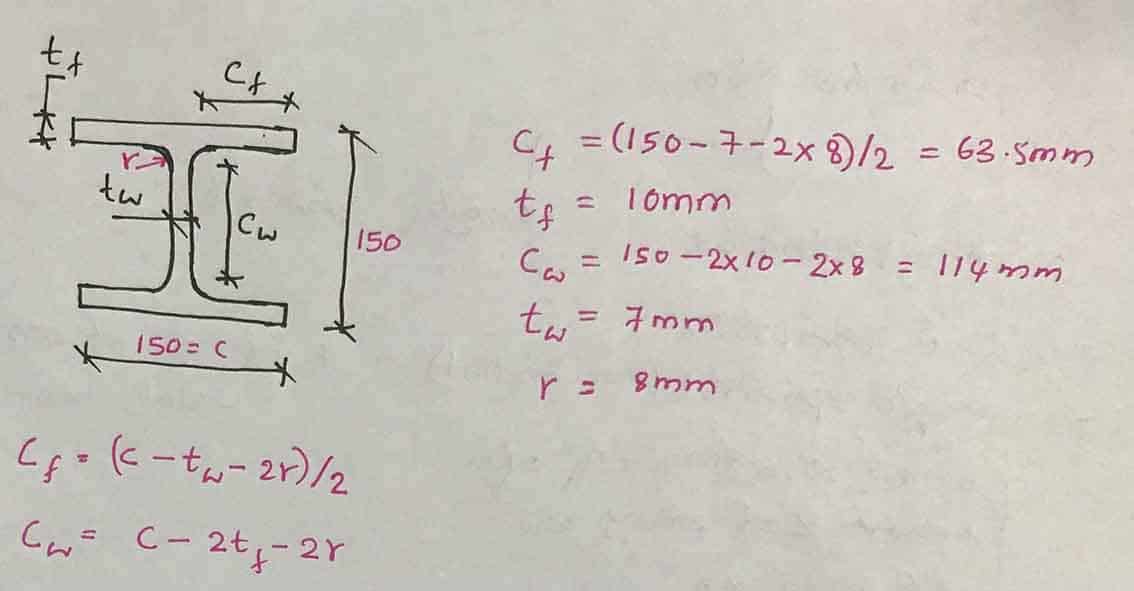
Podemos calcular los límites de delgadez.
mesa
C F /T F = 63,5/10 = 6,35 < 9ε = 9 x 0,92 = 8,82; Sección clase 1
red
C i /T i = 114/7 = 16,3 < 33ε = 33 x 0,92 = 30,36; Sección clase 1
-
Resistencia plástica o resistencia transversal, N c, Carretera
- Perfiles no delgados: Clase 1
N c,Rd = Af j /γ m0 = 3965 x 275/1 = 1.090,4 kN
Después de calcular la resistencia, se debe realizar la siguiente prueba de capacidad.
N Ed. = 500 kN
N Ed./N c,Rd = 500/1090,4 = 0,46 <1
La sección transversal cumple con la resistencia plástica.
- Resistencia al pandeo, N b, Carretera
Primero calcule la resistencia al pandeo según la clase de sección.
Sigamos el procedimiento en el proceso de diseño.
λ1 = 93,9ε = 93,9 x 0,92 = 86,4
Al diseñar el pilar, debemos considerar la resistencia alrededor de cada eje (YY y ZZ).
i = radio de giro
UE JJ = 6,4 cm
UE actualmente = 3,77 cm
M cr = longitud de pandeo
Como los dos extremos de la columna están fijos,
Mcr = 1,0 x L = 3m
λ¯ = Yo cr / Yoλ 1
Eje YY; λ¯ = L cr / Lλ 1 = 3000 / (64 x 86,4) = 0,54
eje ZZ; λ¯ = L cr / Lλ 1 = 3000 / (37,7 x 86,4) = 0,92
Determinemos el factor de imperfección α a partir de la Tabla 6.1 de EN 1993-1-1.
Encuentre la curva de pandeo
h/b = 150/150 = 1 < 1,2
T F = 10 mm < 100 mm
Veamos ahora parte de la tabla 6.2 de EN 1993-1-1,
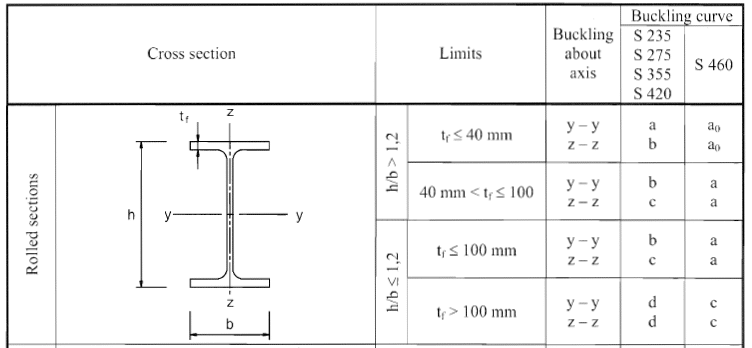
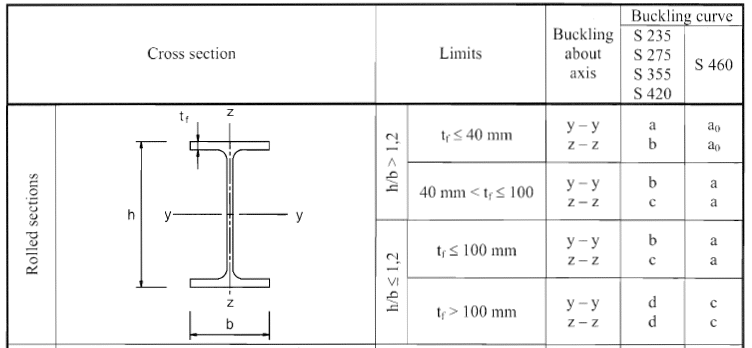
Por lo tanto, la curva jorobada resulta de la siguiente manera
Eje YY-b
Eje ZZ-c
De la Tabla 6.1
| Curva de curvatura | A las 0 | A | B | W. | D |
| Factor de imperfección α | 0,13 | 0,21 | 0,34 | 0,49 | 0,76 |
α en el eje YY = 0,34
α en el eje ZZ = 0,49
Ahora calcula Ø
Ø = 0,5 ( 1 + α( λ¯ – 0,2) + λ¯ 2 )
Sobre el eje YY
Ø = 0,5 (1 + 0,34(0,54 – 0,2) + 0,54 2 ) = 0,7
Sobre el eje ZZ
Ø = 0,5 (1 + 0,49(0,92 – 0,2) + 0,92 2 ) = 1,1
Cálculo del factor de reducción, χ
χ =1 /( Ø + √(Ø 2 –λ¯ 2 )) ≤ 1,0
Sobre el eje YY
χ =1 /( 0,7 + √(0,7 2 – 0,54 2 )) = 0,873 < 1,0
Sobre el eje ZZ
χ =1 /( 1,1 + √(1,1 2 – 0,92 2 )) = 0,587 < 1,0
La χ más baja es el eje crítico contra el pandeo y está disponible una menor resistencia al pandeo.
Por lo tanto,
χ = 0,587
Ahora calcule la resistencia al pandeo N b, Road ,
N b, Camino = χ A f j /γ M1 – No flaco – Clase 1
N b, Carretera = 0,587 x 3965 x 275/1 = 640 kN
- Verificación de capacidad
N Ed. /N b, Carretera ≤ 1,0
N Ed. /N b, Carretera = 500/640 = 0,781 <1
La sección está bien.
Para más información consultar el artículo “Eurocódigo 3: Diseño y construcción de estructuras metálicas” publicado en Wikipedia.

