La viga del puente se construye generalmente como viga pretensada o postensada. Además de las vigas prefabricadas, también se construyen losas de hormigón sobre estribos, alcantarillas tipo cajón, vigas cajón y puentes colgantes, tanto para el tráfico de personas como de vehículos.
El diseño de vigas de puente de hormigón pretensado que se analiza en este artículo cumple con BS 8110 Parte 1.
En este artículo analizamos el diseño ULS (estimación ULS de la capacidad de momento flector) de una viga de puente pretensada con el método de compatibilidad de deformaciones .
Analicemos un poco sobre el método de compatibilidad raíz.


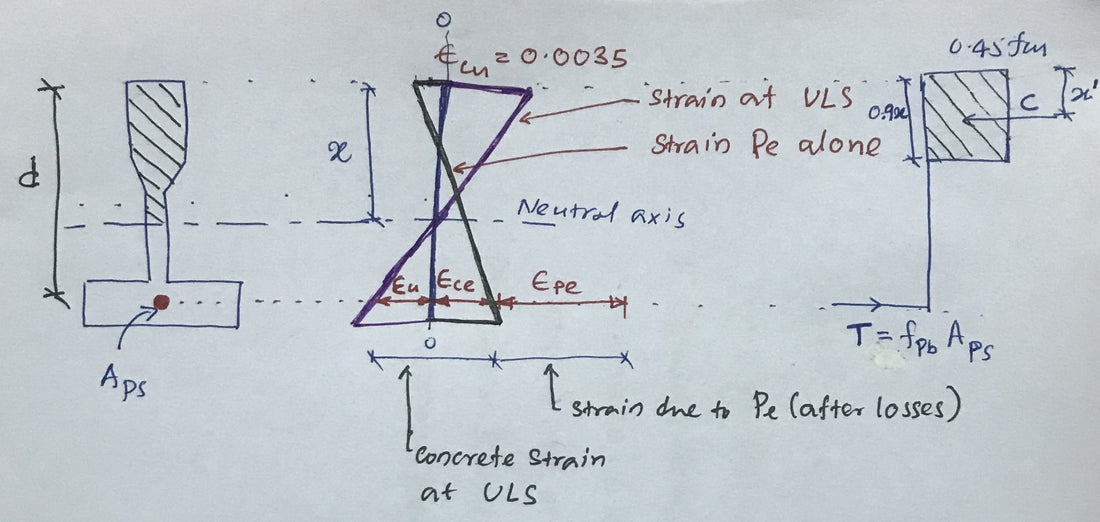
Deformación en estado límite último (ε pb ) Al seleccionar superficies de tensión, preste atención a los siguientes componentes.
- Elongación debida a la fuerza de tracción efectiva (Pe) (después de las pérdidas) – ε Sports
- Deformación causada por la carga aplicada – ε Pai
El alargamiento debido a la precarga Pe se calcula de la siguiente manera
ε Deportes =P t / ( Nota A: .Nota E : )
Donde A nota: es el área de los tendones y E nota: es el módulo de elasticidad del acero.
Durante el pretensado, la compresión es por debajo del eje neutro y la sección está sometida a esfuerzos de compresión ε c y E ε Sports.
Aquí, ε ce es la tensión de compresión en la sección en el plano del acero a través de los “ Deportes ”.
La carga aplicada inicialmente hace que esta expansión ( ε ce ) sea cero y luego se desarrolla la tensión de tracción del acero. El esfuerzo de tracción total desarrollado por la carga en el estado límite último es
ε Padre = ε ce + ε Ela
Avance,
Reducción de la tensión de compresión del hormigón = aumento de la tensión de tracción del acero
Esto se debe a que el acero y el hormigón están en la misma sección. La tensión del hormigón disminuye y al mismo tiempo aumenta la tensión del acero. Ambas cosas suceden al mismo tiempo.
Aquí,
ε ce =f con / E C = (P t /E C ) ( 1/A + e 2 /I)
ε Ela = ε cu (d – x) / x = 0,0035 (d – x) /x
La tensión de tracción del acero se puede expresar como
ε pb = ε Ela + ε ce + ε Deportes
Necesitamos utilizar un proceso iterativo para calcular la profundidad del eje neutro hasta que la fuerza de empuje sea igual a la fuerza de tracción (C = T).
Después de calcular la deformación por tracción (ε pb ), calcule la capacidad de flexión de la sección usando la siguiente ecuación.
M Ela =f pb A nota: (t')
Al calcular la capacidad de flexión de la viga del puente, se realizan los siguientes pasos.
- Suponga una profundidad natural del eje y calcule la fuerza de compresión (C = 0,45 fcu A' C ).
- A continuación, calcule la tensión de tracción en el tendón.
- Para ello se calculan las tensiones de tracción en los tendones ( ε pb = ε Ela + ε ce + ε Sports )
- Y luego encuentras el diamante de imitación de acero en la curva tensión-deformación.
- Compruebe que la fuerza de tracción ( T=f pb A nota: ) y la fuerza de compresión sean las mismas.
- De lo contrario, repita el cálculo cambiando las profundidades del eje neutro hasta que sean iguales.
- Después de determinar el canto del eje neutro, calcular la capacidad de flexión de la sección ( M Ela =f pb A nota: (dd')).
Exploremos esto con un ejemplo práctico.
Datos de diseño de vigas de puente
- Envergadura = 16m
- Peso de la losa = 1 kN/m
- Carga útil = 4 kN/m
- Densidad del hormigón 24 kN/m 3
- Límite elástico a tracción, f pu = 1670 N/mm 2
- Área del tendón, nota A: = 882 mm 2
- Resistencia del cubo de hormigón, f cu = 40 N/mm 2
- Área de sección transversal, A = 121.000 mm 2
- Módulo de elasticidad del acero, E nota: = 205kN/mm 2
- Módulo de elasticidad del hormigón, E cu = 28 N/mm 2
- Momento de inercia del área de la sección transversal, I = 5.236×10 9 mm 4
- Fuerza de precarga, P t = 744 kN


Calcular el par nominal
Los factores de carga de diseño se adoptaron de BS 8110.
Área de sección = 121.000 mm 2
Peso propio de la viga = 121.000 x 10 -6 x 24 = 2,9 kN/m
Carga de diseño = 1,4 (2,9 + 1) + 1,6 x 4 = 11,86 kN/m
Par nominal = wl 2 /8 = 11,86 x 16 2 / 8 = 379,52 kN·m
Prueba de resistencia al momento
Calcular la profundidad del eje neutro.
Suponga que el eje neutro, x = 400 mm desde la fibra exterior más superior
Altura del bloque de tensión de compresión = 0,9 x = 0,9 x 400 = 360 mm


Área del bloque de tensión de compresión, A' C = ON 1 + UM 2 + UM 3
A' C = 150×200 + 0.5x(200+100)x75 + 135×100 = 54.75×10 3 milímetros 2
Fuerza compresiva
C = 0,45 fcu.A' C
C = 0,45 x 40 x 54,75 x 10 3 = 985,5 × 10 3 N = 985,5 kN
Calcular la fuerza de tracción
T=f pb Una nota:
Primero tenemos que calcular la tensión de tracción (f pb ). Usaremos voltaje en esta sección.
ε pb = ε Deportes + ε ce + ε Ela = P t /(A obs: .E obs: ) + (P t /E C )(1/A + t 2 /EU) + 0,0035(dx)/ x
ε Deportes =P t /( Nota A: .Nota E : ) = 744×10 3 / (882×205×10 3 ) = 4,11 x 10 -3
ε ce = (P t /E C )(1/A + t 2 /l = ( 744×10 3 /28×10 3 ) ( 1/121000 + 199 2 /5.236×10 9 ) = 0.42 x 10 -3
ε Ela = 0,0035(dx)/x = 0,0035x ( (199+364) -400 ) / 400 = 1,43 x 10 -3
ε pb = 4,11 x 10 -3 +0,42×10 -3 + 1,43×10 -3 = 5,96×10 -3
El alargamiento del tendón es 5,96 x 10 -3 ≈ 0,006
A partir del diagrama de tensión y deformación para cables en BS 8110 Parte 01, se puede tener en cuenta la siguiente información para el diseño


La siguiente información está disponible.
- ϒ M = 1,5
- Fpu = 1670 N/ mm2
- Y tenga en cuenta: = 205 kN/mm 2
F pu /γ M = 1670 / 1,15 = 1452,2 N/mm 2
0,8f pu /γ M = 1452,2 x 0,8 = 1161,7 N/ mm2
F pu /γ ME nota: = 1670 / (1,15 x 205×10 3 ) = 0,0071
0.8f pu /γ M E nota: = 0.0071 x 0.8 = 0.0057
Ahora los valores en la imagen de arriba se pueden marcar de la siguiente manera.


Mediante interpolación lineal podemos determinar la tensión en los tendones.
Fpb = 1175,3 N/ mm2
área del tendón, nota A: = 882 mm 2
Ahora podemos calcular la fuerza de tracción,
T=f pb A nota: = 1175,3 x 882 = 1036,6×10 3 N = 1.036,6 kN
C = 985,5 kN
T ≠ C, la profundidad del eje neutro supuesta es incorrecta. Tenemos que repetir el mismo procedimiento hasta que T = C.
Es posible que necesitemos realizar varias iteraciones para acercarnos a la profundidad correcta del eje neutro.
Primero comprobamos el rango de profundidad del eje neutro.
Podemos asumir C = 1036,6 kN (fuerza de tracción) y luego verificar la profundidad
C = 0,45 fcu.A' C
1036,6×10 3 = 0,45x40x A'C
A'C = 57588,9 mm2
57588,9 = 150×200 + 0,5x(200+100)x75 + (0,9x – 150 – 75 )x100
x = 431,54 milímetros
Por tanto podemos decir que “x” debe ser menor que este valor.
Supongamos que x = 425 mm
ε pb = 4,11 x 10 -3 +0,42×10 -3 + 0,0035x ( (199+364) -425 ) / 425 = 0,0057
Siga el mismo procedimiento que en la tabla anterior.
Fpb = 1161,7 N/ mm2
T =f pb A nota: = 1161,7 x 882 = 1024,6×10 3 N = 1.024,6 kN
C = 0,45.fcu.A' C = 0,45 x 40 x (150×200 + 0,5x(200+100)x75 + 157,5×100} = 1026×10 3 N = 1.026 kN
Por lo tanto podemos concluir que T ≈ C
Entonces, para calcular la capacidad de flexión, considere x = 425 mm.
M Ela =f pb A nota: (t')
Donde d' es el centro de gravedad del bloque de tensión de compresión.


d' se puede calcular calculando el momento alrededor de un borde. Entonces el cálculo no se toma en consideración porque es un cálculo simple.
d' = 159,6 mm
Calculemos la capacidad de flexión.
M Ela =f pb A nota: (t')
Esta ecuación se puede escribir de la siguiente manera:
M Ela = T (d – d')
M Ella = 1024,6 (563 -159,6)/1000 = 413,3 kN·m
La capacidad de flexión es de 413,3 kNm y el momento flector aplicado es de 379,52 kNm. La sección es apta para doblarse.
Sin embargo, la sección debe someterse a prueba de corte. La información sobre el tamaño de las vigas de hormigón pretensado se puede encontrar en un artículo aparte.
Se puede consultar el artículo Construcción de puentes según BS 5400 para proporcionar más información sobre la teoría del diseño de vigas de puentes.
Lectura adicional sobre piezas prefabricadas de hormigón: se podría enviar un artículo de Wikipedia sobre hormigón pretensado .