Statement of Thevenin's theorem
Any permutation of linear bilateral circuit elements and active sources, plus connections or complications connected to a specific load R M possibly replaced by a simple two-terminal network consisting of a single voltage source of V M volts and a single resistor R equation in series with the voltage source, across the two terminals of the resistive load R M. VTH is the open circuit voltage, measured at the two relevant connections, with load resistance R M removed. This voltage is known as Thevenin equivalent voltage. OR equation is the equivalent resistance of the given network seen across the terminals, where R M is connected, but with R M removed, all active sources are replaced by their internal resistances.
Explanation of Thevenin's Theorem
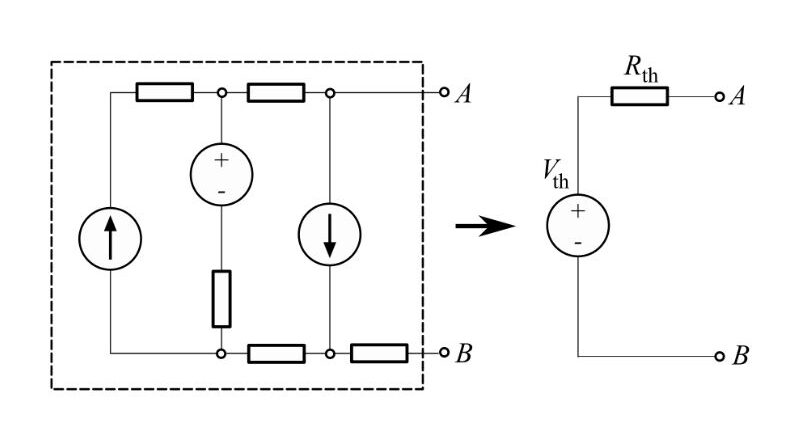
The Thévenin equivalent theory about the terminals of interest can be explained by considering the circuit shown in Fig. The AB connections are the connections of interest through which R M connected. Then the Thévenin equivalent can be obtained through the load terminals AB, as shown in Fig.
Superposition theorem
The voltage Vº is obtained through connections AB with R M removed. Hence Vº is also called open circuit Thévenin voltage. The circuit for calculating Vº is shown in Fig. a for the network considered above. At the same time, R. equation is the equivalent resistance considered across terminals AB with R M removed, the voltage sources replaced by short circuits and the current sources replaced by an open circuit. This is shown in Fig – b.
When obtaining V º Any network simplification technique can be used. If the circuit is replaced by the Thévenin equivalent in the load resistance, the load current is obtained as
I M =V º /(R M +R equation ).
Using this theorem, the current through each branch of the circuit can be found by treating the branch resistance as a load resistance and finding the Thevenin equivalent at the two terminals of that branch resistor as the load resistance and finding the Thevenin equivalent at the two branch terminals.
Steps to apply Thevenin's theorem
-
Remove the branch resistor through which the current will be calculated.
-
Calculate the voltage at these open terminals using any network simplification technique. This is V.º.
-
Calculate R equation seen through the two terminals of the branch from which the current is calculated, removing the resistance of this branch and replacing all independent sources with their internal resistances. If internal resistances are unknown, replace independent voltage sources with short circuits and independent current sources with open circuits.
-
Draw the Thevenin equivalent with source V º with resistance R equation in series, through the connections of a relevant branch.
-
Reconnect the branch resistor. Let it be R. M The current required through the branch is given by
I = V º / (R equation +R M )
Limitations of Thevenin's Theorem
The limitations of Thevenin's theorem are:
-
It does not apply to circuits made up of non-linear elements.
-
Does not apply to one-way networks.
-
There must be no magnetic coupling between the load and the circuit, which must be replaced by Thévenin's theorem.
-
Sources controlled on the load side must not be controlled from any other part of the circuit.