Material length
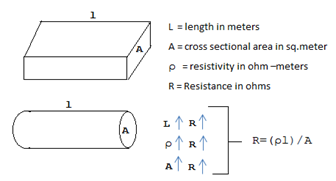
The resistance of a material is directly influenced by its length. This is one of the basic principles of electrical engineering, the so-called “resistance-length relationship”. This relationship is an important aspect of Ohm's law, which describes how current, voltage, and resistance are related in a circuit.
The resistance-length relationship can be explained using the following points:
Direct proportionality
The resistance of a conductor is directly proportional to its length. This means that as the length of a conductor increases, its resistance factor also increases, assuming all other factors remain constant. Conversely, as the size of the conductor is reduced, the resistance decreases.
Electron flow
When an electric current flows through a conductor, electrons are associated with it. As they move, these electrons collide with atoms in the material. In a longer conductor, electrons have to travel a greater distance and therefore suffer more collisions, increasing the overall resistance to their movement and resulting in higher resistance.
resistance and length
The resistance of a material is also influenced by its resistivity (ρ), an intrinsic property of the material. The resistance of a conductor can be calculated using the formula R = ρ * (L / A), where R is the resistance, ρ is the resistivity, L is the length, and A is the cross-sectional area. This formula illustrates the direct relationship between strength and size.
Units and measurements
The SI unit of resistance factors is ohm (Ω). Suppose the length of a conductor is measured in meters (m) and the cross-sectional area is measured in square meters (m²). In this case, the resistance can be determined directly using the above formula.
Forms
Understanding the relationship between strength and length is crucial for many practical applications. For example, when designing electrical circuits, engineers consider the length of wires and conductors to ensure that resistance remains within acceptable limits. In high power applications, minimizing conductor size helps reduce power losses due to heat generated by resistance.
voltage drop
A longer conductor can result in a greater voltage drop when current flows. This voltage drop can affect the performance of electrical devices and require compensation or adjustments to the circuit design.
Electric charge and current

Electric current is the flow of electrical charge through a conductor and plays a fundamental role in the world of electricity and electronics. Charge, the set of properties of matter responsible for electrical interactions, can be positive (protons) or negative (electrons). When a charge is in motion, it represents an electric current. This movement can be compared to the flow of water in a river, with the water molecules representing the charges.
loading
Charge is a fundamental property of matter and can be positive or negative. In an atom, protons carry a positive charge, electrons have a negative charge, and neutrons are neutral. Charges exert electromagnetic forces on each other; they attract each other (opposite charges) or repel each other (same charges).
Electric current
Electric current is the flow of electrical charge through a conductor. It is measured in amps (A) and represents the speed at which electricity moves. Electricity can flow in two ways: direct current (DC), in which charges continually flow in one direction, and alternating current (AC), in which charges regularly reverse the direction of flow.
Resistance
Resistance is the resistance experienced by electrical charges as they pass through a conductor. It is measured in ohms (Ω). Resistance prevents current flow and converts some of the kinetic energy into heat. Conductors with low resistance allow current to flow more easily, while materials with high resistance impede flow.
Ohm's Law
Ohm's law, named after the German physicist Georg Simon Ohm, connects these three concepts: electric current (I), voltage (V) and resistance (R). This is expressed mathematically as V = I * R, where V is the voltage, I is the current and R is the resistance. This equation shows that the voltage across a conductor is directly proportional to the current flowing through it and the resistance it offers.
Relationship between current and resistance
According to Ohm's law, the current flowing through a conductor is directly proportional to the applied voltage and inversely proportional to its resistance. This means that increasing voltage results in higher current, while increasing resistance for a given voltage reduces windage.
Effects
- Heat generation : Resistance causes energy to be converted into heat when current flows through a conductor. This effect is used in heating elements such as toasters and electric stoves.
- voltage drop : A voltage drop occurs between components with resistance in a circuit. This can affect the performance of devices as the available voltage decreases.
- Power failure : Resistance leads to loss of power in electrical systems. The higher the resistance, the more energy is lost as heat, which can be a problem in high power applications.
- Circuit design : When designing circuits, engineers must ensure that components receive the current and voltage necessary for proper operation.
temperature
The temperature of the material influences the resistance value. Typically, the material gets hotter as the temperature increases. The effects of small temperature fluctuations on resistance are not considered negligible.Electric potential and potential difference

Electrical potential, often called “potential,” is a scalar quantity that describes the electrical potential energy per unit charge at a point in space due to the presence of an electric field. It represents the work required to move a positive charge from infinity to a specific point within the electric field.
Mathematically, the electrical potential (V) at a point is given by the following equation:
Where,
- What is the electrical potential at the moment?
- electrical potential energy associated with point charge?
- is the size of the test load.
The SI unit of electrical potential is the volt (V).
Potential difference (voltage)
Potential difference, often referred to as “voltage,” is the difference in electrical potential between two points in an electric field. It quantifies the work done per unit load by moving a head between these two points.
Mathematically speaking, the potential difference ( ABSENT between point A and point B is given by:
AB =
Where,
- ABSENT the potential difference between points A and B.
- the electric potential at point B.
- the electric potential at point A.
The SI unit of potential difference is also volt (V).
Important points
- Electric potential is a property of a point in space and describes how much electrical potential energy a unit of positive charge would have at that point.
- The potential difference (voltage) between two points is the work done per unit charge when a head is moved between those points. It is a measure of the difference in energy per unit charge.
- Voltage is the driving force that moves charges through a circuit. It is responsible for the flow of electrical current.
- In a uniform electric field, the potential difference between two points is directly proportional to the distance between those points.
- Positive charges move from a higher potential to a lower potential (lower voltage) to reduce their potential energy, while negative charges move in the opposite direction.
- The concept of potential difference is crucial to understanding circuits, distribution of electrical energy, and various electrical devices.
- In a circuit, voltage sources (such as batteries) create potential differences that control the flow of current through components.
Temperature Effects
- Temperature coefficient
- Atomic vibrations
- Thermistors
Temperature coefficient
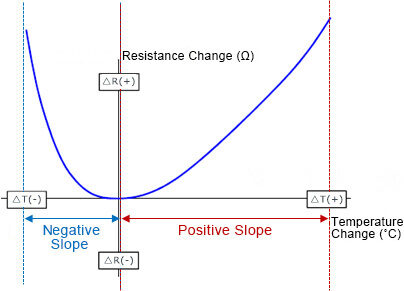
Different materials respond differently to temperature changes, resulting in positive or negative TCR values. A positive TCR means that resistance increases with temperature, while a negative TCR means that resistance decreases with increasing temperature. This distinction has significant implications for practical applications. Explain how TCR is calculated using the formula TCR = (Rt – R0) / (R0 × ΔT), where Rt is the resistance at temperature t, R0 is the reference temperature, and ΔT is the temperature difference between t and reference temperature . Provide examples of typical TCR values for common materials such as copper (approximately +0.0039 Ω/°C) and silicon (approximately -0.075 Ω/°C).
Atomic vibrations
The atoms of a material are not static; They are in a constant state of motion due to their thermal energy. Atomic vibrations occur when particles oscillate around their equilibrium positions. These oscillations can be classified as longitudinal (parallel to the direction of wave propagation) or transverse (perpendicular to the direction of wave propagation). Atomic vibrations have different effects on conductors and insulators. In conductors, the movement of charge carriers (electrons) is already relatively free, and atomic vibrations mainly cause scattering events. This dispersion increases resistance in conductors as the temperature increases. In insulators, where electrons are tightly bound to atoms, atomic vibrations affect electron mobility, leading to changes in resistivity.
Thermistors
Thermistors are typically made of semiconductor materials, such as metal oxides or polymers, with a negative temperature coefficient of resistance (NTC) or a positive temperature coefficient of resistance (PTC). NTC thermistors show a decrease in resistance as the temperature increases, while PTC thermistors show an increase in resistance as the temperature increases. The temperature dependence in thermistors results from changes in the concentration of charge carriers (electrons or holes) with changes in temperature. With NTC thermistors, as the temperature increases, more charge carriers become available for conduction, which leads to a drop in resistance. PTC thermistors work on the principle of materials with a positive temperature coefficient, where resistance increases due to the decrease in the concentration of charge carriers with temperature.
Conclusion
By understanding these factors, we can manipulate and optimize strength in our designs. Whether selecting the most appropriate materials for specific applications, considering the effects of temperature on circuit performance, or designing precise contact points to minimize resistance, our knowledge allows us to design more efficient and reliable systems.