The worked steel beam design example explains the construction of a simply supported beam with a uniformly distributed load. The beam is considered simply supported and the design data for calculating the bending moment and shear forces are provided below.
Furthermore, the cross-sectional properties to be considered are specified in the individual test steps.
Theoretical aspects and code design procedures are discussed in the article Design Steel Beams Conforming to BS 5950 .
Design data
- UDL load 20 kN/m
- Beam extension 6m
- The beam is simply supported
- Design strength of steel, Py = 275 N/mm 2
Maximum bending moment
= wl 2 /8 = 20 x 6 2 / 8 = 90 kN m
Maximum shear force
= wl/2 = 20 x 6/2 = 60 kN
Consider universal conveyor 500x200x89.7 kg/m (P j = 275 N/mm 2 )
Section data
- T = 500mm
- T = 16mm
- t = 10mm
- B = 200mm
- b = 100mm
- R 1 = 20 mm
- d = 500 – 16 x 2 – 2 x 20 = 428 mm
- S X = 2175 × 10 3 mm 3
- Z X = 1914 × 10 3 mm 3
- R j = 43.3 mm
Let's start calculating the steel beam design. As part of this steel beam design calculation, the following tests are carried out.
- Section classification
- Shear design
- Bending construction
- Check for torsional buckling
- Deflection control
- Bridge Bearing Test
- Web buckling test
Section classification
The first step in designing a steel beam is to classify the cross section to determine whether it is plastic, semiplastic, compact, or slender.
T = 16 mm, P j = 275 N/mm 2
ε = (275/P j ) 0.5 = 1
Check the flange
b/T = 100/16 = 6.25 < 9ε = 9 – Flange is made of plastic
Check the web
d/t = 428/10 = 42.8 < 80ε = 80 – The net is made of plastic
Furthermore, d/t < 70ε = 70 - therefore no shear buckling check is required
Therefore, the section is plastic
Design for shear forces
Design shear force, F contra = 60kN
P contra = 0.6p j A contra = 0.6p j tD = 0.6 x 275 x 10 x 500 x 10 -3 = 825kN
F against
against Shear capacity is OK
Depending on the shear force, the construction of the steel beam decides whether the cross section will be exposed to a low or high shear force.
Flexible construction
Check whether the section is subject to low or high shear
60% xp against = 0.6 x 825 = 495kN
F vs <0.6P vs Low Shear Section
M C must be less than 1.2P j Z X or P j S X in accordance with Section 4.2.5.1 and Section 4.2.5.2
M C ≤1.2P j Z X = 1.2x275x1914x10 3 x 10 -6 = 613.62 kN m
M C = P j S
Therefore,
MC = 598.125 kNm > 90 kNm
Folding well
Detect flexural and torsional buckling
M X < M b /M LT
No intermediate constraints were considered in this example
M LT = 0.925, Table 18, BS 5950
M b =P b S X Section 4.3.6.4
There are two methods for checking lateral torsional buckling, as described in the article Construction of steel beams to BS 5950 . These are the strict method and the simplified method.
In this steel beam design example, we discuss both methods to further explain the procedures that need to be followed in both methods.
Further and beyond The main difference between these two methods is the assessment of flexural strength .
Rigorous method
Mb = PbSX
P b depends on λ LT and P j
λ LT =uvλ√(β i )
λ = I E /R j
M E – taken from Table 13 in accordance with Section 4.3.5.1 and taking into account L LT = L – span
M E = 1.0L LT = 1 x 6 = 6 meters
λ = I E /R j = 6,000/43.3 = 138.568
Section 4.3.6.8 applies to laminated profiles I and H
x = D / T used with u = 0.9
x = D / T = 500/10 = 50
β i can be found in section 4.3.6.9
β i = 1 for class 1 plastic profiles or class 2 compact profiles
v – slenderness factor, which is determined in Table 19 based on λ / x and η
λ/x = 138.568/50 = 2.771
η = 0.5 for isosceles flanges
v = 0.919 from Table 19
λ LT =uvλ√(β i ) = 0.9 x 0.919 x 138.568 x √(1) = 114.6
λ ELA can be found in Table 16 (see table below)
If λ ELA ≥λ LT ; P b =P j or else P b can be found in Table 16 for rolled profiles.
If λ ELA ≥λ LT It is not necessary to take torsional buckling into account; otherwise, a torsional buckling check must be carried out.
P j = 275 N/mm 2 ; λ ELA = 37.3
λ ELA <λ LT Therefore, check for torsional buckling
From Table 16 for λ LT = 114.6; P b = 102 N/mm 2
M b =P b S X = 102 x 2175 x 10 3 x 10 -6 = 221.85 kN m
M b /M LT = 221.85 / 0.925 = 239.838 kNm
Therefore, MX = 90kNm
section is sufficient .
Simplified method
Note: It is not necessary to use both methods when sizing a beam. Just follow the simplified or strict method.
M b =P b S X : Paragraph 4.3.7
With this method, the determination of P b is different from the previous method. This method provides conservative answers. P b can be found in Table 20 of BS 5950 based on √(β i ) (I E /R j ) and D/T
β i = 1; previous calculation
M E /R j = 138.568; previous calculation
√(β i ) (I E /R j ) = 1 0.5 x 135.568 = 138.568
D/T = 500/16 = 31.25
P b = 116.646 N/mm 2 From table 20
M b = P b S
M b /M LT = 253.705 / 0.925 = 274.3 kNm
Therefore, MX = 90kNm
section is enough
Detour
The maximum deflection (δ) for a simply supported beam with uniform distribution can be calculated using the following equation.
δ = 5W t M 4 / (384EI)
This equation can be further simplified as follows.
δ = 0.104 M Max M 2 / (EI)
As we evaluate deflection based on applied loads, we assume an applied load of 10 kN/m for this calculation.
δ = 0.104 x 90 x 10 6 6,000 2 / (205×10 3 x 478 x 10 6 ) = 1.7mm
Assuming brittle surfaces are used
Wingspan / 360 = 6000/360 = 16.7 mm
δ < span / 360, so the deflection is ok
Different methods for calculating distractions are explained in the Wikipedia article distraction (technology) .
Web load capacity
When designing steel beams, the load capacity of the web must be checked. In this category, the load capacity of the web and buckling are tested.
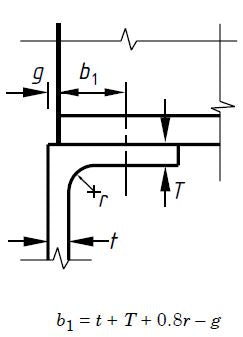
P head = (b 1 + nk) tP Yes
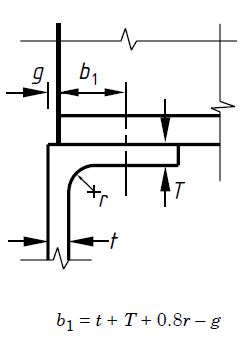
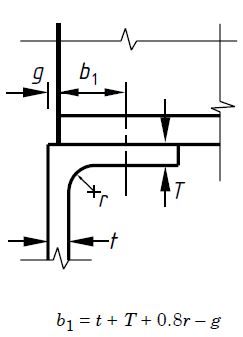
t = 10mm
T = 10mm
r = 10mm
g = 5mm
bt = 5mm
b 1 = t + T + 0.8r – g = 10 + 10 + 0.8 x 10 – 5 = 23 mm
k = T + r = 16 + 20 = 36 mm (for laminated profile)
at the end,
n = (2 + 0.6b t /k) but ≤ 5
n = (2 + 0.6 x 5/36) = 2.083 < 5 P Yes = 275 N/mm 2 from Table 9
P head = (b 1 + nk) tP Sim = (23 +2.083 x 36) x 10 x 275 x 10 -3 = 269.5kN
The load capacity is 60 kN.
The bridge bearing is ok and no reinforcements are needed.
If F X >P head we have to provide reinforcements to reduce the compensating forces (F X -P head ). The load capacity of the reinforcements is given by P S = ON s.net P j . Where a s.net is the stiffness cross-sectional area. If the web and stiffness have different strengths, the smaller value should be used to calculate both P. S and P face .
Bridge buckling
When a t ≥ 0.7 days
P X = 25εt P heads /√( ( b 1 + nk) d)
When a t <0.7 days
P
Where
At t = 0.7d = 23/2 = 11.5 mm <0.7 x 428 = 300 mm
P
P
FX
X
No reinforcements are needed.
The bar meets all tests.