Check deflection of panels in accordance with BS 8110 Part 1
The method for checking slab deflection is similar to checking beam deflection. Checking slab deflection is included in the beam design section of BS 8110 Part 01.
Deflection can be checked using two methods. If you know the maximum deflection for the corresponding load case, you can check whether it is within limits. The code specifies maximum deflection limits based on spans.
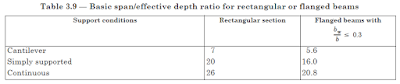
Another method of controlling deflection is to limit the relationship between base span and effective depth to certain values given in Table 3.9 of BS 8110, Part 01, 1997.
The following table lists the basic span/depth relationships for rectangular sections and flange sections.
Depending on the type of slab boundary condition, the span/depth ratio is selected from the table above. For example, if the slab is simply supported, we choose 20 as the basic relationship between span and depth.
The values indicated in the table above can be changed by multiplying the tensile reinforcement, the compression reinforcement and the creep and shrinkage deformation factors. Typically, creep and shrinkage factors are not applied.
The modification factor for tensile reinforcement can be found in Table 3.10 of BS 8110 Part 01.
Look the following picture.
If we know the operating stress and bending stress, we can find the modification factor directly from the above table or use the equations in the following table to calculate the modification factor.
The modification factor for compression reinforcement can be found in Table 3.11 of BS 8110 Part 01 1997.
If we provide compression reinforcement, it can be multiplied by this factor. Otherwise, the factor will be considered 01 if we do not provide compression reinforcement.
Example
Data
Useful depth = 120 mm
Reinforcement requirement = 197 mm 2
Reinforcement provided = 393 mm 2
Wingspan = 3000 mm
Bending moment = 4.8 kNm
Steel strength = 460 N/mm 2
No compression reinforcement is provided
For this example, consider a plate simply supported
Allowed extension/depth = 20
Determination of Modification Factor for Tensile Reinforcement
As we know the characteristic strength of the steel and the cross-section of the required and existing reinforcement, we can calculate the design working stress (fs) for the equation in Table 3.10.
fs = 2x460x197 / (3×393)
= 153.7 N/mm 2
The equation modification factor is given in Table 3.10.
Modification factor = (0.55 + (477 – 153.7) / {120(0.9 + 0.33)) ≤ 2
= 2.19 > 2
Therefore, the modification factor is 2.
Allowed span/depth ratio = 20 x 2 = 40
Actual span/depth ratio = 3000/120 = 25
The permitted span-to-depth ratio is greater than the actual span-to-depth ratio.
So distraction is okay.