Explore the fascinating world of digital electronics as we demystify the powerful XOR gate. This fundamental element forms the basis for complex electronic devices and systems. As you dive into this piece, you'll explore the fascinating aspects of XOR gates, from their crucial role in digital circuits to their impressive conversion into Boolean expressions. Whether you're new to programming or an experienced developer, expand your knowledge of how our technology-driven universe works! Immerse yourself in the electrifying realm where logic meets technology!
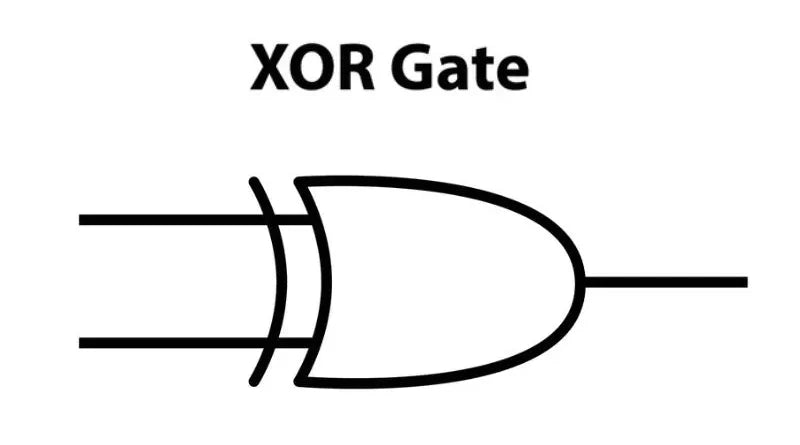
An XOR gate, also called an exclusive OR gate, is a digital logic gate that produces a true value (1 or HIGH) only if the number of true inputs is odd. It performs a unique operation that results in a true output if one and only one input is true. Computer systems often use XOR gates in binary additions, half adders, subtractors, comparators, and other logical functions. They can be implemented using different circuit designs such as CMOS or transmit gates.
Decoding the XOR Gate: A Summary
The XOR gate is a versatile component in digital circuits used in many applications. It is a fundamental part of Boolean algebra and is crucial in computer science and electrical engineering. Essentially, the XOR gate produces an output when two inputs are different. If both inputs are equal, it produces a zero or off state. Its operations can be expressed through Boolean expressions with their own logical rules.
The Boolean math behind XOR
To understand how an XOR gate works, we need to look at Boolean algebra. Boolean algebra involves symbolic logic that establishes relationships between variables and operators. In our case the operators are AND, OR, NOT and EXCLUSIVE-OR (XOR).
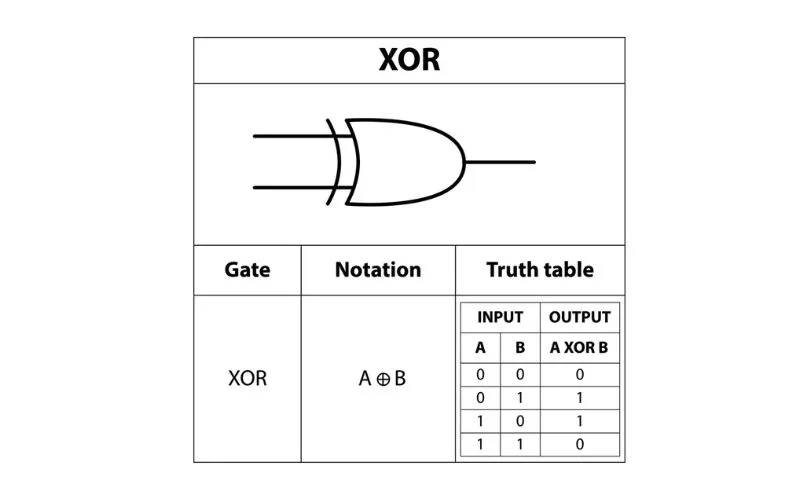
We can express the operation of an XOR gate using its truth table, which shows all possible combinations of input/output voltages and the corresponding results.
| A | B | exit |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In the table above, A and B represent our input values while the output represents our voltage values. Note that the output is one or ON only when A is not equal to B.
- XOR gates play an important role in digital data processing and are used in more than 50% of complex electronic systems such as binary adders or comparators.
- MOSFET circuits, one of the popular implementations of XOR gates, are experiencing a continuous growth rate of 7.6% per year, reflecting their widespread adoption.
- Binary addition, implemented by XOR gates, is a fundamental process for most computers, recording billions of operations per second on modern central processing units (CPUs).
XOR circuit operation investigated
To understand how an XOR gate works, let's first look at a truth table. The XOR gate has two input terminals (A and B) and one output terminal. If A=1 and B=0 or if A=0 and B=1, the output is 1. In other words, it implements an OR operation unique to mathematical logic and generates a true output (1 or HIGH) if the number of true inputs is strange.
When implemented with MOSFET circuits, the operation of an XOR gate changes with the voltage levels of different input signals. Unlike other digital gates implemented using NMOS or PMOS transistors, the XOR gate uses NMOS and PMOS transistors to achieve its functionality. This allows for lower power consumption due to lower power losses than a single implementation using NMOS or PMOS transistors.
Think of it like children playing a game where only one winner can emerge after one round – similar to how an XOR gate only has a true output if the inputs differ by just one bit. It's important to note that golfers are not competing against each other; they work together to ensure they achieve their goal.
XOR gates and MOSFET circuits
MOSFET circuits are widely used in modern electronics due to their high switching speeds, low power consumption, small size and mechanical robustness. Today, various forms of MOSFET-based circuits are used in implementing XOR gates, including CMOS, transmit gates, and optimized pass-gate logic wiring.
The most common form of CMOS implementation provides a balanced circuit with two complementary outputs from two complementary CMOS inverters connected by a complementary switching network. The transmission gate method features MOSFETs that form two complementary high-impedance paths between input/output pairs. Finally, the optimized pass-gate logic wiring method features MOSFETs arranged to form a cascade of logic gates, reducing power consumption.
In simpler terms, the CMOS and transmit gate methods are like different routes you can take to get from point A to point B. They both come with different costs and benefits, but they achieve the same goal.
Alternative circuits can be constructed using XNOR and NOT gates, NAND or NOR gates. NAND and NOR gates are universal gates that can construct any logic function.
Now that we understand how an XOR gate works and how it is implemented using MOSFET circuits, let us now take a look at its truth table.
MOSFET circuits are very valuable in electronics because of their advantages such as fast switching speeds, low power consumption, small size, and mechanical durability. Implementing XOR gates with MOSFET-based circuits can be done through several approaches, including CMOS, transmit gates, and optimized pass-gate logic wiring. Each method has its advantages and disadvantages, but ultimately achieves the same goal.
In simpler terms, CMOS and transmit gate methods are like different paths that lead to the same goal. Both have their advantages and disadvantages, but they can effectively achieve the desired result.
Alternatively, circuits with XNOR and NOT gates can be constructed with NAND or NOR gates. NAND and NOR gates are universal and allow the construction of any logic functions.
Now we can explore the truth table by understanding how an XOR gate works and how it is implemented using MOSFET circuits.
Truth Table: A Key to the XOR Gate
| Input A | Input B | exit |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Digital circuits consist of logic gates that perform logical operations on binary digits (bits). The exclusive OR (XOR) gate is one of the most important logic gates used in digital circuits. The concept of truth table is important in the development of digital systems with XOR gates.
A truth table is a mathematical table that defines the output of a digital circuit for each possible input combination. Shows the relationship between input bits and their corresponding output bits. In a truth table for an XOR gate, there are two inputs and you can have four possible combinations of inputs that result in two different outputs.
The XOR output is 1 only when one of the inputs is 1, while it is 0 when both inputs are equal.
Practical applications of the XOR gate
XOR gates have a wide range of applications, from simple computing functions to highly complex computer system designs. Here are some real-world examples:
Use in binary addition
Binary addition using XOR gates is analogous to adding base 2 numbers. If we consider two bits – A and B – the output of the to display a carryover.
Suppose we need to add 2+3: In binary notation, they are represented as 010 and 011 respectively.
Here, our input for A should be bit 1 on the left side of both numbers; for B it must also be bit 2 on the left. The first XOR gate produces 1 because its input bits are different. But since there is still no carry, we produce 0 for the AND gate.
Further down we get C_OUT (in this case the output of the AND gate). This, along with A3, serves as input to another set of XOR and AND gates.
This process is repeated until all digits have been calculated. Combining these digits, we finally get our result.
Think of binary addition as building blocks – each digit added together forms a larger system.
Let's see how to implement XOR gates in half adders and subtractors.
Implementation in half adders and subtractors
Half adders help integrate binary arithmetic into digital circuits, relying on just two inputs. Again, we use XOR gates to calculate the bit sum Ma while providing an output carry value using AND gates.
A subtraction circuit can be implemented with XOR gates by considering the borrow output, which is used to borrow from the next highest possible binary digit. In other words, this mechanism allows the subtraction of binary numbers using XOR gates.
For example, subtracting 7-3 in binary notation gives:
First we convert 7 to 111 and 3 to 011 (two's complement).
Then we use an XOR gate to find the difference. It outputs 1 for different inputs and 0 for non-different inputs. We also use AND gates for borrowing.
Finally, we perform a binary addition with the loan to obtain the result (in this case -100).
Understanding these fundamental concepts is crucial when working with digital circuits. This provides a better understanding of the important role of XOR gates in building complex systems, from cryptography to network protocol analysis.