Note: It is recommended to follow this series of VHDL tutorials in order, starting with the first tutorial .
In the previous tutorial, VHDL Tutorial – 19 we designed a 4-bit binary counter using VHDL.
In this tutorial, we will:
- Write a VHDL program to construct a 4-bit binary to gray and gray to binary code converter
- Check the program output waveform (digital circuit) with the code converter truth table
The 4-bit binary to gray code converter
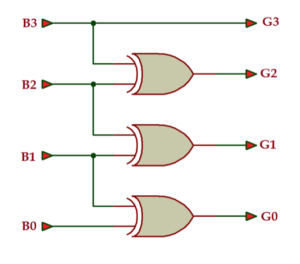
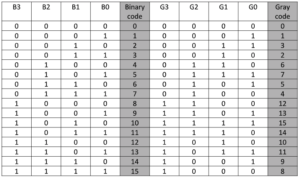
Truth table
Now let's write, compile and simulate a VHDL program. Then we will get the waveform output and check it with the given truth table.
Before you begin, be sure to review the step-by-step procedure provided in VHDL Tutorial – 3 for designing the project. This will ensure that you correctly edit and compile the program and waveform file, as well as the final output.
VHDL Program
ieee library;
use ieee.std_logic_1164.all;
b2g_code entity is
port (b: in std_logic_vector(3 to 0);
g: out std_logic_vector(3 to 0));
end b2g_code;
b2g_arch architecture of b2g_code is
to start
g(3) <=b(3);
g(2) <= b(3) xor b(2);
g(1) <= b(2) xor b(1);
g(0) <= b(1) xor b(0);
end b2g_arch;
It may be helpful to review the first two VHDL tutorials ( 1 and 2 ) in this series to refresh your memory on how this works.
Then compile the above program, creating and saving a waveform file with all required inputs and outputs listed (ensuring all different input combinations apply). Then simulate the project. You should get the following result…
Simulation Waveform

It is easy to check all the different combinations of the binary code input (b0-b3) with the gray code output (g0 – g3). Next, we will do the reverse procedure. We will build a gray code to binary converter circuit.
The gray code to binary converter circuit
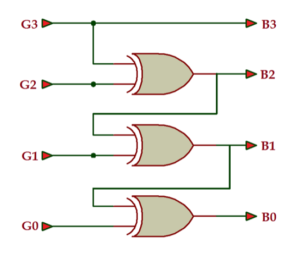
VHDL Program
ieee library;
use ieee.std_logic_1164.all;
g2b_code entity is
port (g: in std_logic_vector(3 to 0);
b: output std_logic_vector(3 to 0));
end g2b_code;
g2b_arch architecture of g2b_code is
to start
b(3) <= g(3);
b(2) <= g(3) xor g(2);
b(1) <= g(3) xou g(2) xou g(1);
b(0) <= g(3) xou g(2) xou g(1) xou g(0);
end g2b_arch;
Simulation waveforms
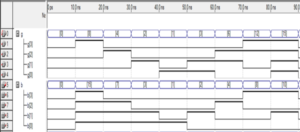
It is clear from the figure that the gray code input (g0 – g3) and the binary code output (b0 – b3) correspond to the given truth table.
In the next tutorial, we will build an 8-bit full adder circuit using VHDL.

