In the previous tutorial, Boolean arithmetic was introduced. It was shown how binary numbers can be added, subtracted, multiplied and divided. In this tutorial, logical operations on binary numbers will now be discussed. Logical operations are not just the way to implement arithmetic operations (through combinational circuits), they form the building blocks of digital circuits. A digital circuit is constructed by logic gates where the logic gates perform one or another Boolean logic operation.
Digital information is stored in a binary cell computing system. A binary cell is a device that can have a logic HIGH or logic LOW state and therefore can store one bit of information. In a positive logic system, the voltage between 2V to 5V as input signal level (on a TTL port) and 2.7V to 5V as output signal level (from a TTL port) is considered as logic HIGH and any voltage between 0V to 0.8V as input signal level (on a TTL port) and 0V to 0.5V as output signal level (from a TTL port) is considered as logic LOW. In a negative logical system, it is vice versa. The voltage levels between HIGH and LOW logic levels are called transition levels and digital circuits (logic gates) do not respond to them.
A group of binary cells is called a record. Registers are used to store digital information in a computing system (processor or microcontroller). There can be 8 bits (8 binary cells in a single register), 16 bits (16 binary cells in a single register), 32 bits (32 binary cells in a single register), or 64 bits (64 binary cells in a single register). ) registers on an 8-bit, 16-bit, 32-bit, or 64-bit computing system, respectively. Digital circuits search for binary information stored in registers and operate on them according to their digital circuits built by logic gates, and then store the result again in other registers.
The binary number stored in a binary cell or record can be treated as a binary or a Boolean variable. Operations on these Boolean variables (formed by the digits 0 and 1) follow a set of mathematical rules that is known as Boolean algebra. Operations on a set of Boolean variables by a digital circuit can be expressed mathematically as a Boolean function. Thus, a Boolean function is formed by binary constants, binary variables and logical operators. The basic logical operations in Boolean algebra are AND, OR, and NOT operations. The AND, OR and NOT operations are performed by AND, OR and NOT logic gates respectively in a digital circuit.

Fig. 1: Representational Image of Boolean Logical Operations
And Operation –
The logical AND operation is equivalent to bit multiplication. If two bits are multiplied, if both bits are 1, only the result will be 1; otherwise, if one of the bits is 0 or both bits are 0, the result is 0. In Boolean algebra, the AND operation is represented by dot or absence operator. Suppose there are two Boolean variables A and B, then the logical AND between A and B is represented by AB or AB. If the result of this AND operation is stored in a variable Y, then it will be written as AB = Y or AB = Y. This will be read as 'A AND B equals Y'. All possible results of AND operation between two single bit variables A and B are shown in the following truth table –
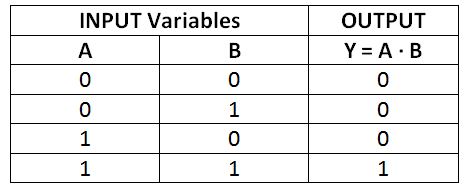
Fig. 2: AND Operation Truth Table
OR Operation –
The logical OR operation is equivalent to adding bits. If two bits are added, if both bits are 0, only the result will be 0; otherwise, if one of the bits is 1 or both bits are 1, the result is 1. In Boolean algebra, the OR operation is represented by the plus operator. Suppose there are two Boolean variables A and B, then the logical OR between A and B is represented by A + B. If the result of this OR operation is stored in a variable Y, then it will be written as A + B = Y. This will be read as 'A OR B equals Y'. All possible results of OR operation between two single bit variables A and B are shown in the following truth table –
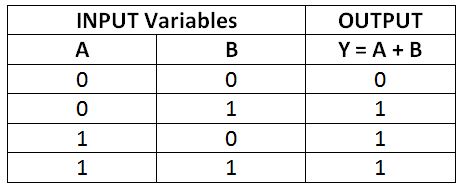
Fig. 3: OR Operation Truth Table
NO Operation –
The NOT operation applies to a single operand. It is equivalent to 1 compliment of a binary variable. If a single-bit Boolean variable has logical state 0, that is NOT operation will result in 1 and vice versa. It is represented by a prime or a top slash. Suppose, if a Boolean variable A is considered as an operand, the NOT operation on it will be represented by A' or Ā. If it is stored in a variable Y, it will be written as A' = Y or Ā = Y. It will be read as 'not A is equal to Y'. Since the not operator inverts the bits of the operand variable, it is also called a logical inverter. All possible results of the NOT operation on a single-bit variable A are shown in the following truth table – NOT Operation –
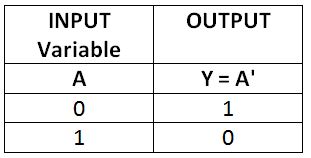
Fig. 4: Truth Table of NOT Operation
Boolean algebra –
Logical operations on Boolean variables follow a set of rules that is known as Boolean algebra. By the rules of Boolean algebra, Boolean variables combined with logical operators (AND, OR and NOT) can be expressed as Boolean functions. AND, OR and NOT are the basic operators of Boolean algebra. Every Boolean algebraic expression (a Boolean function) is always expressed in the form of AND, OR, and NOT operations on Boolean variables. There can be one, two, three, or any number of Boolean variables in a Boolean function or Boolean algebraic expression. Boolean algebra –
Practically, each Boolean variable represents a bit or a serial combination of bits in a computing system. By implementing a series of logical operations on a set of Boolean variables (each variable obtained from a binary cell or record) in a data path, the digital circuit performs computation (binary arithmetic and thus binary algebra) on the input data (represented by boolean variables).
Boolean Addition –
Boolean addition on individual bits is performed by the OR operation. It is governed by the following rules –
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
It can be seen that Boolean addition on two bits is equal to the logical OR operation on them.
Boolean multiplication –
Boolean multiplication on individual bits is performed by the AND operation. It is governed by the following rules –
0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1
It can be seen that Boolean multiplication on two bits is equal to the logical AND operation on them.
Boolean Praise –
The complement of a Boolean variable is performed by the NOT operation. It is governed by the following rules –
0' = 1
1' = 0.
It can be seen that the Boolean praise (praise of 1) on a bit is the same as the logical NOT operation on it.
Now, it should be clear that by implementing logical operations (OR, AND, NOT), arithmetic operations on binary numbers (and therefore on digital data) can be performed. In the next tutorial, learn about multiple logic gates . Logic gates perform basic logical operations (AND, OR, NOT) and other logical operations (derived from AND, OR and NOT). Logic gates are the building blocks of a digital circuit. Any Boolean algebraic expression or Boolean function can be expressed and minimized to basic logical operations between Boolean variables (data obtained through data paths) which can then be practically manufactured in a digital circuit as interconnection between logic gates.

