Leis de indução eletromagnética de Faraday

Faraday's laws of electromagnetic induction

June 23, 2024 Luciano Bertene

Michael Faraday's profound discoveries in the 19th century revolutionized our understanding of electricity and magnetism and laid the foundation for modern technological advances. His most significant contributions were Faraday's groundbreaking laws of electromagnetic induction, which revealed the fundamental relationship between magnetic fields and electric currents. These laws revealed the fascinating interplay between two seemingly disparate phenomena and paved the way for countless innovations that shape our world today.

Laws

Michael Faraday, a British scientist, formulated two laws of electromagnetic induction .

First law

When the number of magnetic lines of force connected to a coil or circuit changes, an electromotive force is induced in that coil or circuit.

When a magnetic field changes across a conductor, an electromotive force (EMF) or voltage is induced in the conductor. The strength of the induced emf is directly proportional to the rate of change of the magnetic field over time. Mathematically, this can be expressed as follows:

emf = -dΦ/dt,

Here EMF is the induced electromotive force, dΦ/dt represents the rate of change of magnetic flux through the conductor and the negative sign indicates that the direction of the induced electromotive force is opposite to the difference in magnetic field.

Second law

Faraday's second law essentially states that the induced electromotive force is determined by the magnetic flux flowing through a closed loop of wire or circuit. When the magnetic field flowing through the circuit changes, an electromotive force is induced in the coil, and when the circuit is closed, a current flows due to this induced electromotive force.

The intensity of the induced electromotive force is directly proportional to the rate of change of the flux bonds.

∴ Flux chains = flux x number of coil turns

The law is explained below:

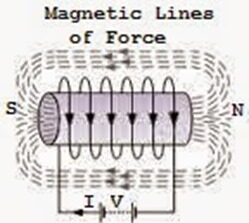
Imagine a coil with N turns.
The initial flow association with a lock is _ф _1.
Initial flow chains = Nф _1.

In the time interval t, the flux ф associated with the coil changes ₁ to ф ₂ .

∴ Final flow chains = Nф ₂ E,

Rate of change of flow links = (Nф ₂ – No ₁ ) /T

According to the first law, an electromotive force is induced in the coil and according to the second law, the intensity of the electromotive force is proportional to the rate of change of the flux bonds.

∴ t ∝ (N ф ₂ -N ф ₁ ) /T

e = K(N ф ₂ -N ф ₁ ) /T

e = N.(d ф /dt)

With K as the unit, you get the unit of e in volts. dф is the change in flow and changes over time. Therefore, (dф/dt) is the rate of change of the river.

Now, according to Lenz's Law, the induced electromotive force produces a current in the opposite direction to the cause that produces it. Mathematically, this resistance is expressed by a negative sign.

Such induced electromotive force is expressed mathematically along with its sign as follows:

∴ E = -N(d ф /dt) Volts

Applications of Faraday's Laws

Faraday's laws form the basis of how many devices and technologies work. Some notable applications are:

Electrical Generators : Electrical generators convert mechanical energy into electrical energy by rotating a coil of wire in a magnetic field, inducing an electromotive force according to Faraday's laws.

Transformers : Transformers use Faraday's laws to transfer electrical energy between different voltage levels by varying the magnetic field and inducing an electromotive force in a secondary coil.

Induction Heating : Induction heating is based on Faraday's laws of generating heat in conductive materials by inducing currents through the materials using alternating magnetic fields.

Magnetic flow meters : These devices measure the flow of electrically conductive fluids by exploiting Faraday's laws to detect the induced voltage caused by fluid movement in a magnetic field.

Connection between magnetism and electricity

The interaction of magnetism and electricity forms the basis of our understanding of electromagnetism, a fundamental force that governs countless natural phenomena. At the heart of this fascinating relationship lies a profound connection in which magnetic fields and electrical currents intertwine, creating a symphony of scientific exploration and technological innovation.

Faraday's Laws, formulated by visionary scientist Michael Faraday, form the cornerstones of our knowledge and provide profound insights into how magnetic fields generate electrical currents and vice versa. These laws revealed the intimate relationship between two seemingly disparate phenomena and paved the way for groundbreaking advances that changed our world.

By unlocking the mysteries of Faraday's laws, we gain a deeper understanding of the intricate dance between magnetism and electricity. We explore the concept of electromagnetic induction, where changing magnetic fields induce electrical currents in conductors, leading to a wide range of practical applications. From power generation and electric motors to magnetic levitation and wireless charging, the implications of this connection are enormous and far-reaching.

Faraday's laws and Maxwell's equations

Faraday's laws played a crucial role in James Clerk's development of Maxwell's equations, which describe the fundamental laws of electromagnetism. Maxwell's equations extended Faraday's laws and integrated them with other basic principles, such as Gauss's law for electric fields and Gauss's law for magnetic fields. Together, these equations form the basis of classical electromagnetic theory.

Faraday's laws of electromagnetic induction are fundamental principles for understanding and applying electromagnetism, form the basis for numerous technologies, and play a central role in the study of electricity and magnetism.