To better understand the functionality and performance of a filter, there are mathematical functions that theoretically represent a filter, such as transfer function, quality factor and cutoff frequency. Understanding these terms will make understanding a filter property easier.
Terminologies (definitions)
Transfer Function: The inputs and outputs of an operational amplifier circuit can be voltages, currents, or a combination of the two. When you use complex numbers for input and output quantities, the relationship between output and input becomes a function of frequency. The name of the reason is transfer function.
Laplace Transform: Laplace transform is used to solve differential equations, Laplace transform converts the differential equation into an algebraic problem which is relatively easy to solve.
Time variant system: the delay or advance of time in the input signal changes not only the output, but also the other parameters.
Transfer function
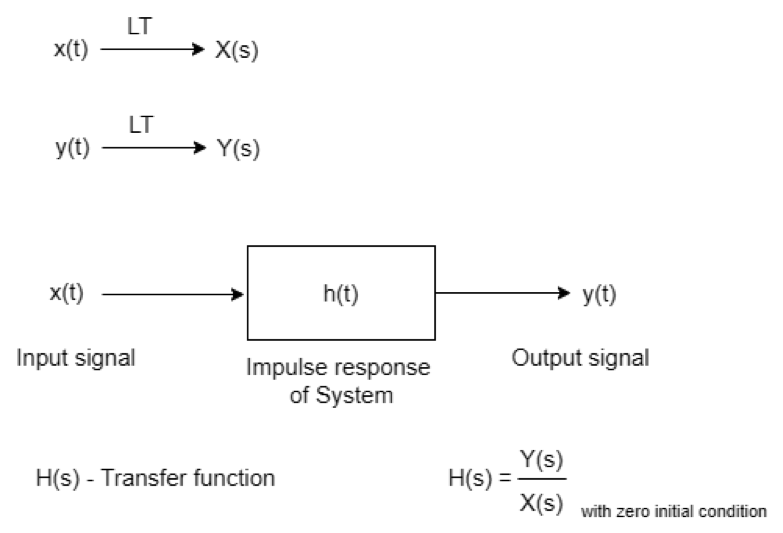
The transfer function is the ratio between the Laplace transform of the output and the Laplace transform of the input when all initial conditions are assumed to be zero. The transfer function cannot be defined if the initial condition is not assumed to be zero.
Zero initial conditions mean that the system must be linear, as time-varying linear systems are used in practice.
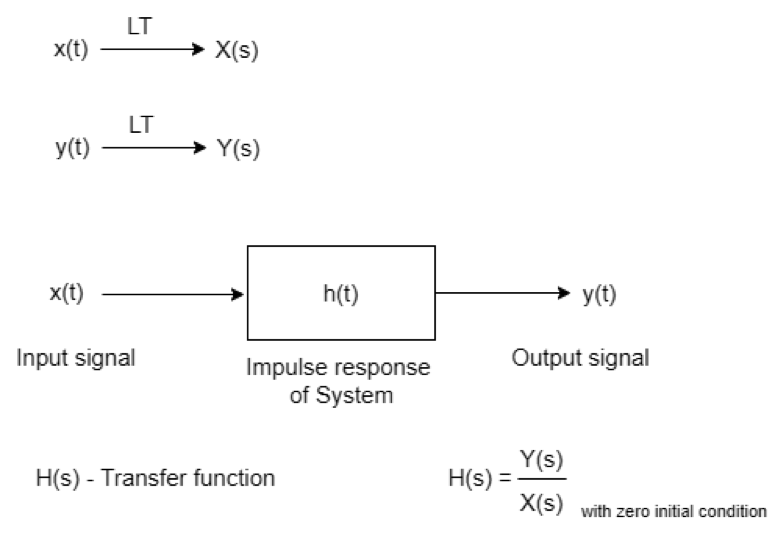
Figure 1 Transfer function block diagram.
Due to the impedance of an inductor or capacitor, filters have a frequency-dependent response that changes with frequency.
Since time-varying signals are used in practice, and these signals pass through a circuit (filtering, amplification, attenuation), there is a possibility that these signals are affected by the components (inductor, capacitor and resistors) used in the the circuit. And filters are used to attenuate some part of the signal frequency.
As we know, w the impedances of a capacitor and an induction, respectively, are
Zc = 1/sC
Z i = sL
Plane S s = ó +jù
The S-plane is a complex plane (having real and imaginary components) in mathematics on which the Laplace transform can be plotted.
Where neper frequency, nepers per second (NP/s)
ù angular frequency (rad/s)
The filter transfer function can be developed using standard circuit analysis techniques. These techniques are Kirchoff's voltage and current laws, Ohm's law and superposition. As we know that impedances are complex, so the transfer function will be
H(s) = I is I + a m-1 is m-1 +…+ a 1 s + a 0 b n is n +b n-1 is n-1 +…+b 1 s + b 0
Where m is the degree of the numerator, n is the degree of the denominator and H(s) is the rational function of s.
The degree of the denominator is called the order of the filter. By solving the above equation, you will obtain roots that determine the zeros (numerator) and poles (denominator) of the filter circuit. Each pole provides a response of -6 dB/octave or -20 dB/decade and each zero provides a response of +6dB/octave or +20 dB/decade. The calculated roots of the transfer function can be real or complex. If they are complex, then the roots are drawn in the s-plane (the complex plane) where the horizontal axis is real (ó,) and the vertical axis is the imaginary axis (ù). The distribution of the roots in the s-plane or complex plane tells us many things about the filter circuit. For stability in the system, all poles must be on the left side of the complex plane. Zero at the origin means there is zero in the numerator, which means the filter will have no DC response.
Let's consider the RLC circuit and write a transfer function for it.

The voltage across the resistor is
H(s) = VoVin = RCsLCs 2 + RCs +1)
If R = 10, L =10mH, C=10uF then substituting the component values.
H(s) = 10 3 x(s 2 + 10 3 s + 10 7 )

After factoring,
H(s) = 10 3 x (s(s-(-0.5+j3,122)x10 3 ) x (s-(-0.5-j3,122)x10 3 ))
The above equation gives a zero at the other origin and pole at:
S = (-0.5±j3.122)x 10 3
The plan above shows these points.
In real applications, in most cases, we are more interested in the performance of the hardware circuit. But we should also look at the s-plane of the filter, Neper and imaginary frequencies.
Cutting frequency (F 0 ) and quality factor (Q)
Working with a plan S is not that convenient, so the question arises why? The answer is: you need to know the transfer function to understand the quality factor and cutoff frequency.
Cutoff frequency (F 0 )
The cutoff frequency is the frequency at which the filter begins to filter the signal, so the cutoff frequency in a low-pass filter is the frequency at which the filter begins to remove high frequencies, the cutoff frequency it's actually the point where the output level is 3 dB lower than the input level, so it's not exactly the point where the filter starts to work.

The cutoff frequency is a limit on the frequency response of a system; the energy flowing through the system begins to be reduced, attenuated, or reflected instead of passing through. Typically, in electronic systems such as filters and communication channels, the cutoff frequency applies to an edge in the low-pass, high-pass, band-pass, or band-stop characteristics of a frequency that characterizes a boundary between the passband and the final band. It is sometimes taken to the point in the filter response where the transition band and passband meet.
The cutoff frequency is generally defined as the frequency at which the filter response is 3dB below the passband. The frequency at which the ratio (output/input) has a magnitude of 0.707. If you convert this magnitude to decibels, you get -3dB, which means a negative 3dB point.
dB = 20 log (0.707)
The amount of filter attenuation begins to increase rapidly at this point, as shown in the figure below.

Quality factor (Q)
The quality factor is a measure of the filter peak. Q is really only valid for the second order filter and is not valid for first or third order systems. The quality factor is defined as the potential drop across the inductor or capacitor to the potential drop across the resistor.
Q = (Voltage drop across “L”) / (voltage drop across “R”)
Or
Q = (voltage drop across “C”) / (voltage drop across “R”)
Calculation of quality factor for inductor:
Q = (I X I ) / (I R)
Q = X L / R = wL / R
Q = 2pfL/R
f is the resonance frequency, f = 1/2p sqrt (LC)
Q = (1/R) square(L/C)
Similarly, the quality factor of a capacitor is also calculated, which is also,
Q = (1/R) square(L/C)
For an RC, LR or RLC circuit, the transfer function will be the same as the equation above.
The quality factor is how underdamped a resonator is, meaning how quickly an oscillation disappears.
Q is the quality factor, and the quality factor transformation function is expressed as
α = 1/Q
If Q > 0.707, there will be a peak in the filter response.
If Q < 0.707, roll in f 0 will be larger.