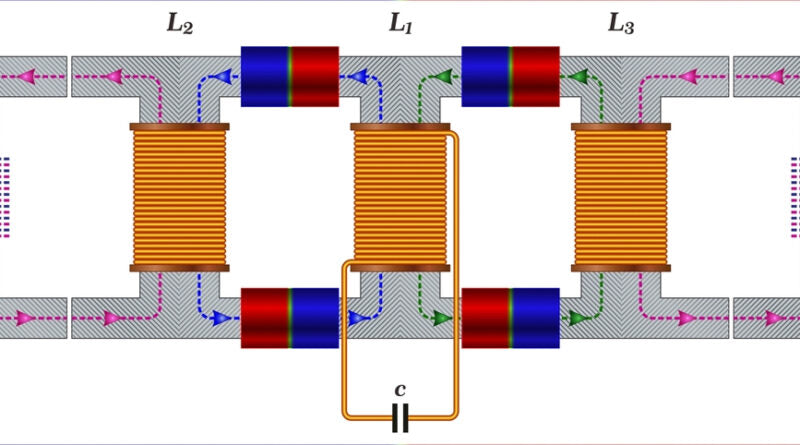
The phenomenon of electromagnetic induction is at the heart of how transformers work, and the EMF equation serves as a fundamental concept for understanding how they work. Transformers are ubiquitous devices in electrical power systems, used for voltage conversion, power distribution, and numerous other applications. The EMF equation establishes an important relationship between the induced electromotive force (EMF) and the magnetic flux within the transformer. Understanding this equation provides engineers and analysts with valuable information about transformer performance, efficiency, and voltage regulation so they can design and optimize these essential electrical components. In this article, we will explore the importance of the EMF equation and how it contributes to the understanding and advancement of transformer technology.
The importance of the EMF equation in transformers
The EMF equation is a fundamental concept at the heart of transformers and plays a crucial role in their operation. It provides insights into the relationship between induced electromotive force (EMF) and magnetic flux in the transformer. Understanding the EMF equation is critical to transformer design and analysis as it helps evaluate their voltage regulation, efficiency, and overall performance.

Faraday's law of electromagnetic induction
Faraday's law of electromagnetic induction forms the core of the EMF equation. This law states that a changing magnetic field induces a voltage in a conductor. In transformers, alternating current flowing through the primary winding creates a changing magnetic field that causes an EMF in the primary and secondary windings.

- Faraday's law of electromagnetic induction is a fundamental principle of electromagnetism discovered by physicist Michael Faraday in the early 19th century.
- It describes the relationship between a changing magnetic field and the induction of an electromotive force (EMF) in a conductor.
- Faraday's law forms the basis for understanding how various electrical devices, including transformers, generators, and motors, work.
- Faraday's first law states that when the intensity or direction of a magnetic field changes relative to a conductor, an electromotive force is induced in the conductor.
- The induced electromotive force is proportional to the rate of change of the magnetic field over time.
- This law is represented mathematically as follows: EMF = -dΦ/dt, where EMF is the electromotive force, dΦ/dt represents the rate of variation of the magnetic flux and the negative sign indicates the direction of the induced current.
- To understand Faraday's law, it is important to understand the concept of magnetic flux.
- Magnetic flux (Φ) is the measurement of the magnetic field that flows through a given area perpendicular to the field.
- It results from the product of the intensity of the magnetic field (B) and the area (A) perpendicular to the field: Φ = B * A. which is equal to 1 Tesla (T) multiplied by 1 square meter (m²).
- Faraday's second law, also known as the law of electromagnetic induction, expands the understanding of Faraday's first law.
- Indicates the magnitude of the change in the magnetic flux connecting the conductor.
- Mathematically, it can be expressed as follows: EMF = -dΦ/dt, where EMF is the electromotive force and dΦ/dt represents the rate of variation of the magnetic flux.
Induced electromotive force in transformers
The emf equation describes the relationship between the induced emf and the magnetic flux in the transformer. As the magnetic flux connecting the windings changes due to the alternating current, it creates a corresponding emf in the windings. This induced emf transfers electrical energy from the primary winding to the secondary winding of the transformer.

Factors Affecting the EMF Equation
Several factors influence the EMF equation in transformers. The number of turns in the primary and secondary windings, magnetic flux density, and AC frequency are key factors that affect the intensity of the induced EMF. Changing these factors can affect the transformer's performance characteristics, such as: B. voltage transmission ratio and efficiency.
Transformer design and analysis
The EMF equation is critical to transformer design and analysis. Engineers use the EMF equation to determine the required number of turns in the windings, select appropriate core materials, and optimize the transformer for specific applications. By considering the EMF equation, designers can ensure the transformer meets desired voltage regulation, efficiency, and other performance criteria.
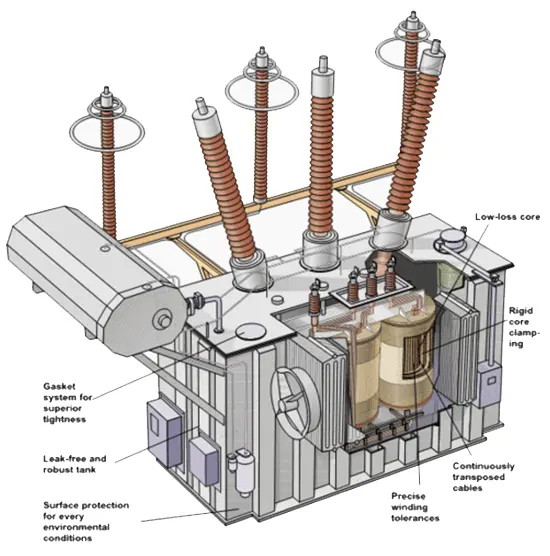
To leave,
N 1 = Number of turns in the primary winding
N 2 = Number of turns in the secondary winding
Φ M = Maximum flux in the core in Webers
=B M x A
F = AC input frequency in Hz.
In the figure, the flow increases from zero to the maximum Φ M Value in a quarter of the cycle, that is, in 1/4 f second.
∴ The average rate of change of flow = Φm /1/4f
= 4 Wb/s or volts
The rate of change of flux per revolution means the induced electromotive force in volts.
∴ Average electromotive force/revolution = 4 f Φ M volt
If the flux Φ varies sinusoidally, then the effective value of the induced electromotive force is determined by multiplying the average value by the shape factor.
Form factor = RMS value / average value = 1.11
∴ RMS value of electromotive force/revolution = 1.11 × 4 f Φ M
= 4.44fΦ M Volt.
Well, RMS value of the electromotive force induced across the primary winding
= (electromotive force/induced revolution) × number of primary revolutions
E1 = 4.44fN 1 Φ M = 4.44fN 1 b M Um —>1
Likewise, the effective value of the electromotive force induced in the secondary winding is:
E2 = 4.44fN2Φ M = 4.44fN 2 b M ON —->2
From equation 1 -> 2 it follows that E 1 /N 1 =E 2 /N 2 = 4.44fΦ M .
This means that the electromotive force/turn in the primary and secondary windings is the same.
In an ideal no-load transformer, V is 1 =E 1 and E 2 = V 2 Where V 2 is the terminal voltage
Conclusion
A deep understanding of the EMF equation has led to significant advances in transformer technology. Engineers have explored innovative designs such as resonant and multi-winding transformers that improve efficiency, compactness and versatility. These advances have enabled the integration of transformers into new technologies, including smart grids, renewable energy systems and electric vehicle charging infrastructure.
Related article
PN junction diode
Common questions
What is the emf equation of a transformer?
The emf equation of a transformer is represented by the formula e = 4.44fnφ, where:
and is the induced electromotive force (EMF) in volts,
f is the network frequency in Hertz (Hz),
n is the number of turns in the coil and
φ is the magnetic flux in Webers (Wb).
How to calculate the RMS value of the voltage induced in a transformer?
To calculate the RMS (Root Mean Square) value of the induced voltage in a transformer, you can use the following formula: Vrms = (e / √2), where e is the induced electromotive force given by the electromotive force equation (e = 4 ,44fnφ) is given.
What are the main factors that affect voltage drop across a transformer?
The voltage drop across a transformer is affected by several factors, including:
Resistance of the transformer coil and its windings
Load current through transformer
Leakage reactance and reactance change in transformer
How important is power factor in transformer operation?
Power factor plays a crucial role in transformer operation as it represents the phase difference between voltage and current in the system. A low power factor can lead to higher losses, reduced efficiency and increased voltage drop across the transformer.
How does an induction motor based on the principles of electromagnetic induction work?
An induction motor works on the principle of electromagnetic induction. When the stator windings are supplied with alternating current, a rotating magnetic field is created, which induces a voltage in the rotor windings. This induced voltage causes the rotor to rotate and drives the mechanical load of the motor.