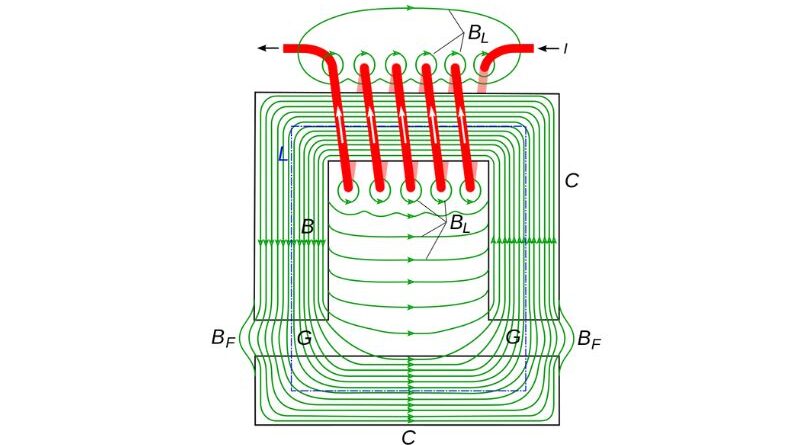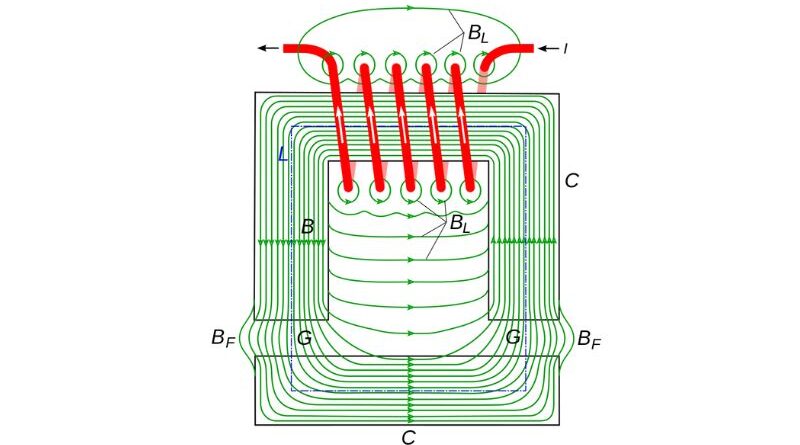
Magnetism has been a fascinating force since ancient times. Early civilizations were fascinated by the properties of magnets and used magnetic compasses for navigation. But it was not until the 16th century that William Gilbert established magnetism as a science with his pioneering work. His influential book “De Magnete” laid the foundation for understanding the magnetic field and its behavior. Since then, the study of magnetism has evolved, leading to the discovery of fundamental laws and principles that govern magnetic circuits and their application in various technological advances.
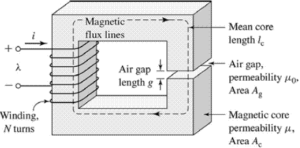
Magnetic Circuit Calculations
Magnetic circuitry forms the backbone of various electrical and electronic devices and allows for the efficient transmission and use of magnetic energy. Deciphering the fundamental laws that govern the magnetic circuit is crucial to understanding and optimizing these systems. It has been discovered that the laws governing the constant flow of current in a course can be easily changed. To be immediately applicable to the Magnetic Circuit . Therefore
Magnetomotive driving force = flux x reluctance
F = ΦxS
Exactly corresponds to electromotive force = current x resistance
Reluctance = (Length/Area) x (1/Permeability)
= l/Aµ
For a magnet with a uniform cross-sectional area that exactly matches
Resistance = (Length/Area) x (1/Conductivity)
It is often convenient to calculate in unit dimensions. We then have
mmf per unit length = flux x reluctance per unit length
= (flow/area) x (l/permeability)
= flux density x (l/permeability)
Magnetic field intensity H = B/µ
This corresponds exactly to
For a material with uniformly distributed flow and length l, the total mmf is equal to the mmf per unit length xl
i.e. F=Hl or AT=Hl
By dealing with the Magnetic Circuit where the flux must pass through several different parts in seconds, the methods used to deal with electrical circuits in series can be applied immediately, the total reluctance being the sum of the values of the different parts. Normally, the importance of reluctance is only significant to the extent that it allows determining the mmf necessary to produce a given flow in the circuit. The simplest method is usually to determine this total mmf value by adding the mmf values needed to produce flow through the various parts of the circuit. This is exactly the same as calculating the total voltage drop in an electrical circuit by adding the voltage drop values across the different parts.
Thus, the total value of the mmf around a complete magnetic field is given by
AT (or) F = ∫Hdl
Or if the circuit consists of several homogeneous parts, each of which has a uniform cross-section and length 1 L 2 etc.
total mmf F (or) AT = Σ Hl = H 1 1 1 +H 2 I 2 +….
= Φ (p 1 +S 2 +….)
If the values of the area and permeability of the different parts of the circuits are A 1 μ 1 etc. becomes all MMF
AT (or) F = (B 1 /μ 1 )i 1 + (B 2 /μ 2 )i 2 +…..
Where B 1 =Φ/A 1 etc.
Occasionally it is convenient to express the basic law of the magnetic circuit in form.
Flux = magnetomotive force x permeance
Permeability is nothing more than the reciprocal of Restriction treating paths in parallel; the total permeance is the sum of the values of the individual paths.
The main difference between electrical and magnetic calculations arises from the fact that the resistance of an electrical circuit does not directly depend on the value of the reluctance of a magnetic substance, but to a large extent on the value of the flux passing through it.
The magnetic field and magnetic flux
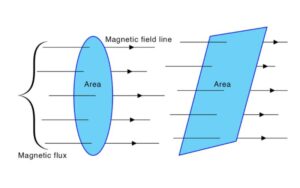
Understanding the magnetic field is crucial to understanding how magnets interact with each other and with other objects. The concept of a magnetic field is visually represented by Faraday lines of force, which indicate the direction and strength of the magnetic field. Magnetic flux, the measurement of a magnetic field passing through a surface, is fundamental to understanding magnetic interactions. The calculation of magnetic flux is essential for several applications, mainly in magnetic circuits and transformers.
Ampere's law of circulation
André-Marie Ampère's contributions revolutionized the understanding of electromagnetism. His experiments with current-carrying conductors led to the formulation of Ampere's circuit law, which establishes the relationship between magnetic fields and electric currents. The law provides a fundamental tool for analyzing magnetic circuits and calculating the magnetic field generated by current-carrying conductors. Ampere's circuit law laid the foundation for future advances in electromagnetism.
Magnetic induction and Faraday's law
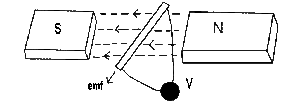
Michael Faraday's groundbreaking experiments on electromagnetic induction marked a turning point in electromagnetism. Faraday's law states that a changing magnetic field induces an electromotive force (EMF) in a conductor. This discovery paved the way for the development of inductive components, such as transformers and inductors, essential in modern electrical systems.
The BH curve and hysteresis
The BH curve represents the relationship between magnetic induction (B) and magnetic field intensity (H) in a magnetic material. Understanding the BH curve is important for predicting the behavior of magnetic materials under varying magnetic fields. Hysteresis refers to the phenomenon that a magnetic material retains residual magnetism even after the applied magnetic field is removed. This behavior leads to energy losses in magnetic circuits and minimizing hysteresis effects is crucial for efficient operation.
Magnetic Circuit Analysis
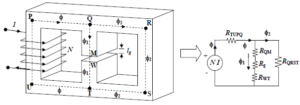
Magnetic circuits can be analyzed using similar principles as electrical circuits. The corresponding models and courses simplify complex magnetic systems and make it easier to study and understand their behavior. Parameters such as magnetic field strength, magnetic flux and magnetic resistance are calculated to evaluate and optimize magnetic circuits. Kirchhoff's laws, adopted from the analysis of electrical circuits, are applied to magnetic circuits to solve practical problems.
Applications of magnetic circuits
Magnetic circuits have a wide range of applications in modern technology. Electric motors and generators use magnetic circuits to convert electrical energy into mechanical work and vice versa. Magnetic sensors use principles such as the Hall effect and find applications in a variety of industries, including automotive, medical and consumer electronics. Magnetic shielding is essential for protecting sensitive electronic devices from electromagnetic interference (EMI) caused by external magnetic fields.