Welcome to the fascinating world where the symphony of electricity and magnetism performs a complicated dance known as the “Dance of Self-Induced Electromotive Forces in the Magnetic Realm: Electric Symphony”. In this fascinating area, the laws of electromagnetism converge, creating a phenomenon that goes beyond the bounds of the ordinary. Here, the interplay between changing magnetic fields and induced electromotive forces creates a choreography that surprises and illuminates. Just as a conductor leads an orchestra, magnetic fields orchestrate a ballet of details that produce self-induced electromotive forces. This fascinating effect resonates across numerous electrical devices and systems. As we embark on this journey, we peel back the layers of this phenomenon and explore its principles, implications and applications, from energy generation to the heart of our technological landscape. Join us to experience the harmonious convergence of science and art, where the enigmatic dance of self-induced electromotive forces unfolds across the magnetic tapestry of our electrified world.
Induced electromotive force and Faraday's law in coils
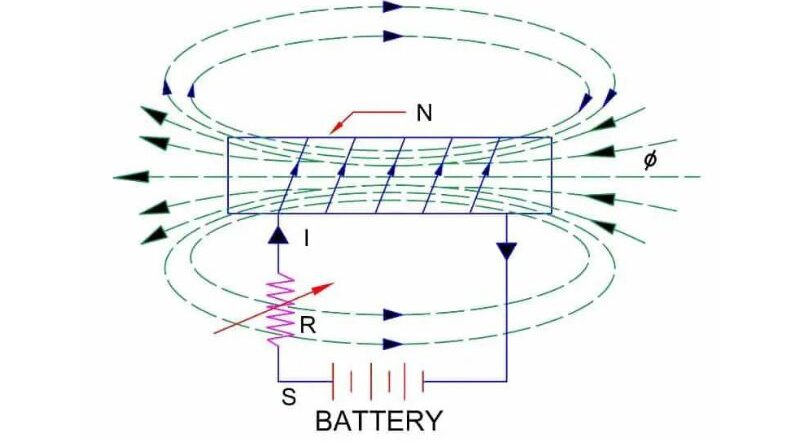
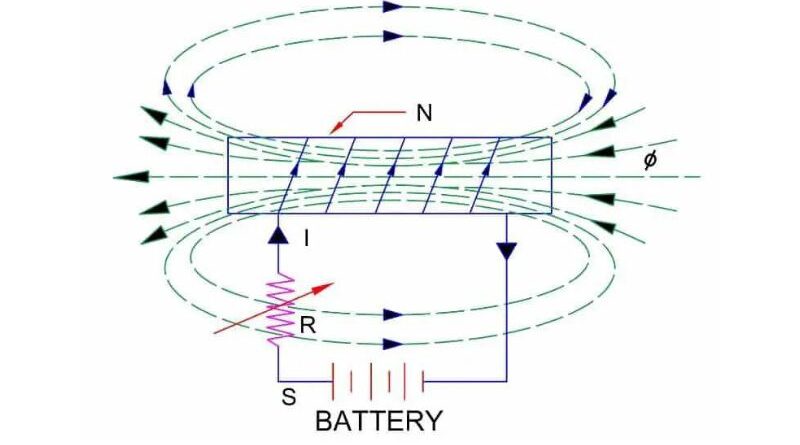
Imagine a multiturn coil carrying current “I” when the key is locked. The current is varied using a variable resistor connected non-parallel (in series) to the battery, coil and controller as shown in the figure.
The flux created by the coil is connected to the coil itself. The total flow links of the ring will be N turns of the network. If the current “I” is changed using a variable resistor, the flux produced can also change because the flux connections also change.
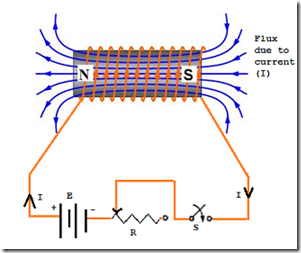According to Faraday's law, an induced electromotive force arises in the coil as a result of the rate of change of the flux connections. Therefore, when the coil or flux is not in physical motion, an induced electromotive force is created in the coil. This development is called self-induction.Self-inductance and Lenz's law in coils
The properties of the coil that resist any change in the current flowing through it are called self-inductance. According to Lenz's law, the direction of this induced electromotive force is opposite to the cause that generates it. The reason for this is that current I, that is, the self-induced electromotive force, tries to find a wind that is in the opposite direction to its current I. Once the current is present, the self-induced electromotive force reduces the current and try to keep it at its original value. As the current decreases, the self-induced electromotive force will simultaneously increase, trying to keep it back to its true value. Thus, any change in current through the coil is prevented by the ring. The magnitude of self-induced EMF 
According to Faraday's law of induction of magnetism, the self-induced electromotive force is expressed as follows:
E = -N (dΦ/dt)
A negative sign means that the direction of this electromotive force counteracts an existing change in current.
The flow is expressed as follows:
Φ = (Flow / Amps) x Amps = (Φ/I) x I
As long as the permeability µ is constant in a circuit, the relationship between flux and current (i.e., B/H) remains stable.
Flow rate of change = (Φ/I) x current rate of change.
∴ (dΦ/dt) = (Φ/I) x (dI/dt)
e = -N(Φ/I)x(dI/dt)
e = -(NΦ/I)x(dI/dt)
The constant NΦ/I in this expression is nothing. However, quantitative measurement of the coil property counteracts any change in current.
Therefore, this constant NΦ/I is called the self-induction coefficient constant and is labeled “L”.
It is given as auxiliary connections per ampere current. The unit is Henry (H).
A circuit has a self-induction coefficient of 1 H as soon as a current of 1 Ampere flows through it and creates flux chains of 1 Wb-tum in it.
∴ e =-L (dI/dt) volts
The self-induction coefficient can be determined from this equation.
L = (NΦ/I)
But Φ = (mmf/reluctance) = NI/S
L = N.NI/IS
l = N 2 /Sh
Now S=l/µa
l = N 2 / (l/µa)
l = N 2 µa/l = (N2 µ 0 μ R a/l) Henries
Where l = length of the magnetic circuit
A = Cross-sectional area of the magnetic circuit through which the flux flows.
Self-induced EMF
The self-induced EMF mechanism
Self-induced electromotive force (EMF) in magnetic circuits arises from changes in magnetic flux within a circuit that result in the generation of voltage. This subsection focuses on understanding the basic mechanism behind self-induced electromotive force and examines concepts such as Faraday's law of electromagnetic induction and Lenz's law.
Effects and applications of self-induced EMF
This subheading deals with the practical implications and applications of self-induced electromotive force in magnetic circuits. Discusses how self-induced electromotive force can neutralize or assist the original current, resulting in different effects. In addition, several applications of self-induced electromotive force are examined, including its importance in power generation, transformers, electric motors and generators.
Conclusion
At the end of our exploration of the dance of self-induced electromotive forces in the magnetic domain, we can further appreciate the elegance of this complex interaction. Faraday and Lenz's laws revealed a captivating choreography that showed how current fluctuations and induced electromotive forces unexpectedly harmonize. The concept of self-inductance provides a powerful understanding that drives innovation in areas such as power generation and transformers. This electric symphony reminds us of the beauty of understanding the forces that shape our technological landscape. As we finish this journey, we want to take our newly acquired knowledge with us to further unravel the mysteries of the dynamic relationship between electricity and magnetism.
FAQs: Self-Induced Electromotive Force in Magnetic Circuits
1. What is self-induced electromotive force (EMF)?
Self-induced electromotive force refers to the voltage induced in a coil or circuit due to changes in the magnetic field within the same circuit. It is a phenomenon governed by Faraday's law of electromagnetic induction.
2. How are self-induced EMFs created?
When the magnetic flux inside a coil changes due to different currents or external influences, an electromotive force induced in the coil itself arises. This phenomenon is based on the principles of electromagnetic induction and self-inductance.
3. What is the role of Lenz's law in self-induced electromotive disturbances?
Lenz's law states that the direction of the induced electromotive force always opposes the change it causes. In the case of a self-induced electromotive force, the induced voltage counteracts any changes in current in the circuit.
4. What is self-inductance
Self-inductance is a property of a circuit or coil that quantifies its ability to resist current fluctuations. Essentially, it is the resistance of the circuit to changes in its magnetic field.
5. How do self-induced EMFs affect current changes?
The self-induced electromotive force can support or neutralize the original current in the circuit. When the current changes, the induced electromotive force helps maintain the current's true value or tries to counteract the change, according to Lenz's law.
