In the first tutorial in this series – Introduction to Digital Electronics, it was mentioned that there are different code systems that are used to represent digital information as binary numbers. Each code system has different binary numbers assigned to the same symbols and characters. Different digital systems can use different code systems. In this case, some code conversion circuitry must remain to make interconnected digital systems compatible.
In this tutorial, code conversion circuits will be designed using SN7400 series of digital ICs. In the previous tutorial, the same series of digital ICs were used to build arithmetic circuits such as half adder, full adder, half subtractor and full subtractor. In this tutorial, the following code conversion circuits will be designed –
· Binary to Gray code converter
· Gray code to binary converter
· Excess BCD – 3-code converter
· Excess – code 3 to BCD converter
The code conversion circuits designed in this tutorial will be used for converting the digits 0 to 9 from one code system to another. Different code systems have different binary numbers assigned to digits. As in gray code, binary numbers are ordered such that any two successive digits or values differ by only one bit. The BCD numbering system is similar to the binary representation of decimal numbers, except that the encoded number is separated into four bits for each digit of the decimal number. Therefore, the encoded number is represented by weighted binary values where each value is 4 bits long and is a direct representation of the digits of the decimal number. The Excess-3 code is similar to the BCD numbering system, with the only difference being that each 4-bit long value in the encoded number is obtained by adding 3 to the BCD representation. The following table summarizes the binary representation of digits 0 to 9 in different code systems –
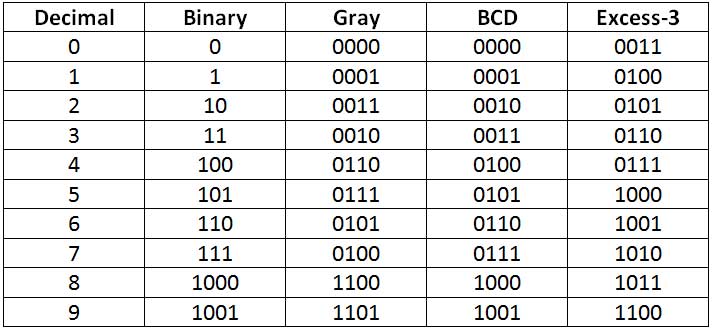
Fig. 1: Table listing binary, gray, BCD and Express-3 encoding for decimal digits
With the knowledge of these code systems, let's now start building the code converter circuits.
Required components –

Fig. 2: List of components required to make SN-7400 series IC-based code converters
Circuit Diagrams –
The binary to gray code converter has the following circuit diagram –

Fig. 3: Circuit Diagram of Binary to Gray Code Converter
The gray code to binary converter has the following circuit diagram –

Fig. 4: Gray code to binary converter circuit diagram
The BCD to excess code converter – 3 has the following circuit diagram –
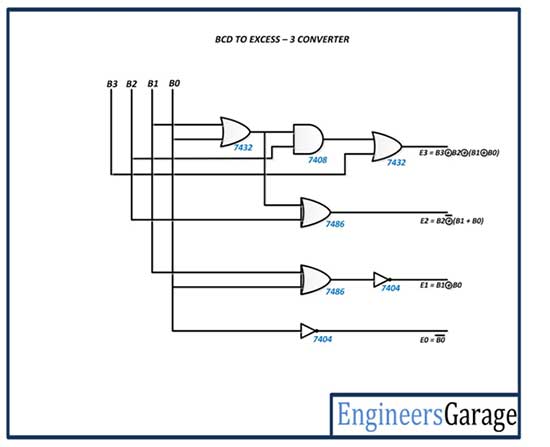
Fig. 5: BCD to Excess 3 Converter Circuit Diagram
The Excess – 3 to BCD code converter has the following circuit diagram –

Fig. 6: Excess Code 3 to BCD Converter Combinational Circuit
Circuit Connections –
The code converter circuits designed in this tutorial are combinational circuits as their output depends only on the current input values. Each circuit has a unique truth table from which the respective Boolean expression for each output can be derived. The minimized Boolean expression is then converted into a logic gate diagram which is built on a breadboard using 7400 series ICs.
The following logic gate ICs are used in constructing the circuits –
7408 IC – The 7408 IC has 2-input quadruple AND gates. The IC has the following pin configuration –
Fig. 7: Circuit Diagram of Excess Converter 3 to BCD Code
The IC has the following pin diagram –
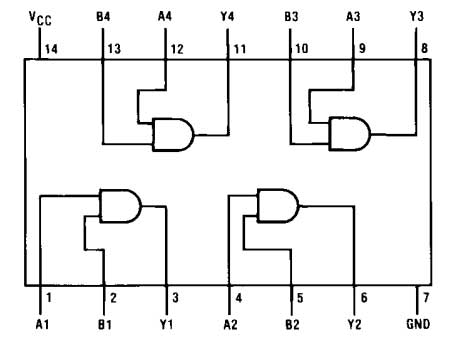
Fig. 8: Pin diagram of 7408 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the AND gate inputs must be 2V for logic high and 0V for logic low. The output of the AND gates has a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on a positive logic system. The propagation delay during transit from LOW to HIGH at the output is 27 ns, while the propagation delay during transit from HIGH to LOW at the output is 19 ns.
7432 IC – The 7432 IC has 2-input quadruple OR gates. The IC has the following pin configuration –

Fig. 9: Table listing the pin configuration of the 7432 IC
The IC has the following pin diagram –

Fig. 10: Pin Diagram of 7432 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the OR gates must be 2V for logic high and 0V for logic low. The output of the OR gates has a voltage of 3.4 V for logic high and 0.35 V for logic low. The IC operates on a positive logic system. The propagation delay during transit from LOW to HIGH at the output is 3 to 15 ns, while the propagation delay during transit from HIGH to LOW at the output is also 3 to 15 ns.
7486 IC – The 7486 IC has 2-input quad EX-OR gates. The IC has the following pin configuration –

Fig. 11: Table listing the pin configuration of the 7486 IC
The IC has the following pin diagram –
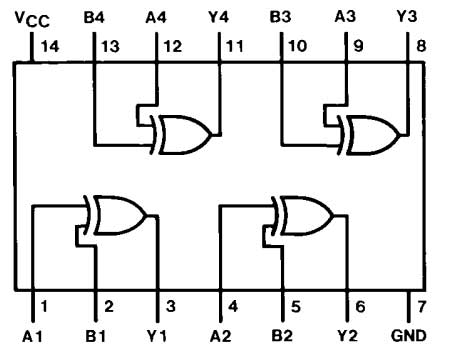
Fig. 12: Pin Diagram of 7486 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the EX-OR gates must be 2V for logic high and 0V for logic low. The output of the EX-OR gates has a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on a positive logic system. The propagation delay during the transition from LOW to HI at the output is 23 ns if other inputs are low and 30 ns if other inputs are high, while the propagation delay during the transition from HI to LOW at the output is 17 ns if other inputs are low and 22 ns if other inputs are high.
7404 IC – The 7404 IC has six inverter ports. The IC has the following pin configuration –

Fig. 13: Table listing the pin configuration of the 7404 IC
The IC has the following pin diagram –

Fig. 14: Pin Diagram of 7404 IC
The IC requires a supply voltage of 5V which can be tolerated up to 7V. The voltage at the inputs of the NOT gates must be 2 V for logic high and 0.8 V for logic low. The output of the NOT gates will have a voltage of 3.4 V for logic high and 0.2 V for logic low. The IC operates on positive logic system. The propagation delay during transit from LOW to HIGH level at the output is 22 ns, while the propagation delay during transit from HIGH to LOW level at the output is 15 ns.
It should be noted that the selected ICs have compatible input, output and power voltage levels as they are taken from a common family (74XX series) of digital ICs.
How the circuit works –
There are different code systems available for representing digital information. Digital systems often use components that can use different code systems. In this case, there must be some code converter circuit between such components, so that they can communicate digital information between them. Commonly used code systems include Gray code, BCD, and Excess-3. In all of these code systems, each binary digit is represented by a unique 4-bit value. For convenience, the binary input to the binary-to-gray code converter and the binary output to the gray-to-binary code converter are also 4 bits long.
Thus, since each code uses four bits to represent a decimal digit, there are four inputs and four outputs. It should be noted that Gray code is an unweighted code while BCD and Excess-3 are weighted code systems. In BCD and Excess-3 code converters, the circuit is designed for single digit conversion only. The input variables are designated as B3, B2, B1, B0 and the output variables are designated as G3, G2, G1, G0. From the truth table, the K-maps for each of the four outputs of the respective circuits are obtained and Boolean functions involving four input variables for each output variable are derived. A two-level logic diagram is obtained directly from the Boolean expressions derived from the maps and combinational circuits are designed for each variable in the respective circuits.
Binary to Gray Code Converter –
Binary numbers are unweighted representations of decimal numbers in base 2. Gray code which is also called Reflected Binary Code (RBC) or just Reflected Binary (RB) has binary numbers ordered to the decimal digits in such a way that any two successive the values differ by only one bit. Gray code is widely used in digital communication systems for error correction. The input binary numbers here are considered to be 4 bits long. To derive the gray code equivalent to binary numbers, first the MSB (Most Significant Bit) is noted as is, then each lower digit in the gray code number is obtained by adding the respective bit and the bit one position lower in the binary number. The circuit has four inputs ( B3 B2 B1 B0) representing 4-bit binary numbers and four outputs (G3 G2 G1 G0) representing 4-bit gray code. The converter circuit has the following truth table –

Fig. 15: Truth Table of the Binary to Gray Code Converter
From the above truth table, the following K-Maps for the output variables are obtained –

Fig. 16: K-Map for G3 in binary to gray code converter
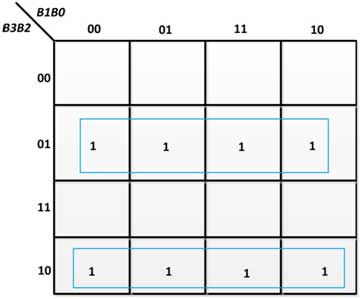
Fig. 17: K-Map for G2 in binary to gray code converter

Fig. 18: K-Map for G1 in binary to gray code converter
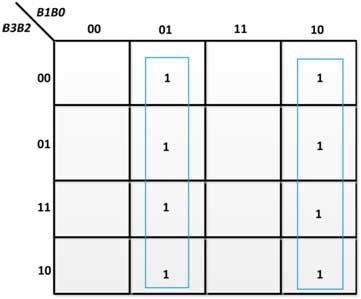
Fig. 19: K-Map for G0 in binary to gray code converter
From the above K-maps, the following Boolean expressions are obtained for the output variables –
G3 = B3
G2 = B3  B2
B2
G1 = B2  B1
B1
G0 = B1  B0
B0
Therefore, the binary to gray code converter digital circuit uses EX-OR gates. It can be built using 7486 IC.
Gray code to binary converter
For conversion from gray code to binary, the MSB is written as is and the subsequent bits are obtained by adding MSB (or high position bit in the converted binary number) and the respective bit in the gray coded number. The circuit has four inputs (G3 G2 G1 G0) representing 4-bit gray code and four outputs (B3 B2 B1 B0) representing 4-bit binary numbers. The converter circuit has the following truth table –
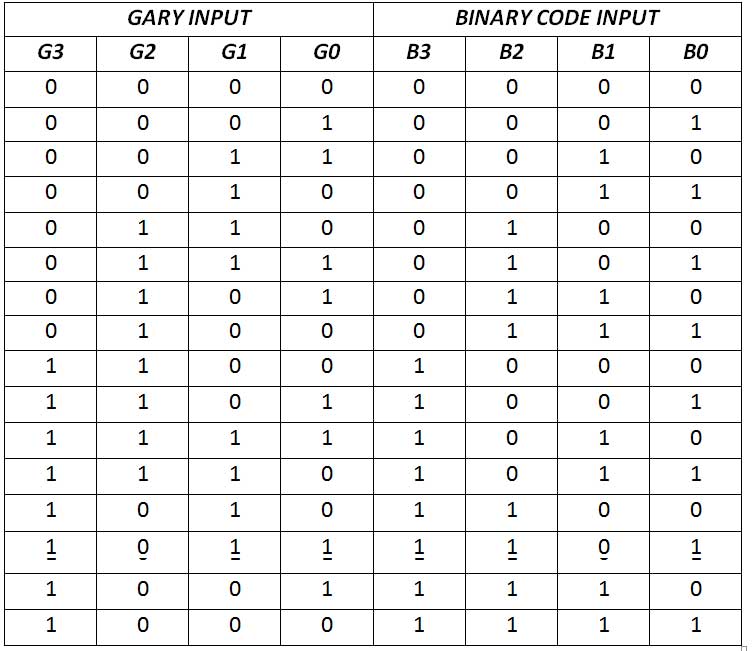
Fig. 20: Gray Code to Binary Converter Truth Table
From the above truth table, the following K-Maps for the output variables are obtained –

Fig. 21: K-Map for B3 in gray code to binary converter

Figure 22: K-Map for B2 in Gray Code to Binary Converter

Figure 23: K-Map for B1 in gray code to binary converter

Figure 24: K-Map to B0 in Gray Code to Binary Converter
From the above K-maps, the following Boolean expressions are obtained for the output variables –
B3 = G3
B2 = G3  G2
G2
B1 = G3  G2
G2  G1
G1
B0 = G3  G2
G2  G1
G1  G0
G0
Therefore, the gray code to binary converter digital circuit uses EX-OR gates. It can be built using 7486 IC.
BCD to Excess-3 Converter
4-bit BCD numbers are the same as 4-bit binary numbers. Numbers encoded in excess of 3 are added 3 to each BCD number. Both BCD and Excess-3 are weighted code systems. The circuit designed here converts only single-digit BCD numbers to equivalent single-digit Excess-3 numbers. The circuit has four inputs (B3 B2 B1 B0) representing 4-bit BCD code and four outputs (E3 E2 E1 E0) representing 4-bit excess – 3 numbers. The converter circuit has the following truth table –

Fig. 25: Truth Table of the BCD to Excess-3 Converter
From the above truth table, the following K-Maps for the output variables are obtained –
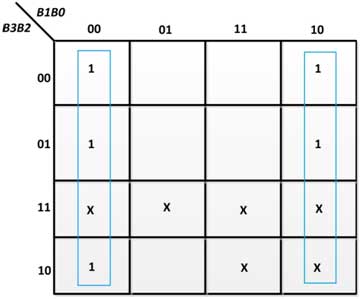
Figure 26: K-Map for E0 in BCD to Excess-3 Code Converter

Figure 27: K-Map for E1 in BCD to Excess-3 Code Converter

Figure 28: K-Map for E2 in BCD to Excess-3 Code Converter
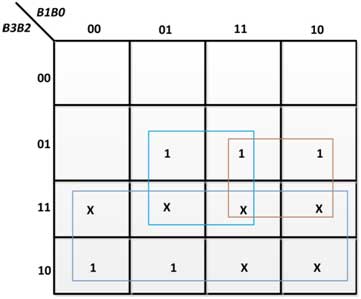
Figure 29: K-Map to E3 in BCD to Excess-3 Code Converter
From the above K-maps, the following Boolean expressions are obtained for the output variables –
E0 = B0'
E1 =B1  B0
B0
E2 = B2  (B1 + B0)
(B1 + B0)
E3 = B3  B2
B2  (B1
(B1  B0)
B0)
Therefore, the BCD to excess 3 code converter digital circuit uses EX-OR, AND, and NOT gates. It can be built using ICs 7486, 7432, 7408 and 7404.
Excess-3 to BCD Converter
BCD encoded numbers are three fewer than Excess-3 encoded numbers. The converter circuit has four inputs (X3 X2 X1 X0) representing 4-bit excess – 3 codes and four outputs (ABCD) representing 4-bit BCD numbers. There is the following truth table –
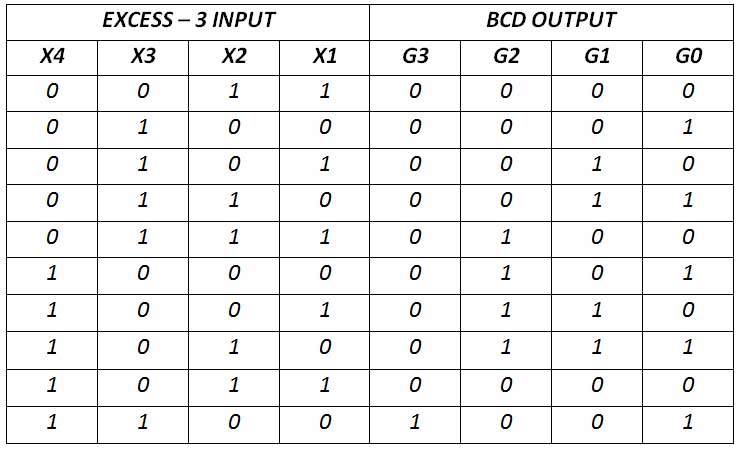
Fig. 30: Excess-3 Converter Truth Table for BCD Code
From the above truth table, the following K-Maps for the output variables are obtained –

Figure 31: K-Map to A in excess-3 to BCD code converter
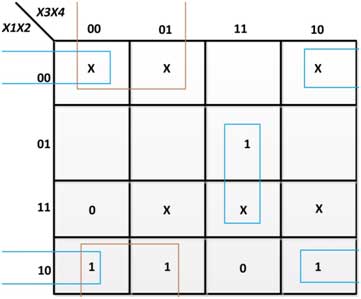
Figure 32 : K-Map for Excess B-3 to BCD Code Converter

Figure 33 : K-Map to C in excess-3 to BCD code converter
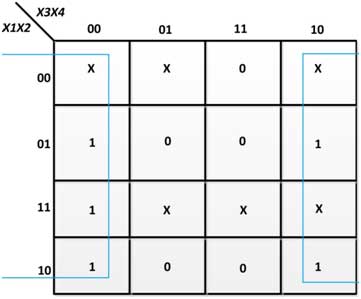
Figure 34 : K-Map to Excess D-3 to BCD Code Converter
From the above K-maps, the following Boolean expressions are obtained for the output variables –
A = X1(X2 + X3.X4)
B = X2  (X3′ + X4′)
(X3′ + X4′)
C = X3  X4
X4
D = X4′
Therefore, the digital circuit for the excess code to BCD converter uses EX-OR, AND, and NOT gates. It can be built using ICs 7486, 7432, 7408 and 7404.
Testing the circuits –
The above designed circuits can be tested by supplying supply voltage to the ICs by a battery through 7805 voltage regulator. The same voltage can be reduced to 2V level using a variable resistor for logic HI while supplying logic LOW through ground . The output signals can be checked by connecting LEDs to the output pins of each converter circuit. Circuits can be verified by checking the truth tables for each circuit.
In the next tutorial, learn how to design a bit magnitude comparator.
Circuit diagrams
| Circuit Diagram-BCD-Excess-3-Converter |  |
| Circuit-Diagram-Excess-BCD Code Converter |  |

