The previous tutorials laid the foundation for logic synthesis and digital circuit design. Digital circuits in general always have application as computing devices, whether as a processor, controller or application-specific ICs. As a computing device, the digital circuit of a processor, controller, or ASIC must essentially be capable of performing arithmetic operations. The implementation of arithmetic operations by digital circuits is further used to construct complex computing logic and mathematical functions.
In a processor/controller/ASIC, arithmetic operations on binary integer numbers are performed by the Arithmetic Logic Unit (ALU), while arithmetic operations on floating point numbers are performed by the Floating Point Unit (FPU). The floating point unit itself is constructed from several ALUs. Within a Central Processing Unit (CPU) or Graphics Processing Unit (GPU) of a computer/computing device, there are many ALUs and/or FPUs (where the FPUs themselves are built from multiple ALUs).
Digital circuits can be of two types – 1) Combinational Logic Circuits or 2) Sequential Logic Circuits. In a combinational circuit, the output of the circuit depends only on the input values at that time. In sequential circuits, the output depends not only on the current input but also on previous output values. ALUs are built using combinational circuits. The ALU is typically designed to perform the following operations:
1) Arithmetic operations – Generally, the arithmetic operations supported by the ALU are addition, addition with carry, subtraction, subtraction with borrowing, two's complement, increment, decrement and pass.
2) Bitwise logical operations – The logical operations supported by the ALU are AND, OR, Exclusive-OR and One's Complement.
3) Bit Shift Operations – Bit shift operations implemented in an ALU include arithmetic shift, logical shift, rotation, and rotation through transport.
Therefore, the ALU can perform arithmetic operations such as addition and subtraction and therefore multiplication and division on binary integers. A binary number may be available to the ALU of a digital processor as an 8-bit, 16-bit, 32-bit, or 64-bit parallel input, depending on whether it is 8-bit, 16-bit, 32-bit, or 64-bit. bit processor. The basic building blocks of the ALU are adders. Adding circuits are built by logic gates and flip-flops. Semiconductor adder circuits can perform addition in a time of less than 1 microsecond.
Let us learn about various combinational circuits – half adder, full adder, half subtractor, full subtractor, N-bit parallel adder, N-bit parallel subtractor, etc., which are generally part of an ALU.
Half Adder –
The half adder is a simple combinational circuit that performs arithmetic addition of two binary digits or addition of two bits. It has two inputs and two outputs. The two inputs are the two 1-bit numbers A and B, while the two outputs are the sum (S) of A and B and the carry (C). The truth table for a half adder is as follows –
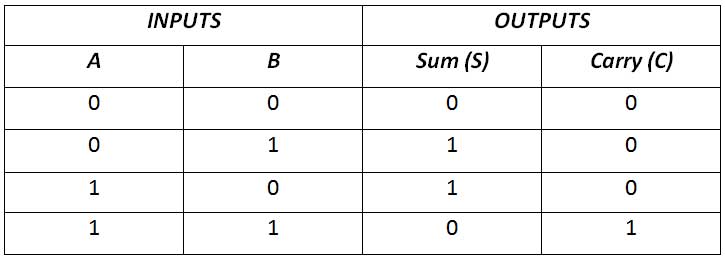
Figure 1: Half Adder Truth Table
From the above truth table it should be clear that the sum is 1 if either of the two inputs is 1, otherwise if both the inputs are 1 or 0 then the sum is 0. This can be implemented by connecting the inputs to a exclusive OR gate. . The carry is 1 only if both inputs are 1, otherwise it is 0. This can be implemented by connecting the inputs to the AND gate. Therefore, the half adder has the following circuit –
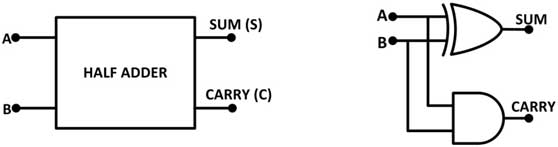
Fig. 2: Symbol and Logic Gate Diagram of the Half Adder
Full adder –
A half adder has only two inputs and there is no possibility of adding a carry from the lower order bits when multiple bit addition is performed. For this purpose full adder is designed. A full adder is designed to perform arithmetic summation of three input bits and produces a summation output and a carry. The truth table for a full adder is as follows –
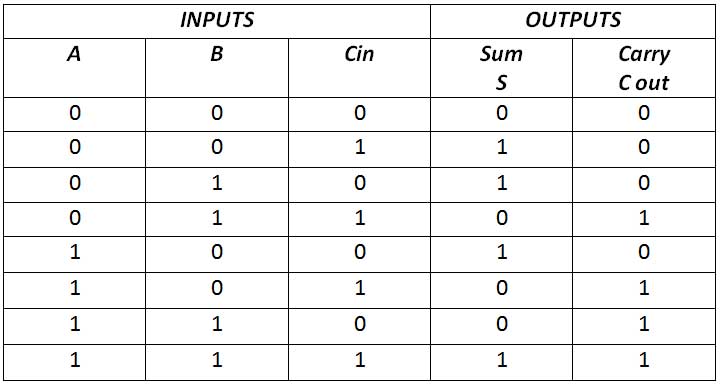
Fig. 3: Full Adder Truth Table
From the truth table, it should be clear that the full adder has three inputs and two outputs. The two input variables are denoted by A and B, which represent the two significant bits to be added. The third entry Cin represents the carry from the previous position of low significance. The outputs are sum (S) and carry (C). From the truth table, it can be seen that the sum is 1 if one of the inputs is 1 or all the inputs are 1. This can be implemented by exclusive OR of all the inputs. The carry is 1 when two inputs are 1 or all inputs are 1. This can be implemented as the sum of the product expression of all inputs. Therefore, the full adder has the following circuit –
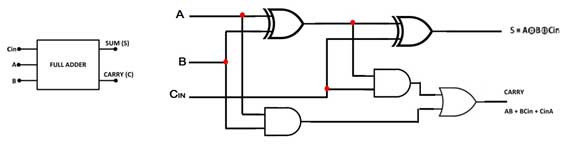
Fig. 4: Full Adder Logic Gate Symbol and Diagram
It can be noted that the full adder is formed by two half-adder circuits and an OR gate.
Half Subtractor –
The half subtractor is a simple combinational circuit designed to perform subtraction of two bits. It has two inputs, X and Y and two outputs Difference (D) and Loan (Bout). The truth table for a half subtractor is as follows –
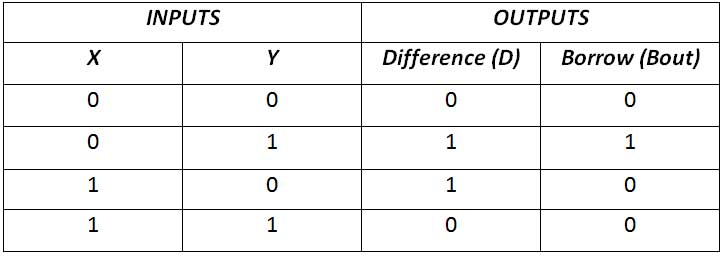
Fig. 5: Half Subtractor Truth Table
From the truth table it can be seen that the difference D is 1 if one of the inputs is 1 otherwise if both the inputs are 1 or 0 the D is 0. This can be implemented by connecting the inputs to a gate exclusive OR. Borrow Out (Bout) is 1 only if Y is 1 but not X. Borrow Out Bout is 1 whenever X is less than Y, so subtraction is done by borrowing 1 from the next higher order bit. This can be implemented by the AND operation between Y and NOT of X. Therefore, the half subtractor has the following circuit –
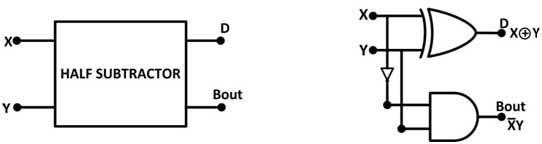
Fig. 6: Symbol and Logic Gate Diagram of the Half Subtractor
Complete Subtractor –
A complete subtractor is designed to perform subtraction involving three bits i.e. minuend bit, subtrahend bit and borrowing from the previous stage. In the full subtractor, it has three inputs X, Y and Bin, and two outputs Difference (D) and Borrow (Bout). There is the following truth table –
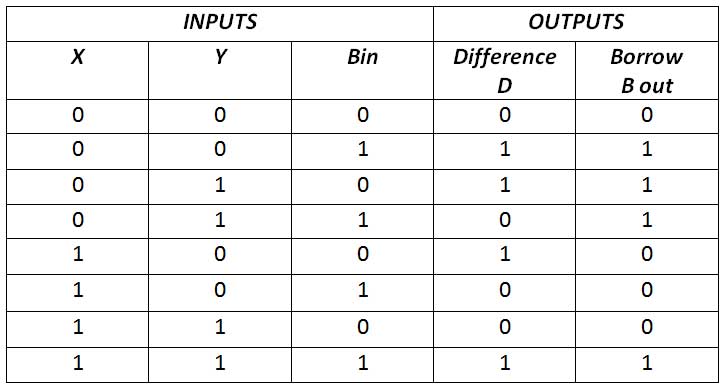
Fig. 7: Complete Subtractor Truth Table
From the truth table, it can be seen that the difference is 1 if one of the inputs is 1 or all inputs are 1. This can be implemented by exclusive OR of all inputs. Borrow Out is 1 if two inputs are 1 or all inputs are 1. This can be implemented as OR operation between two half subtractors. Therefore, the complete subtractor has the following circuit diagram –
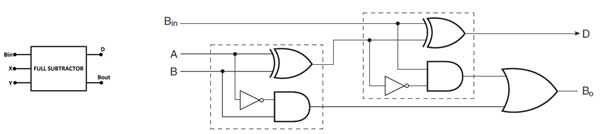
Fig. 8: Symbol and Logic Gate Diagram of the Complete Subtractor
N-bit parallel adder –
Full Adder is capable of adding just two single-digit binary numbers together with a carry input. Practically, it is necessary to add binary numbers that are much longer than just one bit. To add two n-bit binary numbers, you need to use the n-bit parallel adder. It uses multiple cascaded full adders. The transport output of the previous full adder is connected to the transport input of the next full adder.
As a 4-bit parallel adder, it can be constructed by cascading four complete adder circuits. In the circuit A0 and B0 represent the LSB of the four-bit words A and B where Full Adder-0 is the lowest stage. Hence, its Cin has been permanently made 0. The rest of the connections are exactly the same as the n-bit parallel adder. The four-bit parallel adder is a very common logic circuit. A 4-bit parallel adder can be shown by the following block diagram –
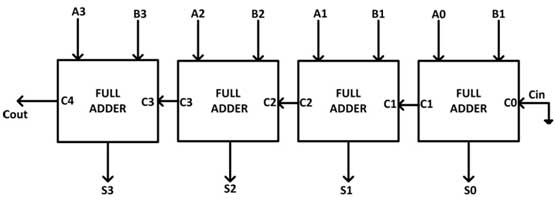
Fig. 9: 4-bit parallel adder logic gate diagram
N-bit parallel subtractor –
Subtraction can be performed by taking the 1 or 2's complement of the number to be subtracted. For example, subtraction (AB) can be performed by adding the 1's or 2's complement of B to A. Therefore, a binary adder can be used to perform binary subtraction. Just as a parallel binary adder can be implemented by cascading multiple full adders, a parallel binary subtractor can also be implemented by cascading multiple full subtractors.
As a 4-bit binary parallel subtractor that subtracts a 4-bit number Y3 Y2 Y1 Y0 from another 4-bit number X3 X2 X1 X0 will have 4 different outputs and borrowed output (Bout). The Bin of the LSB full subtractor is connected to 0 and the Bout of the previous full subtractor is connected to the Bin of the next full subtractor. A 4-bit parallel subtractor can be shown by the following block diagram –
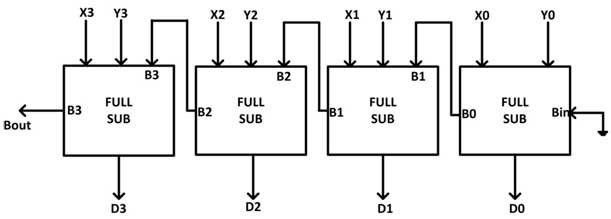
Fig. 10: 4-bit parallel subtractor logic gate diagram
In the next tutorial, learn about gate level minimization and logic gate implementation of the arithmetic circuits discussed above.

