In the previous tutorial, various logic gates and their construction were discussed. In the tutorial – Boolean Logical Operations, it was discussed how, when performing logical operations on binary data, arithmetic operations can be performed. In a digital circuit, many logic gates are interconnected together with registers and memory elements to perform a complex computational task. Any computational problem can be expressed as a Boolean function or Boolean expression.
A Boolean expression takes into consideration the Boolean variables (which can be viewed as individual binary data sources) and represent mathematical relationship (in the form of addition and multiplication) between them. Mathematical operations such as division and subtraction are performed by multiplication and addition themselves. Similarly, subtraction can be implemented by addition with the complement and division can be implemented by multiplying the divisor by a factor and subtracting.
Boolean functions or expressions follow a set of mathematical rules that are collectively called Boolean algebra. The various theorems of Boolean algebra are useful for minimizing a Boolean function. To design an optimized digital circuit (minimum number of logic gates to solve a specific computational problem), a Boolean expression must be minimized. So, let's start with basic theorems and postulates of Boolean algebra.
Huntington's postulates –
Boolean Algebra was developed by George Boole in the year 1854. In 1904, EV Huntington formulated several postulates that must be satisfied by a Boolean algebraic system. These postulates are as follows –
1) Closure – If a Boolean expression involves certain variables that belong to a set say S, then the set S is closed with respect to a binary operator if for each pair of elements of S, the binary operator specifies rules for obtaining an element unique to S. In other words, if a Boolean function involves certain Boolean variables, then the variables as well as the result of the Boolean expression must belong to a common set of elements. Any Boolean expression always follows closure with respect to binary addition (+ operator) and binary multiplication (. operator).
2) Identity – A set is said to have an identity element for an operator (like *) if there exists an element, say e in the set, such that e belongs to the set and multiplication of e with any other element results in the same element, that is, if x also belongs to the same defined, then x*e = e*x = x. In a Boolean system, the identity element with respect to binary addition is 0, as for any Boolean variable, say x, x + 0 = 0 + x = x. Similarly, the identity element in relation to binary multiplication is 1, as for any Boolean variable, say x, x.1 = 1.x = x.
3) Commutative – Any Boolean expression is commutative with respect to binary addition as well as binary multiplication. As if there are two Boolean variables – x and u , then x + y = y + x. Likewise, xy = yx
4) Associative – Any Boolean expression is also associative with respect to binary addition as well as binary multiplication. As if there are three Boolean variables – x, y and z, then x + (y + z) = (x + y) + z. Likewise, x.(yz) = (xy).z.
5) Distributive – In Boolean algebra, binary addition is distributive over binary multiplication and binary multiplication is distributive over binary addition. So, if there are three Boolean variables – x, y and z, then x.(y + z) = (xy) + (xz). Likewise, x+(yz) = (x+y). (x+z).
6) Inverse – Boolean algebra does not have an additive or multiplicative inverse, as there are no subtraction and division operations in Boolean algebra. However, any Boolean element, say x, has a complement x' such that x + x' = 1 and xx' = 0.
The associative law is not a postulate of Huntington, but it is valid for Boolean algebra. It should also be noted that Boolean algebra has + over distributive operator. operator. This is different from the laws of ordinary algebra. It is also important to note that Boolean algebra has a complement, but not an inverse. The Boolean algebra used in digital electronics is a two-valued Boolean algebra. It is defined over a set, say B, which has only two elements – (0, 1). All the postulates mentioned above are valid in two-valued Boolean algebra as follows –
1) Closure – The result of any Boolean expression is 0 or 1. Therefore, it follows the closure law in relation to the set (0, 1).
2) Identity – The 0 is the identity element in relation to binary addition, as for any Boolean variable, say x, 0 + x = x + 0 = x. If x = 0, then 0 + 0 = 0 + 0 = 0. If x is 1, then 0 + 1 = 1 + 0 = 1. The 1 is the identity element in relation to binary multiplication as for any Boolean variable, let's say x, 1.x = x.1 = x. if x = 0, then 1.0 = 0.1 = 0. if x = 1, then 1.1 = 1.1 = 1.
3) Inverse – 0's complement is 1 and 1's complement is 0. In binary addition, 0 + 1 = 1 and in binary multiplication, 0.1 = 0. For any Boolean variable say x, x + x' = 1 and xx' = 0.
Principle of Duality –
Duality is an important property of Boolean algebra. According to this property, any Boolean expression, deducible by the postulates of Boolean algebra (Huntington's postulates together with the associative property), remains the same if the operator and identity elements are swapped. Therefore, the dual of a Boolean expression can be obtained by interchanging the AND and OR operators and replacing all 1s with 0s and 0s with 1s.
Boolean Theorems –
Any Boolean expression is deducible by the following theorems –
Theorem 1 – For any Boolean variable x, x + x = x and xx = x. Suppose, if x = 0, then 0 + 0 = 0 and 0.0 = 0. If x = 1, then 1 + 1 = 1 and 1.1 = 1.
Theorem 2 – For any Boolean variable x, x + 1 = 1 and x,0 = 0. Suppose, if x = 0, then 0 + 1 = 1 and 0.0 = 0. If x = 1, then 1 + 1 = 1 and 1.0 = 0.
Theorem 3 (Involution) – For any Boolean variable x, (x')' = x. Suppose x = 0, then (0′)' = 1′ = 0. If x = 1, then (1′)' = 0′ = 1.
Theorem 4 (associative) – For any Boolean variables x, y and z, x + (y + z) = (x + y) + z and x. (y. z) = (x. y) . z.
Theorem 5 (DeMorgan's Theorem) – This theorem establishes the law of duality for Boolean algebra. For any Boolean variables x and y, (x + y)' = x' . y' and (xy)' = x' + y'.
Theorem 6 (Absorption) – For any Boolean variables x and y, x + (x. y) = x and x. (x + y) = x. This can be proved as follows –
x + (x. y) = (x. 1) + (x. y)
=x(1+y)
=x. 1
=x
Similarly,
x. (x + y) = (xx) + (xy)
=x + (x.y)
= (x. 1) + (x. y)
=x(1+y)
=x. 1
=x
Operator precedence in Boolean algebra –
The operator precedence in descending order in Boolean algebra is as follows – 1) Parentheses, 2) NOT, 3) AND and 4) OR. Any Boolean expression is deduced from left to right and the highest precedence is in parentheses. Then NOT, AND and finally OR operator.
Boolean Function –
A Boolean function is a Boolean algebraic expression that consists of Boolean variables (where each variable can have a value of 0 or 1), Boolean constants (i.e. 0 and 1), and Boolean operators (such as AND, OR, NOT). Any Boolean function practically represents some calculation on binary data. For example, let a Boolean function say F to be like –
F = x + yz
Here x, y and z are boolean variables (binary data sources like binary cells of a record) which are related by AND and OR operators in the above function. All possible results of a Boolean expression can be represented by a truth table. The truth table lists all possible combinations of the Boolean variable values and compares with the result of the Boolean expression. As for the above stated function, the following is the truth table –
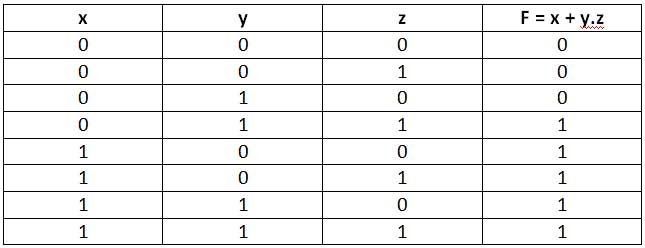
Figure 1: Truth table for a Boolean function
A digital circuit for the above Boolean function is nothing more than the interconnection of logic gates (AND, OR, NOT) with binary data sources (represented by Boolean variables in the Boolean function). Binary multiplication or dot operation between two variables is equivalent to connecting two binary sources as input of AND gate. Binary addition or addition operation between two variables is equivalent to connecting two binary sources as input of OR gate. The complement is equivalent to connecting a binary source to a NOT gate. Therefore, the digital circuit for the above function will be as follows –
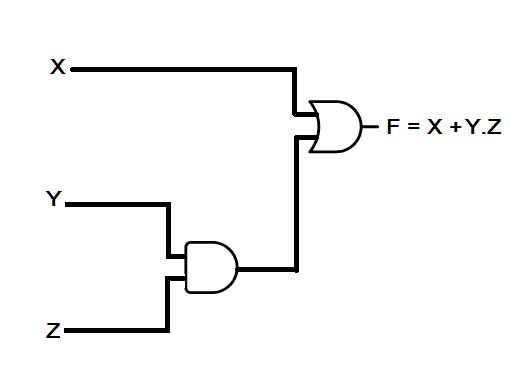
Fig. 2: Image showing Boolean Function converted into Logic Circuit
Complement of a Boolean function –
The complement of a Boolean function is obtained by changing all 0s to 1s and 1s to 0s and swapping the AND and OR operators. In a Boolean function, replacing all 0s with 1s and all 1s with 0s is done by replacing Boolean variables with their complements. For example, the complement of the function given above will be as follows –
If F = x + yz, then
F' = x' . (y' + z')
Minterm and Maxterm –
A Boolean variable can output in its normal form (as x) or in its complementary form (as x') in a Boolean expression. If the AND operation is done between two variables, say x and u , there can be four possible combinations – xy, x.y', x'.y and x'.y'. Each of these possible products are called Minterm or standard product. Similarly, if the OR operation is done between two variables, say x and u , then again there are four possible combinations – x + y, x + y', x' + y, and x' + y'. Each of these possible sums are called Maxterm or standard sums.
For two variables, x and y, the following Minterms and Maxterms are possible –
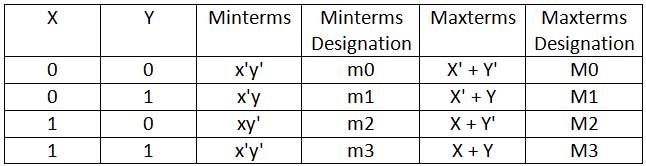
Fig. 3: Table listing Minterms and Maxterms for two Boolean variables
Similarly, for three variables, say x, y and z, the following Minterms and Maxterms are possible –
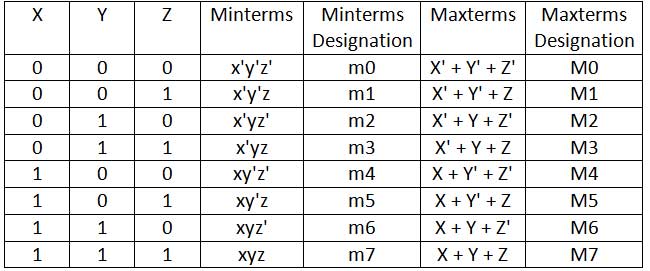
Fig. 4: Table listing Minterms and Maxterms for three Boolean variables
For n variables, there can be 2^n Minterms and 2^n Maxterms. Any Boolean function can be expressed as the sum of Minterms producing 1 for the function in the truth table or Product of Maxterms producing 0 for the function in the truth table, as long as the truth table for the function is known. For example, there is a function F, with the following truth table – Similarly, for three variables, say x, y and z, the following Minterms and Maxterms are possible –
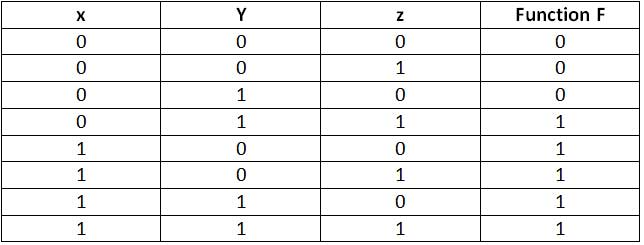
Fig. 5: Truth table for a three-variable Boolean function
From the truth table above, the function F can be expressed as the sum of the minterms yielding 1 for the function in the truth table as follows –
F = x'yz + xy 'z' + xy'z + xyz ' + xyz = m3 + m4 + m5 + m6 + m7 From the truth table above, the function F can be expressed as the sum of the Minterms yielding 1 for the function in the truth table as follows –
Similarly, it can be expressed as product of Maxterms yielding 0 for the function in the truth table as follows –
F = (x' + y' + z') . (x' + y' + z) . (x' + y + z') = M0 . M1. M2
A function expressed as sum of minterms or product of maxterms is said to be in its canonical form. As for n number of variables, there can be 2^n minterms and 2^n maxterms, the number of possible functions with n number of variables is 2^2n. So for 2 Boolean variables there can be 4 minterms and 4 maxterms and the total number of functions possible with them is 16. So there can be 16 binary functions (binary operations) possible between two Boolean variables or (binary sources ).
When expressing a function in the form of Minterms and Maxterms, it can have two-level implementation in logic gates. Two-level implementation is always preferred, as it produces the least amount of delay across the gates when signal propagates from the input to the output of the digital circuit.
In the next tutorial, learn about all the possible logical operations between two Boolean variables. There are additional logical operations besides AND, OR, and NOT. All possible logical operations between two binary sources can be derived with knowledge of Boolean functions and theorems.

