Modulus of elasticity
Definition
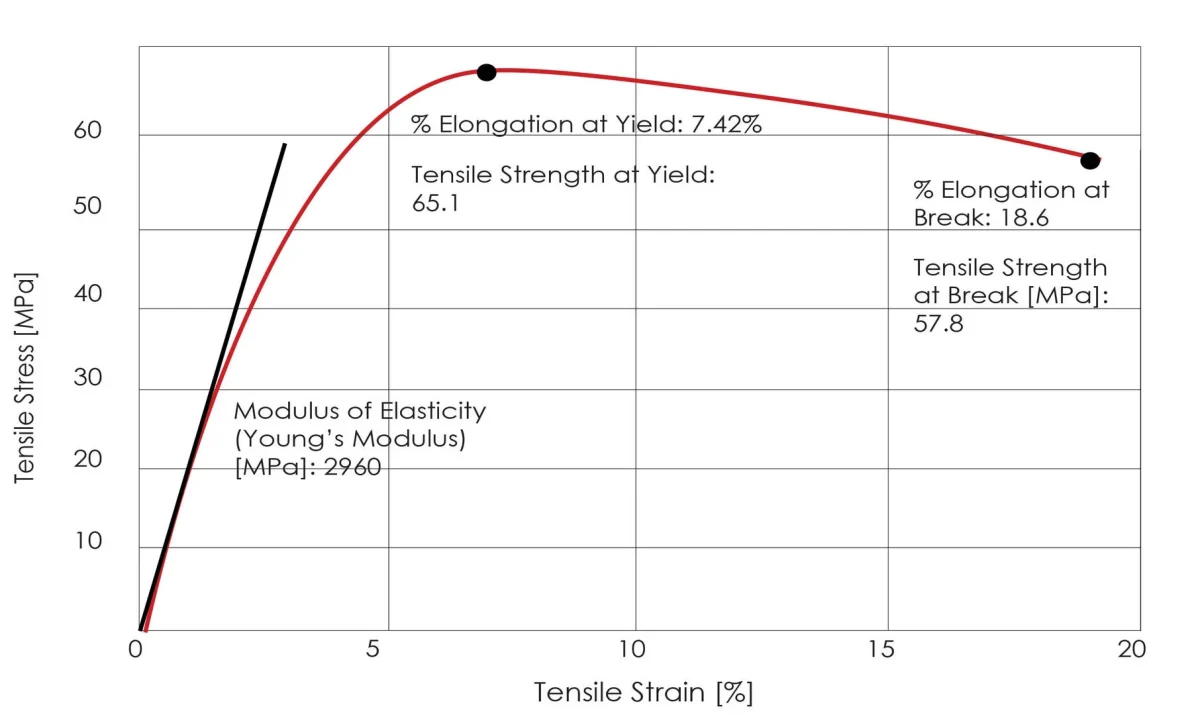
Modulus of elasticity: The relationship between the normal stress and the corresponding normal strain in the elastic deformation stage of a material.
In the elastic deformation phase, the stress and strain of a material are proportional, according to Hooke's Law, and the proportionality coefficient is referred to as the modulus of elasticity.
The term “modulus of elasticity” is a general description of the elasticity of a material. It covers several specific moduli, including Young's modulus, shear modulus, and volume modulus, among others.

1. Rigidity
Stiffness” refers to the ability of a structure or component to resist elastic deformation. It is determined by the force or moment required to produce one unit of deformation.
In terms of rotational stiffness, it is represented by “k” and can be calculated as “k = M/θ”, where “M” is the applied torque and “θ” is the angle of rotation.
Other stiffnesses include:
- tension and compression stiffness
- axial force ratio axial linear strain (EA)
- shear stiffness
- shear force ratio to shear deformation (GA)
- torsional rigidity
- torsional deformation torque ratio (GI)
- bending stiffness
- curvature of the bending moment (EI) ratio.
2. Calculation method
The stiffness calculation method can be divided into two approaches: the theory of small displacements and the theory of large displacements.
Large displacement theory takes into account the deformation of the structure after stress and forms the equilibrium equation accordingly, providing accurate results but with a more complex calculation process.
In contrast, small displacement theory assumes that the structure is not significantly deformed, so the internal force can be obtained from the external load and then used to calculate the deformation.
This approach is widely used in most mechanical design applications as it is much simpler to solve.
For example, in calculating the bending deformation of the beam, the small displacement theory is often employed because the actual deformation is very small.
This theory involves ignoring the first derivative of deflection in the curvature formula and using the second derivative of deflection to approximate the curvature of the beam axis, which helps simplify the solution process by linearizing the differential equation.
When multiple loads act simultaneously, the bending deformation caused by each load can be calculated separately and then combined.
3. Classification and meaning
Resistance to deformation under a static load is known as static stiffness, while resistance to deformation under a dynamic load is referred to as dynamic stiffness, that is, the amount of dynamic force required for unit amplitude.
When the interfering force changes slowly (that is, the frequency of the interfering force is much lower than the natural frequency of the structure), the dynamic stiffness is essentially the same as the static stiffness.
However, if the interfering force changes rapidly (that is, the frequency of the interfering force is much greater than the natural frequency of the structure), the structural deformation will be relatively small and therefore the dynamic stiffness will be relatively large.
If the frequency of the interfering force is close to the natural frequency of the structure, resonance occurs, and the dynamic stiffness will be minimal, making the structure the easiest to deform, with its dynamic deformation capable of reaching several times or even more than ten times greater than the deformation of static load.
Excessive deformation of components may affect their functioning.
For example, excessive deformation of a gear shaft can affect gear engagement, and excessive deformation of a machine tool can reduce machining accuracy.
Factors that affect stiffness include the materials' modulus of elasticity and structural form. Changing the structural shape can have a significant impact on stiffness.
Stiffness calculation is the basis of vibration theory and structural stability analysis. When the mass remains constant, the high stiffness results in a high natural frequency.
The stress distribution in a statically indeterminate structure is related to the stiffness index of each part.
In fracture mechanics analysis, the stress intensity factor of a cracked member can be determined based on its flexibility.
III. Stiffness vs Elastic Modulus
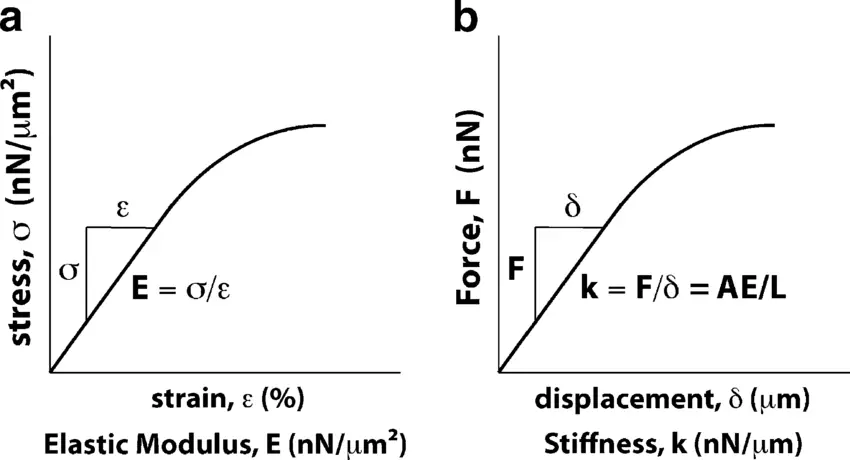
In general, stiffness and modulus of elasticity are different concepts.
Stiffness and modulus of elasticity are measures of a material's resistance to deformation. Stiffness is a general term for the resistance to change when a force is applied, while modulus of elasticity, also known as Young's modulus, is a specific measure of the amount of deformation resulting from applied stress. Both are fundamental in materials science, but differ in application and units of measurement.
The modulus of elasticity is a property of material components, while stiffness is a property of solids.
In other words, modulus of elasticity refers to the microscopic property of a material, while stiffness refers to the macroscopic property of a material.
In materials mechanics, the product of the modulus of elasticity and the moment of inertia of the cross-section of a beam is expressed as various stiffnesses.
For example, “GI” represents torsional stiffness and “EI” represents flexural stiffness.
1. Rigidity
Stiffness refers to a part's resistance to elastic deformation under load.
The stiffness of a part is typically expressed as the force or moment required for a unit deformation.
This property is determined both by the material's modulus of elasticity and its geometry.
In the case of isotropic materials, the stiffness also depends on their shear modulus (according to Hooke's law).
External forces and other factors, such as boundary conditions and geometry, also play a role in determining the stiffness of a structure.
In engineering design, analyzing the stiffness of materials and structures is crucial, especially for parts sensitive to elastic deformation such as spindles, guide rails and lead screws.
Stiffness analysis is also critical for structures that require rigorous control of deformation, such as wings and high-precision assemblies.
It is important for many structures, such as buildings and machines, to control stiffness to prevent vibration, chatter and instability.
Devices such as spring scales and ring dynamometers also require control of their stiffness to function properly.
In structural mechanics displacement analysis, the stiffness of each part must be analyzed to determine its deformation and stress.
2. Intensity
The ability of metallic materials to resist permanent deformation and fracture under the action of external forces is known as strength.
It mainly includes yield strength, tensile strength, compressive strength, flexural strength, among others.
Yield strength and tensile strength are often used in engineering, and these two strength indices can be determined through a tensile test.
Strength is a crucial index for measuring the load-bearing capacity of parts and their ability to resist failure, and is a fundamental requirement for mechanical parts.
The strength of mechanical parts can typically be divided into static strength, fatigue strength (bending fatigue and contact fatigue), fracture strength, impact strength, high and low temperature strength, strength under corrosive conditions, bond strength, and other factors.
The study of strength is a comprehensive examination, mainly focusing on the stress state of parts and components and predicting the conditions and timing of failure through the stress state.
Strength refers to the ability of materials to withstand external forces without being damaged, which also includes irrecoverable deformations.
It can be categorized into the following types based on the types of forces:
- Compressive strength – the ability of a material to withstand pressure;
- Tensile strength — the ability of a material to resist tensile force;
- Flexural strength — the material's ability to withstand external bending force;
- Shear strength – the ability of a material to resist shear force.