Residual stress is a type of internal stress referred to as such in engineering. The distribution of residual stress in a part is often uneven, which can significantly impact its static strength, fatigue strength, shape stability and corrosion resistance. As a result, measuring residual stress is crucial.
There are two main methods for measuring residual stress: destructive testing and non-destructive testing. The destructive testing method involves removing a portion of the part and calculating the residual stress based on the corresponding deformation and displacement. Common destructive testing methods include the drilling method and the ring core method.
The non-destructive testing method involves establishing a relationship between the residual stress and a physical quantity that can cause a change in the material (such as crystal plane spacing, ultrasonic wave propagation rate, or magnetic permeability) to calculate the residual stress. Non-destructive testing methods include X-ray diffraction, neutron diffraction, magnetic and ultrasonic methods.
X-ray diffraction is the most widely used method for measuring residual stress, due to its mature principles and well-established methods, as well as the availability of increasingly sophisticated test equipment, including laboratory instruments, portable instruments for measuring field and specialized devices. for special circumstances.
The X-ray diffraction method for measuring residual stress was first proposed by Russian scholar Akchenov in 1929 and equated macroscopic strain with lattice strain. In 1961, German scholar Macherauch further developed the sin 2 ψ method based on Akchenov's idea, making measurement of residual stress by X-ray diffraction a reliable and widely used technology.
Over the past 60 years, X-ray diffraction has developed into several different measurement methods, with sin 2 ψ method and cosα method being the two main methods used today.
1. Classification of residual stress measurement methods by X-ray diffraction
To master X-ray diffraction technology for measuring residual stress, it is important to understand its various methods.
(1) X-ray diffraction residual stress measurement methods can be categorized into two main approaches: the sin 2 ψ method and cosα method.
(2) Sin 2 The ψ method can further be classified based on the residual stress calculation method, the 2θ method, the value method and the strain method.
(3) Based on the geometric relationship between ψ and 2θ, the sin 2 The ψ method can be divided into two types: the co-tilt method and the roll method.
(4) The measurement method can also be differentiated based on the scanning mode of the X-ray tube and the counter tube, the fixed ψ0 method and the fixed ψ method.
(5) Within the roll method, there are three subcategories: the standard roll method, the modified roll method, and the ψ-roll clamping method.
(6) The positive and negative ψ measurement method is used to determine the shear stress τφ.
(7) X-ray diffraction is typically used to measure stress in a specific direction at a specific point, but there are also methods for measuring principal stress at a point.
(8) The oscillation method can be divided into several subcategories: the ψ0 oscillation method, the ψ oscillation method, the Debye ring oscillation method, the φ angle oscillation method and the X/Y reciprocal translation method .
(9) In terms of diffraction geometry, there are three approaches: the focusing method, the quasi-focusing method, and the parallel beam method.
2. sin 2 ψ method for determining residual stress by X-ray diffraction
Stress is determined by strain. In the case of polycrystalline materials, the residual stress is estimated by the statistical result of the lattice deformation in the relevant region.
Thus, the residual stress can be determined by measuring the lattice deformation using the X-ray diffraction technique.
The residual stress of the material reflects the macro deformation.
Macro deformation is equivalent to lattice deformation.
Lattice strain represents the relative change in crystal plane spacing, which can be calculated using a diffraction device based on Bragg's law.
This summarizes the X-ray diffraction method for measuring residual stress.
2.1 Bragg's Law
When a polycrystal is exposed to an X-ray beam of specific wavelength (λ), the maximum intensity of the reflected X-ray (i.e., the diffraction peak) will be observed at a specific diffraction angle (2θ), as illustrated in Figure 1. This phenomenon is known as X-ray diffraction.
The relationship between the X-ray wavelength (λ), the crystal plane spacing (d) and the Bragg angle (θ) is described by the following equation (1).
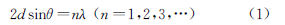
In X-ray diffraction analysis of residual stress, the appropriate target material for the X-ray tube is selected to determine the suitable wavelength (λ). The diffraction angle (2θ) is then measured using a diffraction device. Based on the measurement, the crystal plane spacing (d) of the relevant crystal plane can be calculated.
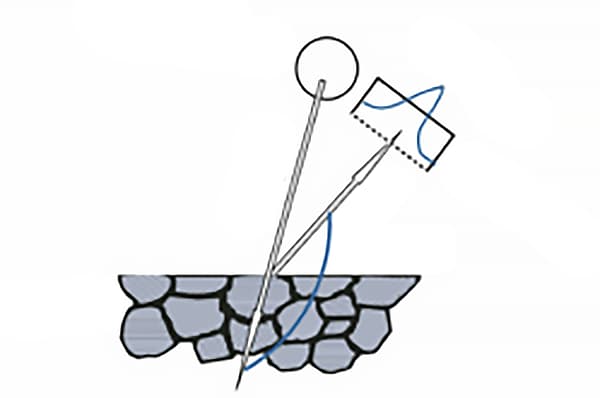
Fig. 1 X-ray diffraction geometry
2.2 Azimuthal angle of diffraction of the crystalline plane ψ
According to the law of reflection in optics, the normal of the crystal plane involved in diffraction must be at the bisector between the incident and reflected rays, as illustrated in Figure 2.
The angle between the normal of the diffraction crystal plane and the normal of the sample surface is known as the azimuthal angle of the normal of the diffraction crystal plane, which is generally represented by ψ.
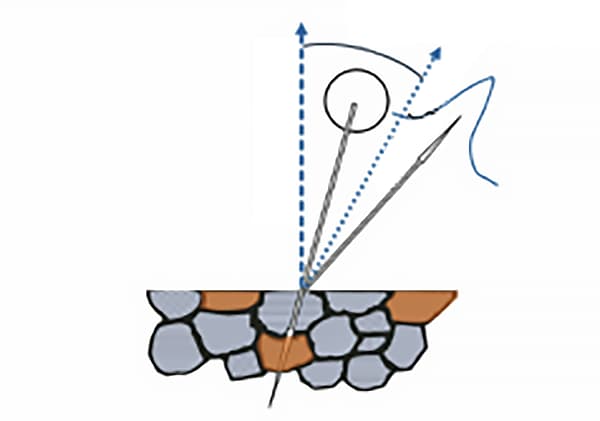
Fig. 2 Schematic diagram of the crystalline X-ray diffraction plane Azimuth ψ
Bragg's law allows the determination of the spacing (dψ) of crystalline planes in a specific orientation (ψ).
If the spacing (d0) of the crystal planes in the stress-free state is known, the lattice strain (εψ) in the designated orientation can be calculated.
2.3 Scope of application of sin 2 ψ d method
S1, S2 and S3 are the axes of the sample surface and S1 is defined by the researcher.
Figure 3 illustrates the coordinate system used to measure residual stress using X-ray diffraction.
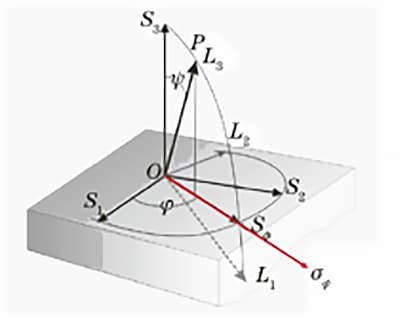
Fig. 3 Coordinate system for measuring X-ray diffraction stress
According to generalized Hooke's law, the deformations of these crystalline planes are influenced by the stress tensor at point O and are closely linked to the sine and cosine of φ and ψ, the material's Young's modulus and Poisson's ratio.
Thus, it is possible to determine the three-dimensional stress at point O, including the stress (σφ).
The expression for strain in the OP direction can be derived from the theory of elasticity.
For most materials and components, the penetration depth of X-rays is only a few microns to tens of microns, therefore it is commonly assumed that σ 33 =0.
Therefore, the deformation in the OP direction is represented by equation (2).
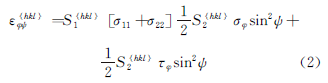
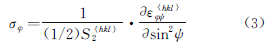
Sin 2 The ψ method formula is derived based on Bragg's law and elastic theory.
The objects considered in the theory of elasticity are considered homogeneous, continuous and isotropic media.
However, this assumption is only valid for polycrystalline metallic materials if the grain size is fine and there is no texture present.
Figure 4 shows the functional relationship curve of ε n and sin 2 ψ for isotropic materials, materials with a stress gradient or composition gradient, materials with shear stress and anisotropic materials with texture.

As shown in Fig. 4c), if the shear stress τ 13 ≠ 0, τ 23 ≠0 and sin 2 The curve ψ has bifurcation ± ψ, σ φ and τ φ can be obtained using the measured strain data ε ﹢ψ and ε ﹣ψ in a series of angles ± ψ, as shown in Formula (4) and Formula (5).
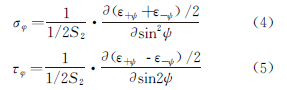
It is important to note that sin 2 The ψ curve shown in Figure 4c) is unlikely to have a ±ψ bifurcation.
This is because the X-ray used for diffraction has limited penetration depth into the material being tested, generally from just a few microns to tens of microns.
Consequently, the stress components perpendicular to the surface of the material can be considered zero.
Only when the main stress plane deviates from the sample surface under the condition of special machining (such as powerful grinding and large cutting amount) can τ 13 ≠0 and τ 23 ≠0 occur.
The ±ψ bifurcation is not a common occurrence and the fitting curve generally does not have the ellipse attribute. This is largely due to systematic error in the ±ψ mechanism of the goniometer. Therefore, there is no need to overemphasize the importance of ellipse fitting.
In conclusion, the practical and implementable process of determining residual stress through X-ray diffraction involves selecting a few angles ψ (or several pairs of angles ±ψ) and measuring the corresponding diffraction angle (2θφψ), followed by calculating .
Scholars have developed various methods for organizing the spatial geometric relationship between the ψ plane and the 2θ plane, determining the diffraction curve and performing calculations.
3. True strain method, 2θ method and d-value method
The diffraction angle 2θ φψ is measured by the X-ray diffraction device, and the corresponding crystal plane spacing is calculated as d φψ according to Bragg's law, then the lattice deformation ε φψ can be expressed by the lattice spacing crystal plane, as shown in Formula (6).
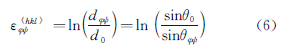
The true strain is directly substituted into Equation (3), Equation (4) and Equation (5) to calculate the stress, which is the expression of the true strain method.
The true strain method is adopted and the exact values of d 0 and θ 0 are not required.
In most cases, the true strain method has significant advantages.
Approximate equations can also be used to calculate the strain, as shown in Eq. (7) and Eq. (8).
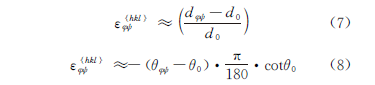
The calculation formula of the 2θ method is shown in equation (9).
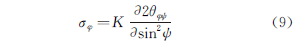
Where, K is the voltage constant, and its calculation formula is shown in equation (10).
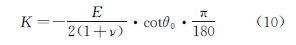
Where: ν is the Poisson’s ratio of the material.
For some materials, θ 0 varies greatly with chemical composition, and results will deviate greatly if the stress constant is used.
The true strain method has been included in the European Union standard EN 15305-2008 Non-destructive testing – Test method for residual stress analysis by X-ray diffraction and GB/T 7704-2017 X-ray stress measurement method for testing non-destructive.
The XL-640 household strain gauge lists the true strain method as the default strain calculation method, and the 2θ method can be selected for calculation.
4. Co-tilt method and roller method
The coplanar method is a measurement method in which the 2θ plane coincides with the ψ plane (stress direction plane), as shown in Figure 5.
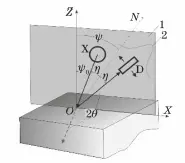
Fig. 5 Geometric diagram of the same slope method
With the same tilt method, the X-ray incidence angle ψ 0 is dominant, while the angle ψ can be calculated, as shown in Eq. (11) and Eq. (12).
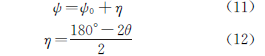
In the tension test of the actual part, when the test point is located in a similar shallow groove, the test space of the goniometer is limited, so the same tilt method is more suitable.
The roll method is a measurement method in which the 2θ plane and the ψ plane (stress direction plane) are perpendicular to each other, as shown in Fig.
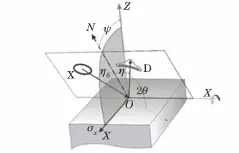
Fig. 6 Geometric Diagram of the Roll Method
The main characteristic of the Roll method (χ method) is its small diffraction peak absorption factor, which contributes to increasing measurement accuracy.
The 2θ and ψ ranges can be fully extended as needed. For certain materials, diffractive rays with low peak positions (such as peaks below 145°) can be used for strain measurement.
However, the 2θ plane and ψ plane of this method are perpendicular to each other, requiring a three-dimensional space, making it challenging to apply in measuring narrow spaces.
A foreign company's voltage instrument product employs a modified Roll method with dual detectors, as shown in Figure 7. Its geometric layout is shown in the figure.
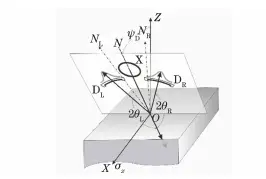
Fig. 7 Geometric diagram of the modified roller method
As early as January 1977, Li Jiabao, Institute of Metals, Chinese Academy of Sciences, proposed this test method and calculation formula, as shown in Eq. (13) and Eq. (14).
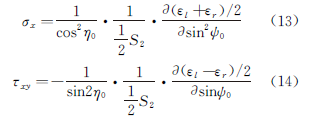
The roll method can be divided into two categories: the fixed ψ0 method and the fixed ψ method.
The fixed ψ method is considered superior to the fixed ψ0 method due to its more precise principles and effective results in practice.
By combining these two methods, the fixed roll method ψ, the absorption factor can be equal to 1.
This means that the diffraction peak will not tilt at the bottom back, the shape of the peak will remain symmetrical, and the shape and intensity of the peak will remain unchanged even if the angle ψ changes, as long as there is no texture.
This feature greatly increases measurement accuracy, making the roller-fixed ψ method an ideal measurement technique.
5. Balance method
The oscillation method involves using each defined angle ψ (or angle ψ0) as the center point and making the X-ray tube and detector swing left and right at a specific angle (±Δψ or ±Δψ0).
This method increases the number of grains that participate in diffraction, making it an effective method for measuring stress in coarse-grained materials.
Other oscillation methods such as the φ angle oscillation method and the X/Y translation oscillation method can also be used, and different oscillation methods can even be combined for testing purposes.
6. Determination of residual stress by X-ray diffraction cosα method
In 2012, PULSTEC, a company based in Japan, first introduced a tension instrument that uses two-dimensional sensing technology.
This instrument operates using a single incident mode and a two-dimensional detector to collect X-ray diffraction information, allowing you to quickly collect Debye ring data at the test point.
Since the angle ψ formed by the crystal face normal and the sample surface normal is not in the same plane for each point of the Debye ring, the sin 2 The ψ method cannot be used to calculate the stress. Instead, the angle α, or cosα, method is employed (as shown in Figure 8).
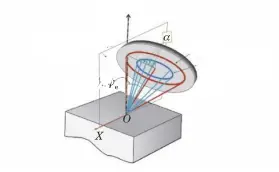
Fig. 8 Geometric Diagram of the cosα Method
This test method is ideal for measuring surface tensions in large steel structures.
However, it has limitations when testing coarse-grained materials or textured materials.
The cosα method is based on the principles of elasticity, as demonstrated by Equations (15) and (16).
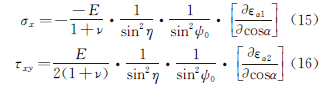
Figure 9 shows the maximum angle range ψ that can be acquired using a “full two-position detector” (with an incident angle of 45°).
The angle α is in the plane of the Debye ring, which is the central angle of each point in the Debye ring.
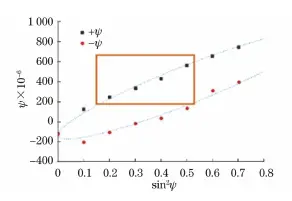
Fig. 9 Location of sin 2 ψ method data points on the s curve
Both methods for measuring residual stress through X-ray diffraction are based on the same mechanical principle.
The strain tensor can be transformed into the spatial angle, and the angle α used in the cosα method can be fully converted into the angle ψ.
In essence, the cosα method is essentially an approximation of the sin 2 ψ method.
7. Comparison of residual stress of hot rolled steel sheet measured by different instruments
Typically, hot-rolled steel plates are considered to be texture-free. However, some parts of the steel plate may have texture due to various factors.
Despite this, many users still choose to use X-ray diffraction to measure residual stress in these cases.
For example, if a textured hot-rolled steel plate is selected, the test conditions and results can be seen in Table 1 and Table 2. The test report for measuring residual stress at point Z (0) for each instrument is shown in Figures 10-13.
Table 1 Test parameters for measuring residual stress of hot-rolled steel sheet with different stress instruments
| Kind of equipment | μ-X360S | PROTOLXRD | X-RAY | XL-640 |
| test method | cosα | sin 2 ψ | sin 2 ψ | sin 2 ψ |
| Voltage/kV | 20 | 30 | 20 | 25 |
| Current/mA | 1 | 25 | 1 | 6 |
| Illuminated point/mm | 1 | 1 | 1 | 1 |
| ψ Range/(°) | – | -35~35 | -40~40 | 0~45 |
| Deformation calculation method | – | D-value method | Tension method | Tension method |
| Peak determination method | – | PersonVII | Midpoint | Cross-correlation method |
| Residual stress/MPa | 78 | 213.6 | 144 | 113 |
Table 2 Residual stress of hot-rolled steel sheet measured by different stress instruments
| Test point | μ-X360S | PROTOLXRD | X-RAY | XL-640 |
| Z(5) | 29.47 | 122 | 107 | 77 |
| Z(4) | 37.52 | 135 | 112 | 70 |
| Z(3) | 74.70 | 104 | 95 | 67 |
| Z(2) | 38.28 | 153 | 99 | 134 |
| Z(1) | 37.64 | 166 | 122 | 101 |
| Z(0) | 64.78 | 144 | 213 | 113 |
| Z(-1) | 72.71 | 138 | 97 | 139 |
| Z(-2) | 62.52 | 134 | 83 | 145 |
| Z(-3) | 75.70 | 120 | 93 | 153 |
| Z(-4) | 63.56 | 114 | 80 | 148 |
| Z(-5) | 79.27 | 94 | 93 | 152 |
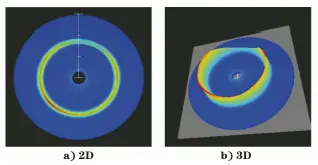
Fig. 10 Debye ring at point Z (0) measured with a μ-X360S strain gauge
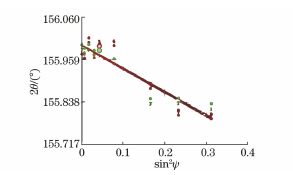
Fig. 11 2θ-sin 2 ψ curve of Z (0) measured by PROTO LXRD strain gauge
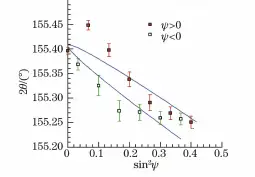
Fig. 12 2θ-sin 2 ψ Curve of measuring point Z (0) with X-RAYBOT strain gauge
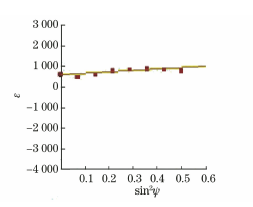
Fig. 13 ε-sin 2 ψ curve of Z (0) measured with XL-640 strain gauge
The residual stress measured by method c is smaller than that measured by method s.
For the Z (0) test point, the voltage meter is used. According to the principle of equal sin 2ψ spacing, 8 angles ψ are selected within the range of 0°~45°.
The results are shown in Figure 14-15. It can be seen that sin 2 The ψ curve of the material presents a “shock” type due to the texture.
The ordinate of sin 2 The curve ψ in Fig. 13 is the strain ε. After changing the ordinate to 2θ, perform the linear fit. The results are shown in Figure 14.
The slope M of the fit line is -0.355 and the residual stress σ is 113MPa.
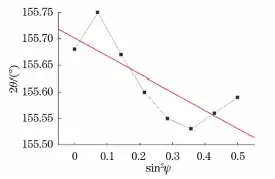
Fig. 14 Fitting results of 2θ-sin 2 ψ curve measured by XL-640 strain gauge at point Z (0)
The ψ range selected by the μ-X360S strain meter is equivalent to the first two shielding 2θ values, and then straight-line adjustment is performed. The results are shown in Figure 15.
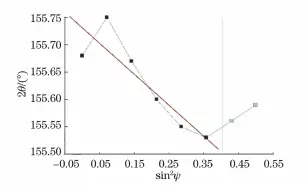
Fig. 15 Fitting results of 2θ-sin 2 ψ Z curve (0) measured by voltage instrument type μ-X360S
Use the PROTO LXRD strain gauge to test the selected ψ range, secure the last three 2θ values in Fig. 14, and then perform linear adjustment. The results are shown in Fig.16.
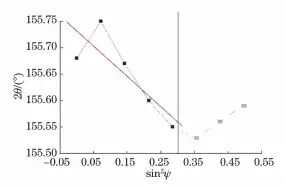
Fig. 16 Fitting results of 2θ-sin 2 ψ curve measured by PROTO LXRD strain gauge at point Z (0)
It can be seen from Figure 12 that the maximum sin 2 ψ value of point Z (0) is 0.4 using the X-RAYBOT stress meter.
According to the selected ψ range, protect the last two values of 2θ in Fig. 14, and then perform linear fitting. The results are shown in Figure 17.
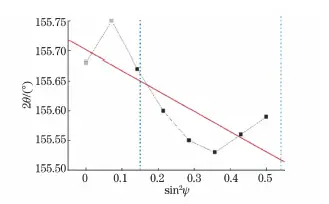
Fig. 17 Fitting results of 2θ-sin 2 ψ Z(0) curve measured by X-RAYBOT stress tester
Due to the texture of the material, its sin 2 The ψ curve is oscillatory.
The selected angle range ψ is different, resulting in differences in the slope and residual stress values obtained from the fitting line.
For materials with unknown texture and coarse grain, it is not advisable to choose a narrow ψ range and a small number of ψ stations for residual stress measurement, as this can lead to significant measurement errors.
Linear fitting may not be appropriate for materials with textured sin 2 ψ curves that are oscillatory.
During the measurement process, linear adjustment is often used to mitigate fluctuations caused by vibrations and measurement errors.
It may not be feasible to achieve an angle ψ of 45° as this may be influenced by the depth of penetration. A larger angle is more likely to produce more accurate results, as long as the depth of penetration can be ignored.
For coarse-grained or textured materials, the angle range ψ should be expanded as much as possible to eliminate the effects of nonlinear ε-sin. 2 ψ distribution. This can be achieved by measuring both angles ±ψ.
The accuracy of the fitted straight lines can be improved by using the least squares method to fit the regression and increasing both the interval ψ and the number of stations ψ. This will result in more reliable test values.
Measurement accuracy can also be improved by increasing the x-ray exposure area or increasing the number of participating diffraction grains through the swing method.
8. Conclusion
(1) The sin 2 ψ method can be used to determine the residual stress with greater accuracy by increasing the ψ range and selecting more ψ stations. However, this method has limitations as it involves single exposure, which can result in large measurement errors if the range of ψ is not sufficient.
(2) In measurement methods that use the sin 2 ψ principle, the roll method is superior to the tilt method. It is recommended to use the roll method whenever space conditions at the measuring point allow. To measure the residual stress in grooves of certain components, the coinclination method is commonly used.
(3) The true strain method is the preferred method for calculating residual stress.
(4) The sin2ψ method is considered a standard method for this purpose. To obtain more accurate results, the angle ψ should be defined using the sin 2 ψ-value bisection method and as many angles ψ as possible should be measured.