Chapter One: Introduction
1. Concept:
Supports lateral loads such as floor beams, crane beams, purlins, bridges, etc.
2. Classification:
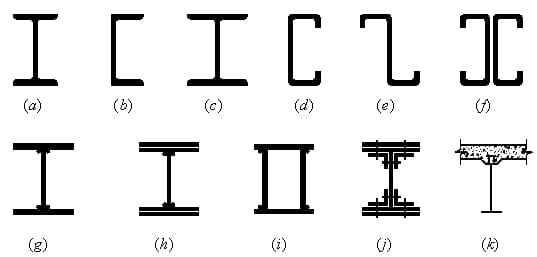
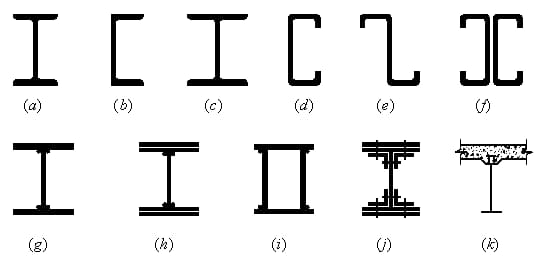
(1) Solid web:
H-shaped steel section: Easy to process, simple to manufacture and low in cost.
Composite section: When H-shaped steel cannot meet the strength and stiffness requirements.
(2) Lattic structure:
When the span exceeds 40m, it is best to use a trellis.
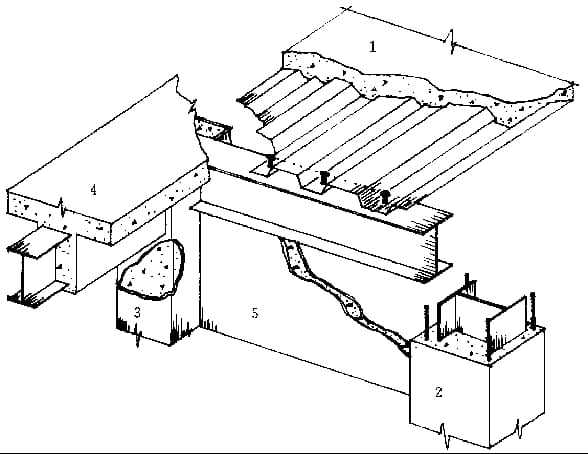
3. Beam Grid:
A flat system composed of main and secondary beams that intersect vertically and horizontally.
(1) Simplified beam grid: single main beam.
(2) Ordinary beam grid: Divided into main and secondary beams.
(3) Composite beam grid: Divided into main beams, horizontal and vertical secondary beams.
4. Interaction between beams and plates:
(1) Co-working: Mixed slab.
(2) Non-cooperative work: General reinforced concrete slab.
Chapter Two: Flexural strength.
The development of normal stress in the cross section can be divided into three phases:
(1) Elastic stage: Under dynamic load. ![]()
(2) Elastic-plastic stage: Under static load or indirect dynamic load.
(3) Plastic stage: ![]()
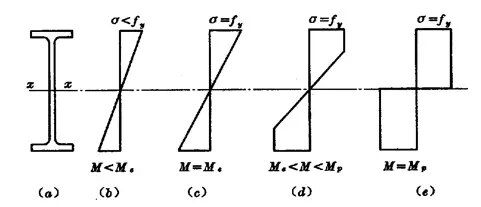
Bending capacity during the elastic-plastic phase of a section:
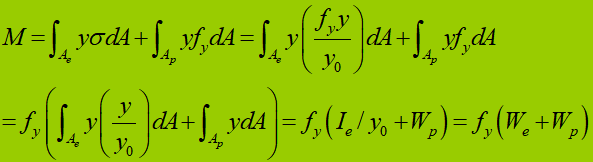
For a rectangular section:
(1) Elastic stage:
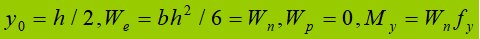
(2) Plastic stage:

(3) Elastic-plastic stage:
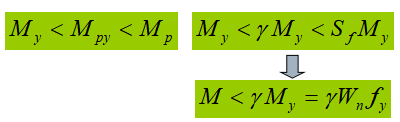
Section form factor:
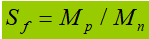
Chapter Three: Force Calculation Formulas Adopted by the Codes.
I. Normal bending stress:
Plastic development of partial section (1/4 section, a = h/8) as limit state:
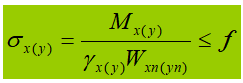
In the formula:
γ is the partial safety factor for the moment, which can be determined based on Table 5.1 of Section 5 of the design code.
There are two cases in which the partial safety factor for moment should be considered 1.0.
II. Shear force:

Method:
S :
Shear strength can be calculated using shear flow theory, assuming that it is uniformly distributed along the thin wall thickness direction.
(1) When calculating the vertical shear stress at any point in the web, it is necessary to calculate the moment of inertia of the gross sectional area above or below that point with respect to the neutral axis x.
(2) When calculating the horizontal shear stress at any point on the flange, it is necessary to calculate the moment of inertia of the gross sectional area to the left or right of that point about the neutral axis x.
Where t c is the thickness of the section at the location where the shear stress is being calculated.
III. Local buckling stress of the web:
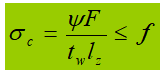
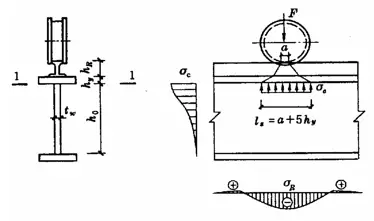
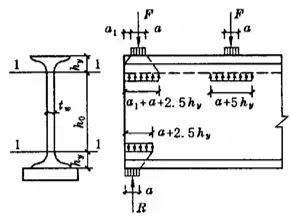
When the flange of a beam is subject to a large fixed central load (including support reactions) and no reinforcement is provided in accordance with Figure 5-5(a), or when it is subject to a concentrated live load (such as crane). pressure) according to Figure 5-5 (b), the local compressive strength at the edge of the web height must be calculated. Assuming that the concentrated load spreads from the point of application to a height range of h sim in the ratio of 1:2.5 and spreads in the ratio of 1:1 within a height range of h R , it is uniformly distributed along the height of the web edge calculation. The resulting σ c is very close to the maximum theoretical local pressure. Local compressive strength can be calculated by the following formula:

In the formula,
- F – concentrated load, which must be multiplied by the dynamic coefficient for dynamic loads;
- ψ – the amplification factor of the concentrated charge. For crane wheel pressure at heavy duty level, ψ = 1.35; for other loads, ψ = 1.0;
- l z – the assumed distribution length of a concentrated load at the calculated height of the web plate. For a load concentrated in the middle of the span, l z =a+5h yes +2h R ; for beam end support reaction force, l z =a+2.5h yes +um 1 ;
- a – the length of bearing a concentrated load along the span direction. For crane wheel pressure, when no data is available, 50 mm can be considered;
- h yes – the distance from the top of the beam to the calculated height of the web;
- h R – the height of the runway. If there is no track at the top of the beam, h R =0;
- a 1 – the distance from the end of the beam to the outer edge of the support plate, and its value must not exceed 2.5h yes .
When the calculation is not satisfactory, the fixed concentrated load or support of the bearing can be reinforced by installing transverse stiffeners or modifying the section size. However, when supporting concentrated moving loads, only the section size can be modified.
4. Equivalent voltage under complex stress state.
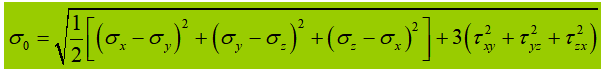
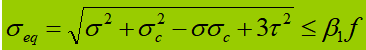
When the abdominal vibrator is subjected to significant normal stress, shear stress or local compressive stress at the calculated height, the equivalent stress at that location needs to be calculated.
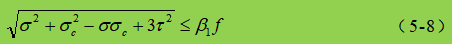
In the formula:
σ, τ, σ c – normal bending stress, shear stress and local compressive stress at the same point of the calculation height of the abdomen plate, positive for tensile stress and negative for compressive stress;
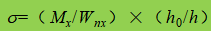
β 1 – coefficient to increase the design value of the compressive strength at a local point. When σ and σc have the same sign or σ c =0, β 1 =1.1; when σ and σc have opposite signs, β 1 =1.2.
Section Four: Calculation of General Beam Stability
1 . Basic concepts
General instability phenomenon:
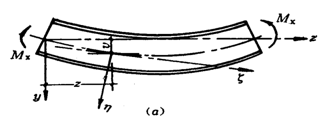
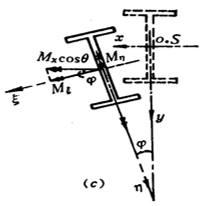
Mechanism analysis:
After the beam is deformed by bending, the upper flange is subjected to compression. Due to insufficient lateral stiffness of the beam, the beam will undergo lateral buckling deformation. In-plane bending deformation caused by moment also occurs along with torsional deformation due to uneven top-to-bottom bending of the beam section.
Therefore, the overall instability of the beam takes the form of flexural-torsional buckling or, more precisely, lateral-flexural-torsional buckling.
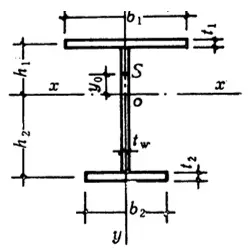
two . Calculation formula for critical bending moment of simply supported beam with uniaxial symmetrical cross section:
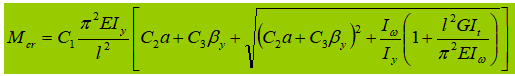
(1) C1, C2, C3 – Related to the type of load
(2) Iy, Iw, It – Moment of inertia of the cross section
(3) L – Length not braced in the lateral direction
(4) a – Location of the action point in the height direction.
(5) ![]()
| Load condition | Coefficient | ||
| G | C2 | G | |
| Load concentrated in the middle of the span | 1.35 | 0.55 | 0.41 |
| Load evenly distributed over the entire span | 1.13 | 0.46 | 0.53 |
| pure flexion | 1.00 | 0.00 | 1.00 |
The main factors that affect the overall stability of steel beams are:
(1) The unbraced length in the lateral direction or the distance L1 between the lateral support point of the compressed flange. The lower the value of L1, the better the overall stability of the beam and the greater the critical bending moment.
(2) The size of the cross section, including various moments of inertia. The greater the moment of inertia, the better the overall stability of the beam. In particular, increasing the width of the compressed flange b1 can also increase the value of βy in the formula.
(3) The restrictions on the section by the extreme supports of the beam. If the constraints on rotation about the y-axis of the section can be improved, the overall stability of the beam will be greatly improved.
(4) Loading type: Pure bending, evenly distributed load, load concentrated in the middle of the span.
(5) The location of the load action point along the cross-sectional height direction, a value; negative for the upper flange and positive for the lower flange.
3 . General stability check
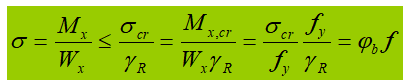
Single plane flexion:
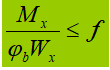
4 . Global Stability Coefficient
1. I-shaped welded cross section, biaxially symmetrical, pure bending load.
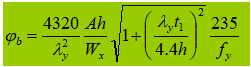
2. I-shaped, uniaxially symmetric welded cross section (effects of asymmetric cross section and different loads)
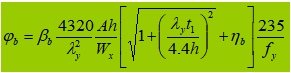
If φ b >0.6, the stability coefficient is considered as:

3. Beam simply supported in I-shaped laminated common steel.
4. Beam simply supported on a hot-rolled steel channel.
5. A double-axis I-shaped symmetrical cantilever beam.
5. Ensure overall stability.
The compressed flange of the beam is covered with a deck (reinforced concrete or steel plate) and firmly connected to prevent lateral displacement of the compressed flange.
For simply supported H-beams or I-beams, the relationship between the free length L1 and the width b of the compression flange does not exceed the value specified in Table 5.4.
Table 5.4: Maximum value of L1/b1 for which it is not necessary to calculate global stability for simply supported H-beams or I-beams.
| Steel Grade | A beam without lateral support points in the middle of the span. | Beam with flange subject to compression along the span and with lateral support points, regardless of where the load is applied. | |
| The load is applied to the flange. | The load is applied to the bottom flange. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
6. Checking steps for overall stability:
1. Determine if general stability check is required.
2. Calculate the section parameters.
3. Obtain the equivalent critical bending moment coefficient βb according to the loading conditions.
4. Substitute the values into the formulas to obtain the global stability coefficient ϕb and check the global stability.
Example: 5-2,5-3
Section 5 – Local stability and design of beam reinforcements
1. Overview:
Flange plate: Loading is relatively simple, and local stability is guaranteed by limiting the width-to-thickness ratio of the plate.
Web Plate: The load is complex and to meet the strength requirements, the section height is often large. If we continue to limit the height-to-thickness ratio of the web plate, the value of the web plate will be very large, which is not economical. Therefore, reinforcements are generally used to reduce the size of the plate and improve the bearing capacity of local stability.
1. Transverse reinforcements
2. Longitudinal reinforcements
3. Short stiffeners
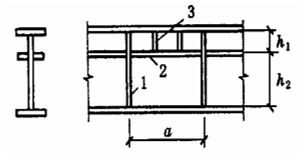
2. Local stability of the wing flange plate.
Design principle: Equal force principle.
According to the elastic design (with γ=1.0 for not considering plastic development), due to the influence of residual stress, the real cross section entered the elastic-plastic stage. The “Specification” takes E t =0.7E.
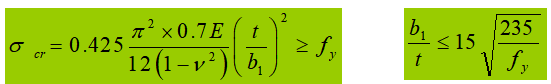
If plastic development is considered (γ > 1.0), plastic development will be greater, and E t =0.5E.
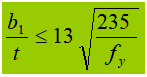
3. Web plate buckling
| No. | The condition of the web card. | Reinforcement Arrangement Specifications | |
| 1 |

|
σ τ =0 | Reinforcements can be omitted. |
| two | σ τ ≠0 | It is recommended to install transverse reinforcements that meet structural and calculation requirements. | |
| 3 |

|
It is recommended to install transverse reinforcements that meet structural and calculation requirements. | |
| 4 |
 The compressed flange is prevented from twisting. |
Longitudinal reinforcements must be added in the compression zone of the section where the bending stress is high, meeting structural and calculation requirements. | |
| 5 |
 The compressed flange can twist freely. |
||
| 6 | When necessary for calculation purposes. | ||
| 7 | When the local compressive stress is high. | If necessary, short reinforcements must be provided in the compression zone to meet structural and design requirements. | |
| 8 | On the beam support | It is advisable to install support reinforcements that meet structural and calculation requirements. | |
| 9 | Where the flange is subject to a large fixed concentrated load. | ||
| 10 | In any case |

|
|
1. Buckling of composite tension plates
Only the web plate with transverse stiffeners is configured.
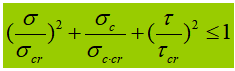
The web plate is configured with transverse and longitudinal reinforcements at the same time.
(1) Between compressed flange and longitudinal stiffeners.
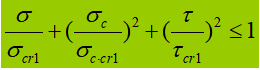
(2) Between the tension flange and the longitudinal reinforcements.
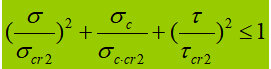
Short transverse stiffeners are installed between the compression flange and the longitudinal stiffeners.
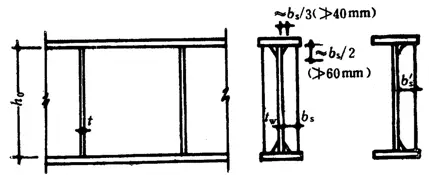
2. Construction requirements of web plate reinforcements
(1) Transverse steel reinforcements configured in pairs on both sides of the web.
Outward protruding width:
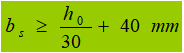
Thickness:
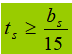
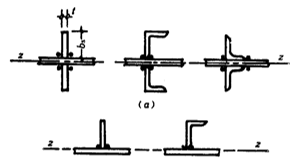
(2) Steel transverse reinforcements configured on one side of the web plate.
Protruding width outwards: must be greater than 1.2 times the value calculated according to the formula above.
Thickness: should not be less than 1/15 of the outwardly protruding width.
(3) In the web plate reinforced with transverse and longitudinal stiffeners, the longitudinal stiffeners must be disconnected at their intersections while the transverse stiffeners remain continuous.
The moment of inertia about the z axis must also satisfy:
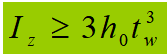
(4) End treatment of transverse reinforcements:
3. Reinforcements for support
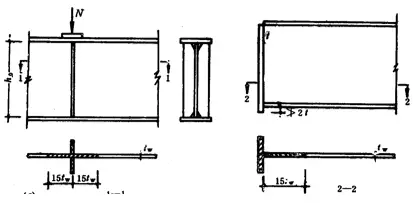
(1) Stability calculation:
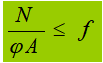
The stability of supporting reinforcements is calculated as a compressed element subjected to concentrated fixed loads or support reactions of the beam along its axis. The cross-sectional area A of this compression element includes both the reinforcement and the web plate area within 15t. c on each side of the reinforcement. The calculation length is approximately taken as h0.
(2) Calculation of compressive strength:
The end of the beam support reinforcements must be calculated according to the fixed concentrated load or support reaction that they support. When the end of the reinforcements is trimmed flat and tight, the compressive stress at the end face should be calculated as follows:
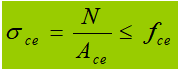
where:
- f ce is the design value of the compressive strength of the end face of the steel;
- The ce is the area where the support stiffeners contact the flange plate or top of the column.
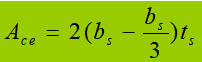
Design steps for web plate transverse reinforcements:
1. Determine whether it is necessary to install crossbars;
2. Install the beams and determine the spacing a, bs, ts;
3. Check the composite tension state of the core plate;
4. Check the support reinforcement: including welding (connection between cross members and web plate), axial compression stability check (out-of-plane z-axis stabilization) and strength check.
Example 5-3: Based on the conditions and results in Example 5-2, verify that the main beam section shown in Figure 5-9(b) meets the requirements. The main beam is a beam simply supported at both ends, made of Q235 steel and welded with E43 series manual welding electrodes.
Solution:
1. Main beam load capacity:
The simplified calculation diagram of the main beam is shown in Figure 5-9(a). The pressure exerted on the main beam by the secondary beams on both sides is 2×73.69+2×2.33=152.04 kN, and the pressure of the secondary beams at the end of the beam is half that of the middle secondary beam.
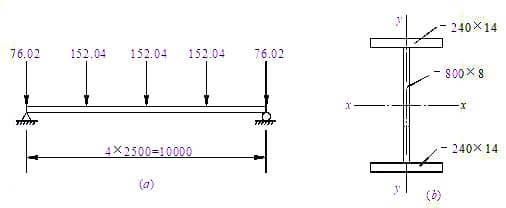
The support reaction of the main beam is R=2×152.04=304.08 kN.
The maximum bending moment of the beam is M=(304.08-76.02)x5-152.04×2.5=760.2 kN.m
2. Calculate the characteristics of the section:
H=131.2 cm², I x =145449 cm⁴, W x =3513.3 cm³. The self-weight of the main beam is 131.2×10²x7850x10⁻⁶x1.2=123.6 kg/m=1.211 kN/m. The factor of 1.2 is to account for the increased coefficient of main beam reinforcement. The calculated value of the bending moment after considering the weight of the main beam is M=760.2+1.2×1.211×10²/8=760.2+18.2=778.4 kN·m.
Considering the calculated value of the reaction force on the support after accounting for the self-weight of the main beam, it is R=304.08+1.2×1.211×10/2=304.08+7.27=311.3kN.
3. Strength check
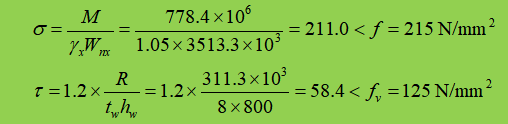
Support reinforcements are provided at the secondary beam connection and there is no local compressive stress. Furthermore, because the shear stress is relatively small, there is no need to check other converted stresses in the section.
4. On the secondary beam there is a rigid plate that guarantees the stability of the secondary beam and can serve as a lateral support point for the main beam.
At this point, as long as i 1 /b 1 =2500/240=10.4<16, the overall stability can be guaranteed without calculation.
5. Rigidity check
The total standard value of the load transmitted by the secondary beam is F T =(15.5+0.52)×7.5=120.2kN, therefore,
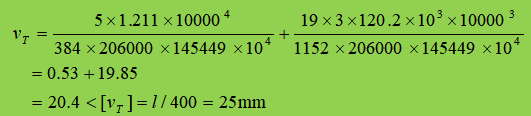
The total standard value of the load transmitted by the secondary beam is F P =2.5×4.2×7.5=78.75kN, therefore,
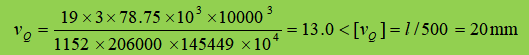
6. Local stability
Flange: b/t=(120-4)/14=8.3<13, which meets the local stability requirement, and γ x can be taken as 1.05; Web plate: h 0 / t c =800/8=100, transverse reinforcements need to be provided, details are omitted.
Section 6. Strength after buckling of thin plates
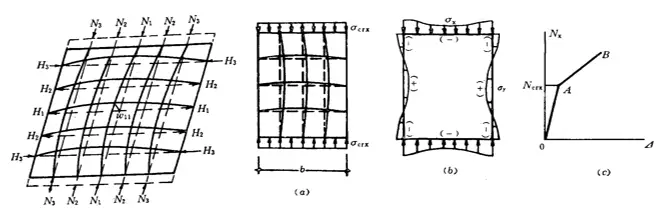
1. The concept and analysis of resistance after buckling of thin plates:
After buckling of the thin plate, transverse tensile stresses are generated in the middle of the plate, which further restricts the longitudinal bending deformation of the plate, allowing it to continue to withstand the increased pressure.
2. Analysis of the shear resistance capacity of the web plate considering the resistance after buckling:
1. Shear bearing capacity after buckling: Formula (5-94)

2. Shear bearing capacity includes two parts: Buckling shear force (buckling resistance) + stress field shear force (resistance after buckling).
3. Stress field shear force:
(1) Stress field method (complex);
(2) Code specification.
3. Analysis of the flexural resistance capacity of the web plate considering the resistance after buckling:
Whereas the bending resistance capacity of the web plate decreases slightly after buckling.
Two assumptions:
(1) Effective height;
(2) Symmetry between the tension zone and the compression zone.
The formula for calculating load capacity:

4. Calculation formula for beams considering resistance after buckling (subject simultaneously to bending moment and shear force):
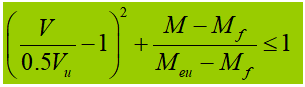
In the formula,
- M and V are the calculated values of the bending moment and shear force in the same cross section of the beam
- When V <0.5Vu, consider V = 0.5Vu
- When M < M f take M = M f
This indicates that:
(1) When M in section is less than M f that the flange can support, the web plate can withstand the shear force Vu;
(2) When V in the section is less than 0.5Vu, consider M = M UE .
5. Design of Transverse Reinforcements Considering Post-Buckling Strength
(1) If supporting stiffeners alone cannot satisfy Equation (5.99), paired transverse stiffeners should be added on both sides of the web to reduce the length of the buckling region.
(2) The cross-sectional dimensions of transverse reinforcements must meet the construction requirements of web reinforcements in accordance with Equation 5.85.
(3) According to the specifications of the steel structure, the central transverse reinforcement should be treated as an axial compression element, and its stability outside the web plane should be calculated based on the axial force using the following formula:
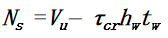
When reinforcement is subjected to a concentrated transverse load F, Ns must be increased by F.
Section 7. Design of Steel Beams
1. Design of Rolled Steel Beams
Calculate the design value of the maximum bending moment M max. to the beam based on actual conditions.
Determine the required section modulus based on flexural strength and overall stability:
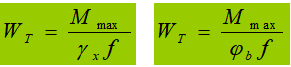
Determine the steel section based on section tables.
Section check:
(1) Resistance verification: bending, shear, local compression and equivalent tension.
(2) Stiffness check: check the deflection-span relationship of the beam.
(3) Verification of global stability (local stability of the steel section does not normally require verification).
(4) Adjust the section based on the verification results and perform the verification again until it meets the project requirements.
2. Section design of composite beams
1) Determine the required section modulus based on the loading conditions.
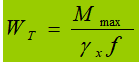
2) Determine the height of the beam:
- Minimum height: h min is determined by the stiffness of the beam.
- Maximum height: h max. is determined by architectural design requirements.
- Economic height: h and is determined by the minimum steel consumption.
Selected height: h min ≤ h ≤ h max. .
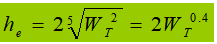
3). Determine the thickness of the web (assuming all shear forces are supported by the web), then:
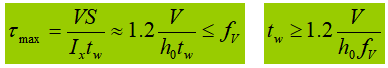
Alternatively, the web thickness can be determined using empirical formulas:
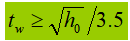
4). Determine the flange width:
After determining the web thickness, the flange area A f can be determined based on flexural strength requirements. Taking an I-shaped section as an example:
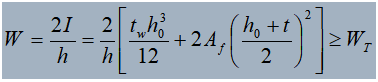
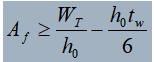
Once f is determined, b or t can be selected to determine the other value.
5). Section check:
- Resistance check: bending, shear, local compression and equivalent tensile strength.
- Stiffness check: check the deflection-span relationship of the beam.
- General stability check.
- Local stability check (flange plate).
- Adjust the section based on the scan results and run the scan again until it meets the project requirements.
- Calculate and organize reinforcements according to real conditions.
6). Calculation of Welds between Core and Flange
The connection weld is mainly used to resist bending shear, and the shear per unit length is:
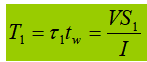
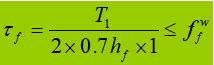
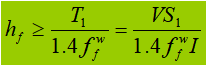
When the beam is subjected to a fixed concentrated load without supporting reinforcements, the upper flange weld supports both the shear force T 1 and concentrated force F. The force per unit length generated by F is V 1 :
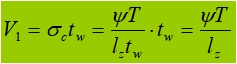
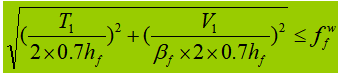
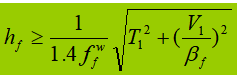
3. Section Change for Welded Composite Beams
Purpose: To save steel and deal with changes in bending moment.
Section change methods:
- Change the flange width.
- Change the flange thickness or number of layers.
- Change the height and thickness of the web.
Points to note:
- This method is only used for long spans.
- The section change must be gradual to avoid severe stress concentration.
- The equivalent voltage must be checked.
Section 8. Splicing of Steel Beams
1. Classification: factory splicing and on-site splicing.
2. Rolled steel sections: butt welding and splice plate welding.
3. In composite beam splicing: The web and flanges are staggered in the factory splicing. The web and flanges are spliced in the same section in the in-place splice.
Points to note:
- All splices should be arranged where the bending stress is relatively small.
- It is difficult to guarantee the quality of welding on site.
Section 9. Connection of Primary and Secondary Steel Beams and Beam Supports
1. Connection of primary and secondary metal beams: overlap and butt joint.
2. Beam Supports:
- Flat plate supports.
- Arch-shaped supports.
- Articulated supports.