Poisson's ratio of concrete is a very important parameter in stress and strain calculations. It represents the relationship between stress and tension.
Poisson's ratio cannot be derived from the direct relationship between stress and strain. There is a principle for calculating Poisson's ratio. This was invented by French mathematician Simeon Poisson.
The passion ratio can be calculated using the following equation proposed by Simeon Poisson.
ν = longitudinal deformation / transverse deformation
When a component is stretched in the longitudinal direction, stretching occurs in the transverse direction. The ratio between the longitudinal and transverse directions is calculated as Poisson's ratio.
When we calculate longitudinal stress, part of it is transferred as transverse stress. This relationship is established by the Poisson ratio. If the longitudinal stress of a section remains the same, Poisson's ratio is not necessary.
The specific Poisson's ratio is generally in the range of 0.15 to 0.25.
Poisson's ratio is taken into account when determining deformation and stress development in technical calculations. It is used as a constant when we calculate the stresses and deformations of elements such as beams, plates, shells, etc.


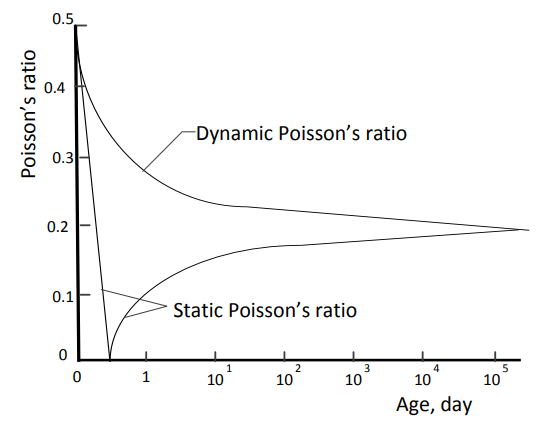
The figure above is from the research publication “The Effect of Mix Proportions and Method of Testing on
Poisson's ratio for mortar and concrete”. It appears that the Poisson's ratio of concrete changes over time. Although a high Poisson's ratio is observed in the initial phase of concrete, a rapid decline is observed with time.