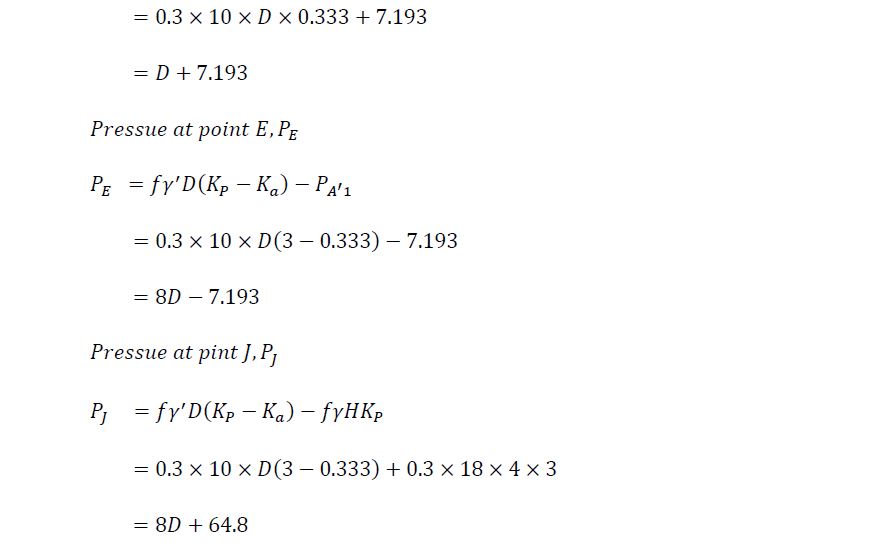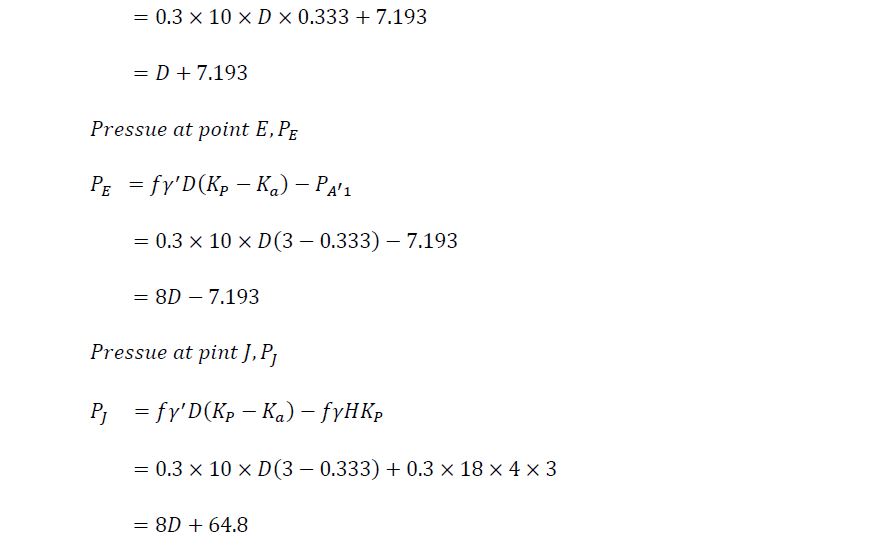Are you looking to build excavation safety systems?
Timber support system is a most commonly used method to protect excavated embankments in construction because it is more economical compared to other techniques. However, there are limitations such as lower support heights, so its application is limited to some extent.
In this article we discuss the analysis, design and detailing of the support system. The support system is intended to protect the excavated embankments and, above all, to minimize the impact on adjacent structures and falls from the embankments. The design process is expressed with a design calculation.
Design of excavation safety systems: practical example
Assumptions and parameters
The analysis and design considered the following assumptions and design data.
- Height at groundwater level from finished ground level 2 m
- Concrete density 25 kN/m 3
- Soil density 18 kN/m 3
- Density of saturated soil 20 kN/m 3
- Density of submerged soil 10 kN/m 3
- Water density 10 kN/m 3
- Angle of friction with the ground 30 0 (The average angle of friction is considered for well 01. Since the angle of friction of some layers is zero, the above values are assumed.
- Steel profile width 150mm
Structural arrangement of the support system
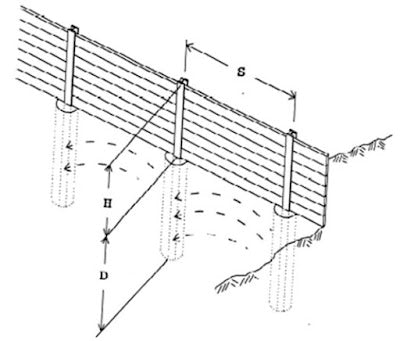
The steel profiles (H iron) are placed at a distance of 1.2 m to achieve a digging depth of 4 m. Steel plates are placed between the H iron bars to hold the earth in place.
Figure 01: Arrangement of the shoring system
Figure 02: Typical excavation detail
Structural analysis of support systems – excavation support systems
Structural analysis of the support system is performed in accordance with the California Trenching and Shoring Manual guidelines. The average friction angle is assumed to be 30.0 in this analysis. As the friction angle varies, average values are assumed in the design.
If the effective width is 1.2m above the excavator line, below the excavator line it will be 150mm (iron width H).
Therefore, the conversion method is considered to determine the equivalent effective width.
Furthermore, the arch effect is considered in this analysis to increase the bearing capacity of the H iron below the excavator line. Figure 03 shows the pressure distribution of the support system.
Figure 03: Pressure distribution
Payload and water pressure above the excavation line is not taken into account in the calculation, as this calculation is carried out to check whether this system is applicable to the proposed excavation depths.
The following factors were taken into consideration during the design
Adjust for bulging effect
Lump capacity = 0.08 φ (≤ 3.00)
Adjustment for stack width = (effective width) x 0.08 φ (≤ 1.00)
Curvature factor (f) = 0.08 φ (effective stack width)/ (stack spacing) ≤ 1.0)
Curvature factor (f) = 0.08 φ (effective stack width)/ (stack spacing) ≤ 1.0
Calculations
The following is the calculation method to determine the required embedding depth of the steel profile to withstand the active pressure exerted by the sole above the excavator line.
Calculation of design parameters
Angle of friction with the ground = 30 0
Ka = (1-Sin φ ) / 1+sin φ ) = (1-Sin 30) / 1+Sin 30) = 0.333
Kp = (1+Sin φ ) / 1-sin φ ) = (1+Sin 30) / 1-Sin 30 ) = 3,000
Lump capacity = 0.08 φ (≤ 3.00) = 0.08 x 30 = 2.4 <3
Adjustment for stack width = (effective width) x 0.08 φ (≤ 1.00) = 0.15 x 0.08 x 30 = 0.36 < 1
Curvature factor (f) = 0.08 φ (effective stack width)/ (stack spacing) ≤ 1.0 = 0.08 x 30 x 0.15 / 1.2 = 0.3
Density of submerged soil = γ sitting -γ I = 20 –10 = 10 kN/m 3
The designations shown in Figure 3 and Figure 3 apply to all designations mentioned herein.
Figure 04: Designations – pressure distribution