The bridge girder is generally constructed as a prestressed or post-stressed girder. In addition to prefabricated beams, concrete slabs are also constructed over abutments, box culverts, box girders and suspension bridges, those for passenger or vehicle traffic.
The prestressed concrete bridge girder design discussed in this article complies with BS 8110 Part 1.
In this article we discuss Design ULS (ULS estimation of bending moment capacity) a prestressed bridge girder with Strain Compatibility Method .
Let's discuss a little about the root compatibility method.


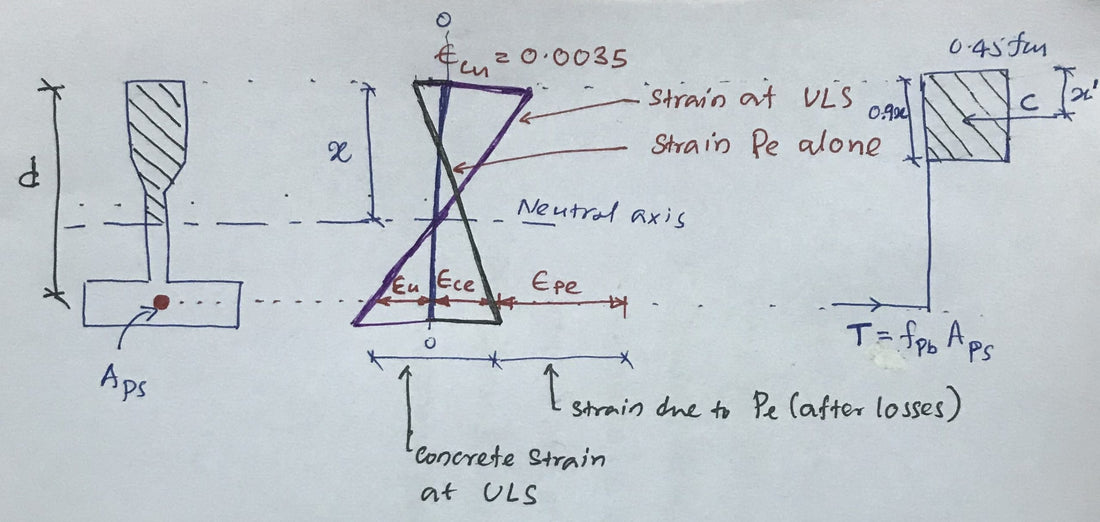
Ultimate limit state strain (ε pb )When selecting stress surfaces, pay attention to the following components.
- Elongation due to effective tensile force (Pe) (after losses) – ε Sports
- Deformation caused by the applied load – ε Pai
The elongation due to preload Pe is calculated as follows
ε Sports =P t / (A note: .E note: )
Where A note: is the area of the tendons and E note: is the elastic modulus of the steel.
During prestressing, the compression is below the neutral axis and the section is subjected to compressive stresses ε c and E ε Sports.
Here, ε ce is the compressive stress in the in-plane section of the steel through the “ Sports “.
The applied load initially causes this expansion ( ε ce ) to be zero, and then the tensile stress of the steel is developed. The total tensile stress developed by the load at the ultimate limit state is
ε Father = ε ce + ε Ela
Advance,
Reduction in concrete compressive stress = increase in steel tensile stress
This is because the steel and concrete are in the same section. The concrete stress decreases and at the same time the steel stress increases. Both happen at the same time.
Here,
ε ce =f with / E C = (P t /E C ) ( 1/A + e 2 /I)
ε Ela = ε cu (d – x) / x = 0.0035 (d – x) /x
The tensile stress of steel can be expressed as
ε pb = ε Ela + ε ce + ε Sports
We need to use an iterative process to calculate the depth of the neutral axis until the pushing force equals the pulling force (C = T).
After calculating the tensile strain (ε pb ), calculate the bending capacity of the section using the following equation.
M Ela =f pb A note: (t')
When calculating the bending capacity of the bridge beam, the following steps are performed.
- Assume a natural depth of the shaft and calculate the compression force (C = 0.45 fcu A' C )
- Next, calculate the tensile stress in the tendon.
- To do this, calculate the tensile stresses in the tendons ( ε pb = ε Ela + ε ce + ε Sports )
- And then you find the steel rhinestone on the stress-strain curve
- Check that the traction force ( T=f pb A note: ) and the compression force are the same.
- If not, repeat the calculation by changing the neutral axis depths until they are equal.
- After determining the depth of the neutral axis, calculate the bending capacity of the section ( M Ela =f pb A note: (dd')).
Let's explore this with a practical example
Bridge beam design data
- Wingspan = 16m
- Slab weight = 1 kN/m
- Payload = 4 kN/m
- Concrete density 24 kN/m 3
- Tension yield strength, f pu = 1670 N/mm 2
- Tendon area, A note: = 882mm 2
- Concrete cube strength, f cu = 40 N/mm 2
- Cross-sectional area, A = 121,000 mm 2
- Modulus of elasticity of steel, E note: = 205kN/mm 2
- Modulus of elasticity of concrete, E cu = 28 N/mm 2
- Cross-sectional area moment of inertia, I = 5.236×10 9 mm 4
- Preload force, P t = 744 kN


Calculate rated torque
Design load factors were adopted from BS 8110.
Section area = 121,000 mm 2
Self weight of the beam = 121,000 x 10 -6 x 24 = 2.9 kN/m
Design load = 1.4 (2.9 + 1) + 1.6 x 4 = 11.86 kN/m
Nominal torque = wl 2 /8 = 11.86 x 16 2 / 8 = 379.52 kN m
Moment resistance test
Calculate the depth of the neutral axis
Assume neutral axis, x = 400 mm from the uppermost outer fiber
Compressive stress block height = 0.9 x = 0.9 x 400 = 360mm


Compressive stress block area, A' C = ON 1 + UM 2 + UM 3
A' C = 150×200 + 0.5x(200+100)x75 + 135×100 = 54.75×10 3 millimeters 2
Compressive strength
C = 0.45.fcu.A' C
C = 0.45 x 40 x 54.75 x 10 3 = 985.5 × 10 3 N = 985.5 kN
Calculate traction force
T=f pb A note:
First we have to calculate the tensile stress (f pb ). We will use tension in this section.
ε pb = ε Sports + ε ce + ε Ela = P t /(A obs: .E obs: ) + (P t /E C )(1/A + t 2 /EU) + 0.0035(dx)/ x
ε Sports =P t /(A note: .E note: ) = 744×10 3 / (882×205×10 3 ) = 4.11 x 10 -3
ε ce = (P t /E C )(1/A + t 2 /l = ( 744×10 3 /28×10 3 ) ( 1/121000 + 199 2 /5.236×10 9 ) = 0.42 x 10 -3
ε Ela = 0.0035(dx)/x = 0.0035x ( (199+364) -400 ) / 400 = 1.43 x 10 -3
ε pb = 4.11 x 10 -3 +0.42×10 -3 + 1.43×10 -3 = 5.96×10 -3
The tendon elongation is 5.96 x 10 -3 ≈ 0.006
From the stress and strain diagram for cables in BS 8110 Part 01, the following information can be taken into account for design


The following information is available
- ϒ M = 1.5
- F pu = 1670 N/mm 2
- And note: = 205kN/mm 2
F pu /γ M = 1670 / 1.15 = 1452.2 N/mm 2
0.8f pu /γ M = 1452.2 x 0.8 = 1161.7 N/mm 2
F pu /γ M E note: = 1670 / (1.15 x 205×10 3 ) = 0.0071
0.8f pu /γ M E note: = 0.0071 x 0.8 = 0.0057
Now the values in the image above can be marked as follows.


Through linear interpolation we can determine the tension in the tendons.
F pb = 1175.3 N/mm 2
tendon area, A note: = 882 mm 2
Now we can calculate the pulling force,
T=f pb A note: = 1175.3 x 882 = 1036.6×10 3 N = 1,036.6 kN
C = 985.5 kN
T ≠ C, the assumed neutral axis depth is incorrect. We have to repeat the same procedure until T = C.
We may need to do several iterations to get close to the correct neutral axis depth.
First we check the neutral axis depth range.
We can assume C = 1036.6 kN (traction force) and then check the depth
C = 0.45.fcu.A' C
1036.6×10 3 = 0.45x40x A' C
A' C = 57588.9 mm 2
57588.9 = 150×200 + 0.5x(200+100)x75 + (0.9x – 150 – 75 )x100
x = 431.54 mm
Therefore we can say that “x” must be less than this value.
Suppose x = 425 mm
ε pb = 4.11 x 10 -3 +0.42×10 -3 + 0.0035x ( (199+364) -425 ) / 425 = 0.0057
Follow the same procedure as in the table above.
F pb = 1161.7 N/mm 2
T =f pb A note: = 1161.7 x 882 = 1024.6×10 3 N = 1,024.6 kN
C = 0.45.fcu.A' C = 0.45 x 40 x (150×200 + 0.5x(200+100)x75 + 157.5×100} = 1026×10 3 N = 1,026 kN
Therefore we can conclude that T ≈ C
So, to calculate the bending capacity, consider x = 425 mm.
M Ela =f pb A note: (t')
Where d' is the center of gravity of the compressive stress block.


d' can be calculated by calculating the moment about an edge. So the calculation is not taken into consideration because it is a simple calculation.
d' = 159.6 mm
Let's calculate the bending capacity.
M Ela =f pb A note: (t')
This equation can be written as follows:
M Ela = T (d – d')
M She = 1024.6 (563 -159.6)/1000 = 413.3 kN m
The bending capacity is 413.3 kNm and the applied bending moment is 379.52 kNm. The section is suitable for bending.
However, the section must be tested for shear. Information on sizing prestressed concrete beams can be found in a separate article.
The article Bridge Construction to BS 5400 could be consulted to provide more information on the theory of bridge girder design.
Further reading on precast concrete parts: Wikipedia article prestressed concrete could be forwarded.