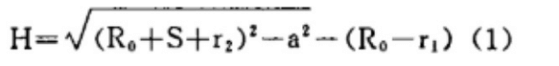Na fabricação de caldeiras e vasos de pressão, a tecnologia de conformação é um dos principais processos de fabricação.
No processo de conformação, a laminação da seção do cilindro é o método de conformação mais básico. Há muito trabalho envolvido na rolagem. A maior parte do processo de conformação é realizada em uma dobradeira simétrica de três rolos. No entanto, devido à espessura e ao diâmetro da secção do cilindro serem determinados de acordo com as diferentes condições do processo de produção, existe um número considerável de especificações e variedades.
A precisão da curvatura após a conformação depende do parâmetro “H”, que é a distância central entre os rolos superiores e inferiores no final da laminação.
Este parâmetro geralmente é determinado pela fórmula (1).
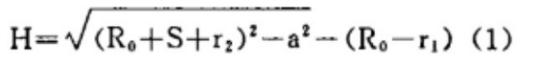
Pode parecer que esta fórmula não é complicada, mas para os fabricantes, a carga de trabalho cumulativa é considerável devido às diversas especificações e variedades de seções de cilindro.
Para simplificar e facilitar a determinação do valor de “H” sob diferentes condições, este artigo utilizará os dois algoritmos gráficos a seguir.
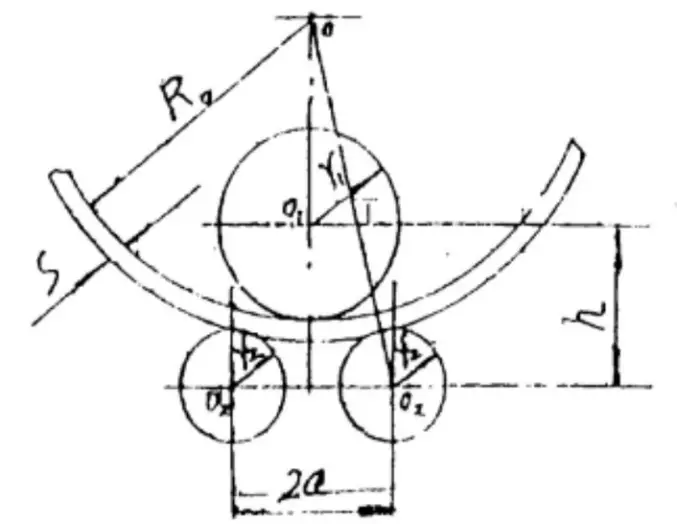
Fig. 1 O diagrama de posição final da dobradeira simétrica de três rolos
1. Um algoritmo gráfico para calcular o parâmetro “H” por “nomógrafo de cálculo da raiz quadrada da soma dos quadrados”
Quando um certo tipo de laminadora de chapas grossas é fornecido, os parâmetros a, r1 e r2 na fórmula acima são constantes, apenas s e R0 são variáveis.
Portanto, quando um determinado tipo de dobradeira de chapas é utilizado para laminar qualquer espessura e raio de curvatura, o parâmetro principal “h” correspondente pode ser obtido pelo seguinte algoritmo gráfico.
Primeiramente, um sistema de coordenadas retangular é estabelecido com a como ordenada e h como abscissa.
Em seguida, o seguinte desenho é realizado no sistema de coordenadas (mostrado na Fig. 2)
Deve interceptar OP = a no eixo longitudinal, tomar o ponto P como centro do círculo e tomar (R0 + S + r2) como o raio para formar um ponto positivo a no eixo transversal da interseção do arco.
Deve tomar o ponto a como o centro do círculo, tome R0 como o raio e reverso como um ponto B no eixo transversal do arco.
Então o ponto B é considerado o centro do círculo e R1 é tomado como o raio da intersecção do arco, e um ponto C na direção positiva do eixo transversal do arco é feito.
Assim: OC = h.
Por exemplo,
As seções do tambor com S = 20 mm e d = 2.000 mm são laminadas em uma dobradeira simétrica de três rolos 70 × 4.000.
Para calcular o valor de h.
De acordo com os dados, R1 = 350 mm, R2 = 330 mm, 2a = 800 mm.
De acordo com o algoritmo gráfico (mostrado na Fig. 2): h = 640mm, que é calculado pela fórmula:
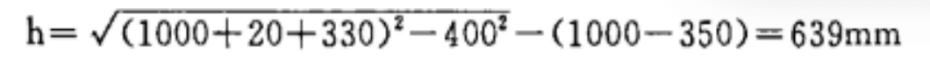
O erro absoluto é de apenas 1 mm, representando 0,015% do valor real, o que é bastante preciso.
Se (R + S + r) for transformado em uma régua móvel, é mais conveniente.
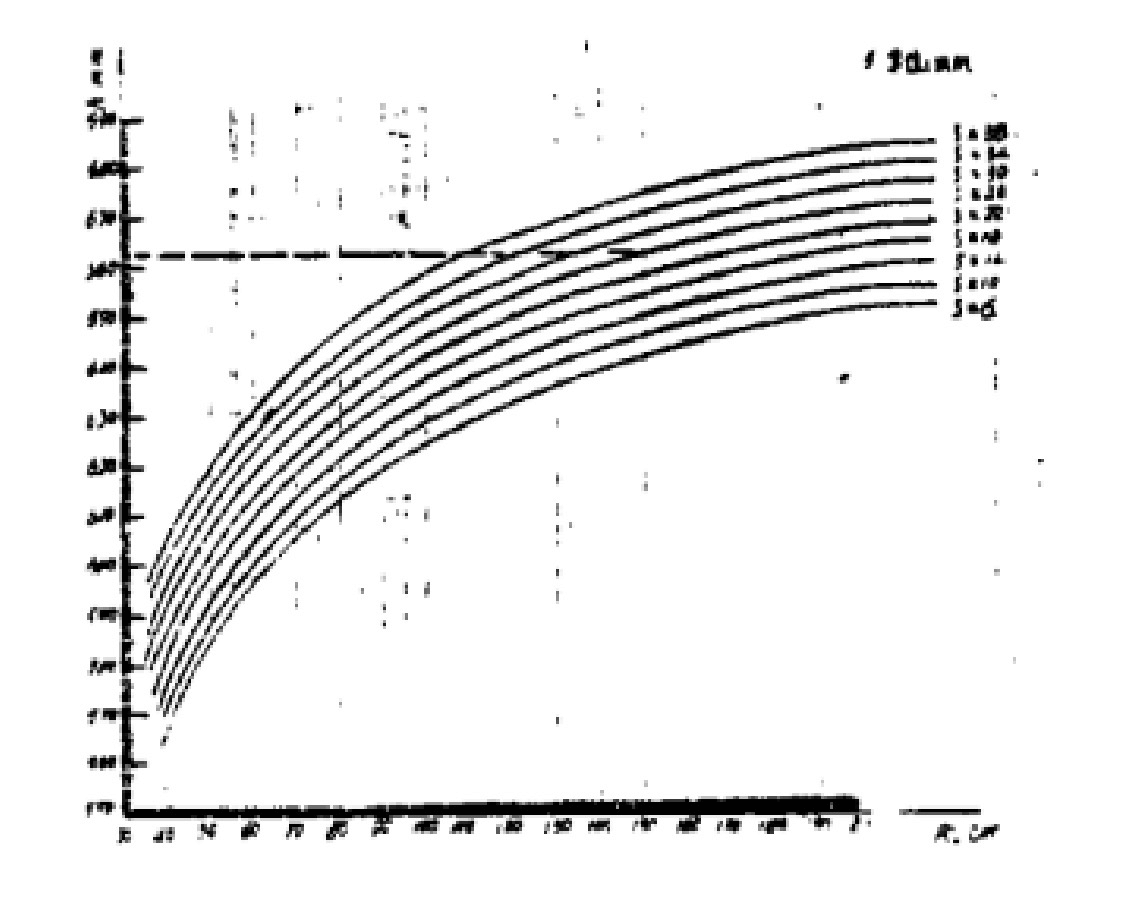
Fig. 2 Normograma para cálculo de “h”
2. Um algoritmo gráfico para calculando “h”de um certo tipo de máquina dobradeira simétrica de três rolos, que pode rolar o gráfico de ponto comum sob diferentes espessuras e raios de curvatura;
Como conhecido acima, quando um determinado tipo de dobradeira é fornecido, seus parâmetros a, R1 e R2 são fixos.
Então, se a curva de relacionamento de R0 e h sob diferentes espessuras de placa é desenhado em r0-h sistema de coordenadas, o gráfico de ponto comum de R0 e h de chapa de aço com diferentes espessuras neste tipo de laminadora podem ser obtidos.
É muito conveniente obter o valor do parâmetro principal “h” da seção do tambor neste tipo de calandra de chapas sob todas as diferentes condições.
A seguir está um diagrama de pontos comuns de uma dobradeira simétrica de três rolos 70 × 4000.
Conhecido: r1 = 350 mm, r2 = 330 mm, a = 400 mm
Então:
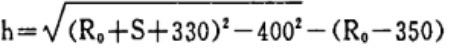
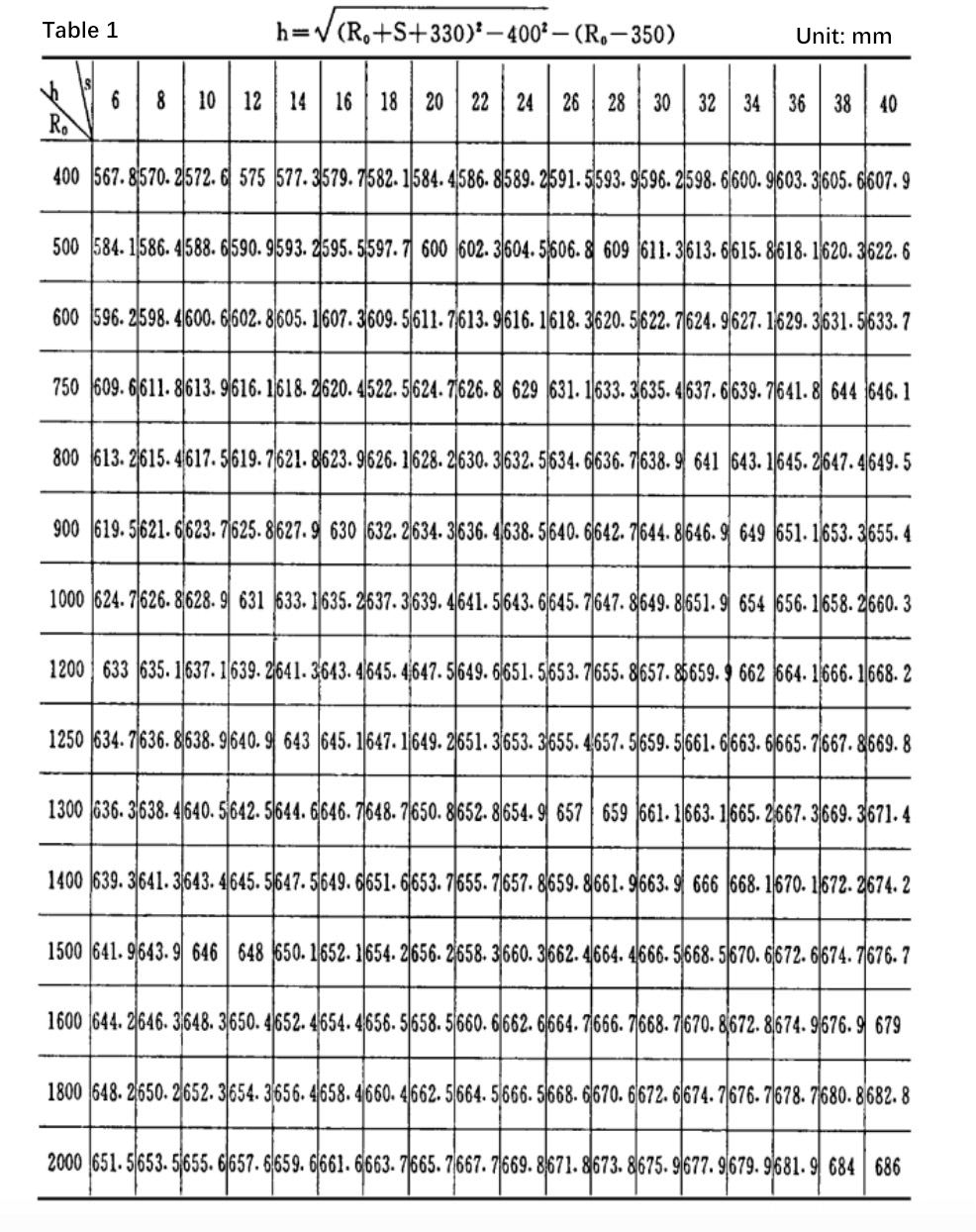
A Tabela 1 é a tabela de dados de cálculo e desenho com intervalo de 2mm.
De acordo com a experiência prática, a espessura da laminadora é geralmente 6 ≤ s ≤ 40 (mm).
Geralmente, o raio da seção do tambor rolante é 400 ≤ R0 ≤ 200 (mm).
Portanto, esse intervalo é usado como intervalo de desenho de cálculo.
Pode-se observar na tabela 1 que o valor de “n” é basicamente equivalente à espessura da chapa s quando um determinado tipo de dobradeira de chapa é utilizado para laminar uma determinada quantidade de R0.
O erro entre o valor real e o valor real é inferior a 0,05%.
No entanto, quando a placa de cobre é dobrada, ocorrem tanto deformação plástica quanto elástica.
Portanto, haverá uma certa recuperação elástica após o descarregamento.
Portanto, na produção real, o valor deve ser ligeiramente inferior ao valor real.
Desta forma, se utilizarmos a lei da variação equivalente das duas, o desenho será simplificado e o retorno elástico após a flexão real poderá ser compensado.
Ao mesmo tempo, a linha do gráfico pode ser reduzida e o valor “h” correspondente a qualquer S pode ser determinado sob um certo R0.
Conclusão
O primeiro algoritmo gráfico é universal, enquanto o último é para um determinado tipo de dobradeira de chapas, cujo tipo de dobradeira de chapas corresponde a um especial (kR0-S) gráfico de copontos.
Os resultados dos dois algoritmos gráficos no ensino são muito bons e esclarecem muito os alunos.
Em particular, o último método tem certa praticabilidade.
Sugere-se que o fabricante da dobradeira de chapas configure o diagrama principal comum de (nR0-S) na laminadora ou no manual, o que trará grande comodidade à própria produção do fabricante.