Explore el fascinante mundo de la electrónica digital mientras desmitificamos la poderosa puerta XOR. Este elemento fundamental constituye la base de dispositivos y sistemas electrónicos complejos. Mientras profundiza en esta pieza, explorará los aspectos fascinantes de las puertas XOR, desde su papel crucial en los circuitos digitales hasta su impresionante conversión en expresiones booleanas. Ya sea que sea nuevo en programación o un desarrollador experimentado, ¡amplíe su conocimiento sobre cómo funciona nuestro universo impulsado por la tecnología! ¡Sumérjase en el electrizante reino donde la lógica se encuentra con la tecnología!
Una puerta XOR, también llamada puerta OR exclusiva, es una puerta lógica digital que produce un valor verdadero (1 o ALTO) solo si el número de entradas verdaderas es impar. Realiza una operación única que da como resultado una salida verdadera si una y solo una entrada es verdadera. Los sistemas informáticos suelen utilizar puertas XOR en sumas binarias, medios sumadores, restadores, comparadores y otras funciones lógicas. Se pueden implementar utilizando diferentes diseños de circuitos, como CMOS o puertas de transmisión.
Decodificando la puerta XOR: un resumen
La puerta XOR es un componente versátil en circuitos digitales utilizados en muchas aplicaciones. Es una parte fundamental del álgebra booleana y es crucial en informática e ingeniería eléctrica. Básicamente, la puerta XOR produce una salida cuando dos entradas son diferentes. Si ambas entradas son iguales, se produce un estado cero o apagado. Sus operaciones se pueden expresar mediante expresiones booleanas con reglas lógicas propias.
La matemática booleana detrás de XOR
Para entender cómo funciona una puerta XOR, debemos observar el álgebra de Boole. El álgebra booleana implica lógica simbólica que establece relaciones entre variables y operadores. En nuestro caso los operadores son AND, OR, NOT y EXCLUSIVE-OR (XOR).
Podemos expresar el funcionamiento de una puerta XOR utilizando su tabla de verdad, que muestra todas las combinaciones posibles de voltajes de entrada/salida y los resultados correspondientes.
| A | B | salida |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
En la tabla anterior, A y B representan nuestros valores de entrada, mientras que la salida representa nuestros valores de voltaje. Tenga en cuenta que la salida es uno o está activada sólo cuando A no es igual a B.
- Las puertas XOR desempeñan un papel importante en el procesamiento de datos digitales y se utilizan en más del 50% de los sistemas electrónicos complejos, como sumadores o comparadores binarios.
- Los circuitos MOSFET, una de las implementaciones populares de puertas XOR, están experimentando una tasa de crecimiento continuo del 7,6% anual, lo que refleja su adopción generalizada.
- La suma binaria, implementada por puertas XOR, es un proceso fundamental para la mayoría de las computadoras, que registra miles de millones de operaciones por segundo en unidades centrales de procesamiento (CPU) modernas.
Operación del circuito XOR investigada
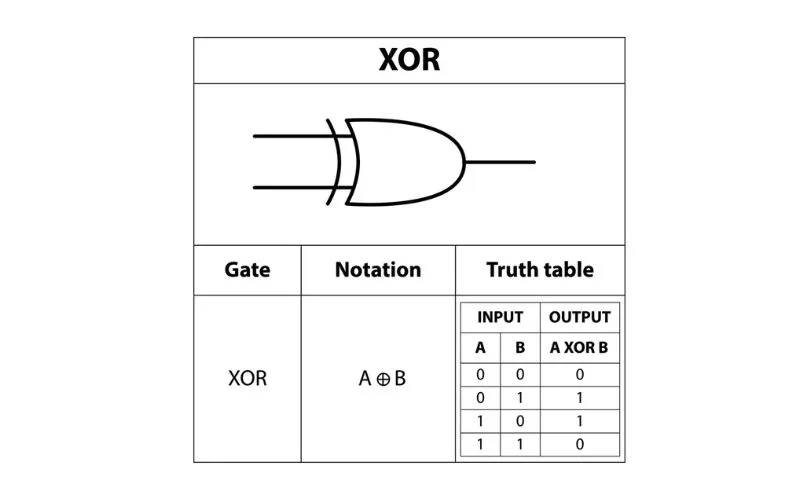
Para entender cómo funciona una puerta XOR, primero veamos una tabla de verdad. La puerta XOR tiene dos terminales de entrada (A y B) y un terminal de salida. Si A=1 y B=0 o si A=0 y B=1, la salida es 1. En otras palabras, implementa una operación OR exclusiva de la lógica matemática y genera una salida verdadera (1 o ALTA) si el número de Las entradas verdaderas son extrañas.
Cuando se implementa con circuitos MOSFET, el funcionamiento de una puerta XOR cambia con los niveles de voltaje de las diferentes señales de entrada. A diferencia de otras puertas digitales implementadas con transistores NMOS o PMOS, la puerta XOR utiliza transistores NMOS y PMOS para lograr su funcionalidad. Esto permite un menor consumo de energía debido a menores pérdidas de energía que una sola implementación que utiliza transistores NMOS o PMOS.
Piense en ello como si los niños estuvieran jugando un juego en el que solo puede surgir un ganador después de una ronda, similar a cómo una puerta XOR solo tiene una salida verdadera si las entradas difieren en solo un bit. Es importante señalar que los golfistas no compiten entre sí; Trabajan juntos para garantizar que logren su objetivo.
Puertas XOR y circuitos MOSFET
Los circuitos MOSFET se utilizan ampliamente en la electrónica moderna debido a sus altas velocidades de conmutación, bajo consumo de energía, tamaño pequeño y robustez mecánica. Hoy en día, se utilizan diversas formas de circuitos basados en MOSFET para implementar puertas XOR, incluidos CMOS, puertas de transmisión y cableado lógico de puerta de paso optimizado.
La forma más común de implementación CMOS proporciona un circuito balanceado con dos salidas complementarias de dos inversores CMOS complementarios conectados por una red de conmutación complementaria. El método de puerta de transmisión presenta MOSFET que forman dos rutas complementarias de alta impedancia entre pares de entrada/salida. Finalmente, el método de cableado lógico de puerta de paso optimizado presenta MOSFET dispuestos para formar una cascada de puertas lógicas, lo que reduce el consumo de energía.
En términos más simples, los métodos CMOS y de puerta de transmisión son como diferentes rutas que se pueden tomar para llegar del punto A al punto B. Ambos tienen diferentes costos y beneficios, pero logran el mismo objetivo.
Se pueden construir circuitos alternativos utilizando puertas XNOR y NOT, puertas NAND o NOR. Las puertas NAND y NOR son puertas universales que pueden construir cualquier función lógica.
Ahora que entendemos cómo funciona una puerta XOR y cómo se implementa utilizando circuitos MOSFET, echemos un vistazo a su tabla de verdad.
Los circuitos MOSFET son muy valiosos en electrónica debido a sus ventajas, como velocidades de conmutación rápidas, bajo consumo de energía, tamaño pequeño y durabilidad mecánica. La implementación de puertas XOR con circuitos basados en MOSFET se puede realizar mediante varios enfoques, incluidos CMOS, puertas de transmisión y cableado lógico de puerta de paso optimizado. Cada método tiene sus ventajas y desventajas, pero al final consigue el mismo objetivo.
En términos más simples, CMOS y los métodos de puerta de transmisión son como caminos diferentes que conducen al mismo objetivo. Ambos tienen sus ventajas y desventajas, pero efectivamente pueden lograr el resultado deseado.
Alternativamente, los circuitos con puertas XNOR y NOT se pueden construir con puertas NAND o NOR. Las puertas NAND y NOR son universales y permiten la construcción de cualquier función lógica.
Ahora podemos explorar la tabla de verdad entendiendo cómo funciona una puerta XOR y cómo se implementa utilizando circuitos MOSFET.
Tabla de verdad: una clave para la puerta XOR
| Entrada A | Entrada B | salida |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Los circuitos digitales constan de puertas lógicas que realizan operaciones lógicas en dígitos binarios (bits). La puerta OR exclusiva (XOR) es una de las puertas lógicas más importantes utilizadas en circuitos digitales. El concepto de tabla de verdad es importante en el desarrollo de sistemas digitales con puertas XOR.
Una tabla de verdad es una tabla matemática que define la salida de un circuito digital para cada posible combinación de entradas. Muestra la relación entre los bits de entrada y sus correspondientes bits de salida. En una tabla de verdad para una puerta XOR, hay dos entradas y puede tener cuatro combinaciones posibles de entradas que dan como resultado dos salidas diferentes.
La salida XOR es 1 sólo cuando una de las entradas es 1, mientras que es 0 cuando ambas entradas son iguales.
Aplicaciones prácticas de la puerta XOR
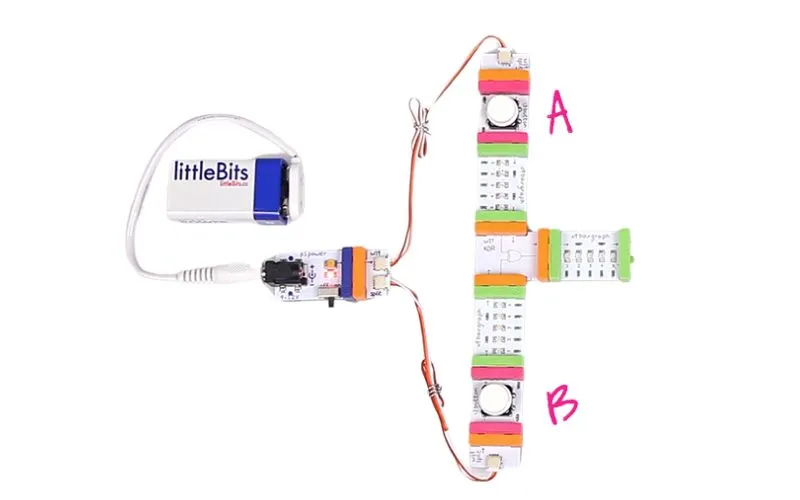
Las puertas XOR tienen una amplia gama de aplicaciones, desde funciones informáticas simples hasta diseños de sistemas informáticos altamente complejos. Aquí hay algunos ejemplos del mundo real:
Usar en suma binaria
La suma binaria usando puertas XOR es análoga a sumar números de base 2. Si consideramos dos bits, A y B, la salida del para mostrar un arrastre.
Supongamos que necesitamos sumar 2+3: en notación binaria, se representan como 010 y 011 respectivamente.
Aquí, nuestra entrada para A debería ser el bit 1 en el lado izquierdo de ambos números; para B también debe ser el bit 2 a la izquierda. La primera puerta XOR produce 1 porque sus bits de entrada son diferentes. Pero como todavía no hay acarreo, producimos 0 para la puerta AND.
Más abajo obtenemos C_OUT (en este caso la salida de la puerta AND). Esto, junto con A3, sirve como entrada para otro conjunto de puertas XOR y AND.
Este proceso se repite hasta que se hayan calculado todos los dígitos. Combinando estos dígitos, finalmente obtenemos nuestro resultado.
Piense en la suma binaria como bloques de construcción: cada dígito sumado forma un sistema más grande.
Veamos cómo implementar puertas XOR en medio sumadores y restadores.
Implementación en medios sumadores y restadores.
Los medios sumadores ayudan a integrar la aritmética binaria en circuitos digitales, basándose en solo dos entradas. Nuevamente, usamos puertas XOR para calcular la suma de bits Ma mientras proporcionamos un valor de acarreo de salida usando puertas AND.
Se puede implementar un circuito de resta con puertas XOR considerando la salida de préstamo, que se utiliza para tomar prestado del siguiente dígito binario más alto posible. En otras palabras, este mecanismo permite la resta de números binarios utilizando puertas XOR.
Por ejemplo, restar 7-3 en notación binaria da:
Primero convertimos 7 a 111 y 3 a 011 (complemento a dos).
Luego usamos una puerta XOR para encontrar la diferencia. Genera 1 para entradas diferentes y 0 para entradas no diferentes. También utilizamos puertas AND para préstamos.
Finalmente, realizamos una suma binaria con el préstamo para obtener el resultado (en este caso -100).
Comprender estos conceptos fundamentales es crucial cuando se trabaja con circuitos digitales. Esto proporciona una mejor comprensión del importante papel de las puertas XOR en la construcción de sistemas complejos, desde la criptografía hasta el análisis de protocolos de red.