En el tutorial anterior, se introdujo la aritmética booleana. Se mostró cómo se pueden sumar, restar, multiplicar y dividir números binarios. En este tutorial, ahora se discutirán las operaciones lógicas con números binarios. Las operaciones lógicas no son sólo la forma de implementar operaciones aritméticas (a través de circuitos combinacionales), sino que forman los componentes básicos de los circuitos digitales. Un circuito digital está construido mediante puertas lógicas donde las puertas lógicas realizan una u otra operación lógica booleana.
La información digital se almacena en un sistema informático de celda binaria. Una celda binaria es un dispositivo que puede tener un estado lógico ALTO o lógico BAJO y, por lo tanto, puede almacenar un bit de información. En un sistema de lógica positiva, el voltaje entre 2 V y 5 V como nivel de señal de entrada (en un puerto TTL) y 2,7 V a 5 V como nivel de señal de salida (desde un puerto TTL) se considera lógico ALTO y cualquier voltaje entre 0 V y 0,8 V. como nivel de señal de entrada (en un puerto TTL) y de 0 V a 0,5 V como nivel de señal de salida (desde un puerto TTL) se considera lógico BAJO. En un sistema lógico negativo ocurre lo contrario. Los niveles de voltaje entre los niveles lógicos ALTO y BAJO se denominan niveles de transición y los circuitos digitales (puertas lógicas) no responden a ellos.
Un grupo de celdas binarias se llama registro. Los registros se utilizan para almacenar información digital en un sistema informático (procesador o microcontrolador). Puede haber 8 bits (8 celdas binarias en un solo registro), 16 bits (16 celdas binarias en un solo registro), 32 bits (32 celdas binarias en un solo registro) o 64 bits (64 celdas binarias en un solo registro). ). ) se registra en un sistema informático de 8, 16, 32 o 64 bits, respectivamente. Los circuitos digitales buscan información binaria almacenada en registros y operan sobre ellos de acuerdo con sus circuitos digitales construidos por puertas lógicas, y luego almacenan el resultado nuevamente en otros registros.
El número binario almacenado en una celda o registro binario se puede tratar como una variable binaria o booleana. Las operaciones sobre estas variables booleanas (formadas por los dígitos 0 y 1) siguen un conjunto de reglas matemáticas que se conoce como álgebra booleana. Las operaciones sobre un conjunto de variables booleanas realizadas por un circuito digital se pueden expresar matemáticamente como una función booleana. Así, una función booleana está formada por constantes binarias, variables binarias y operadores lógicos. Las operaciones lógicas básicas del álgebra booleana son las operaciones Y, O y NO. Las operaciones AND, OR y NOT se realizan mediante puertas lógicas AND, OR y NOT respectivamente en un circuito digital.

Fig. 1: Imagen representacional de operaciones lógicas booleanas
Y operación –
La operación lógica AND es equivalente a la multiplicación de bits. Si se multiplican dos bits, si ambos bits son 1, solo el resultado será 1; de lo contrario, si uno de los bits es 0 o ambos bits son 0, el resultado es 0. En álgebra booleana, la operación Y se representa mediante un operador de punto o de ausencia. Supongamos que hay dos variables booleanas A y B, entonces el AND lógico entre A y B está representado por AB o AB. Si el resultado de esta operación AND se almacena en una variable Y, entonces se escribirá como AB = Y o AB = Y. Esto se leerá como 'A AND B es igual a Y'. Todos los resultados posibles de la operación AND entre dos variables de un solo bit A y B se muestran en la siguiente tabla de verdad:
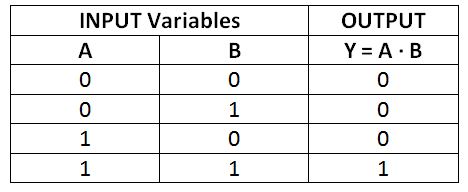
Fig. 2: Tabla de verdad de la operación AND
O Operación –
La operación lógica OR equivale a sumar bits. Si se suman dos bits, si ambos bits son 0, solo el resultado será 0; de lo contrario, si uno de los bits es 1 o ambos bits son 1, el resultado es 1. En álgebra booleana, la operación O está representada por el operador más. Supongamos que hay dos variables booleanas A y B, entonces el OR lógico entre A y B está representado por A + B. Si el resultado de esta operación OR se almacena en una variable Y, entonces se escribirá como A + B = Y . Esto se leerá como 'A O B es igual a Y'. Todos los resultados posibles de la operación OR entre dos variables de un solo bit A y B se muestran en la siguiente tabla de verdad:
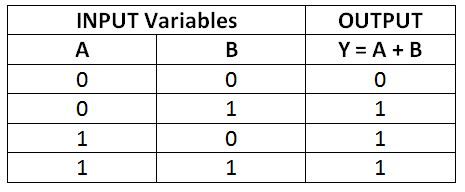
Fig. 3: Tabla de verdad de la operación OR
No operacion -
La operación NOT se aplica a un solo operando. Equivale a 1 complemento de una variable binaria. Si una variable booleana de un solo bit tiene el estado lógico 0, esa NO operación dará como resultado 1 y viceversa. Está representado por un número primo o una barra superior. Supongamos que si una variable booleana A se considera como operando, la operación NOT sobre ella estará representada por A' o Â. Si se almacena en una variable Y, se escribirá como A' = Y o  = Y. Se leerá como 'no A es igual a Y'. Dado que el operador not invierte los bits de la variable del operando, también se le llama inversor lógico. Todos los resultados posibles de la operación NOT en una variable A de un solo bit se muestran en la siguiente tabla de verdad – Operación NOT –
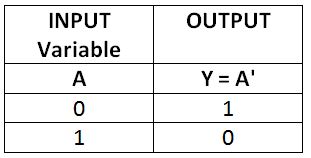
Fig. 4: Tabla de verdad de la operación NOT
Álgebra de Boole -
Las operaciones lógicas sobre variables booleanas siguen un conjunto de reglas que se conoce como álgebra booleana. Según las reglas del álgebra booleana, las variables booleanas combinadas con operadores lógicos (Y, O y NO) se pueden expresar como funciones booleanas. Y, O y NO son los operadores básicos del álgebra booleana. Cada expresión algebraica booleana (una función booleana) siempre se expresa en forma de operaciones AND, OR y NOT sobre variables booleanas. Puede haber una, dos, tres o cualquier número de variables booleanas en una función booleana o expresión algebraica booleana. Álgebra de Boole -
En la práctica, cada variable booleana representa un bit o una combinación en serie de bits en un sistema informático. Al implementar una serie de operaciones lógicas en un conjunto de variables booleanas (cada variable obtenida de una celda o registro binario) en una ruta de datos, el circuito digital realiza cálculos (aritmética binaria y, por lo tanto, álgebra binaria) en los datos de entrada (representados por variables booleanas). variables).
Suma booleana –
La suma booleana de bits individuales se realiza mediante la operación OR. Se rige por las siguientes reglas:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Se puede ver que la suma booleana en dos bits es igual a la operación lógica OR en ellos.
Multiplicación booleana –
La multiplicación booleana de bits individuales se realiza mediante la operación AND. Se rige por las siguientes reglas:
0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1
Se puede ver que la multiplicación booleana de dos bits es igual a la operación lógica AND sobre ellos.
Elogio booleano –
El complemento de una variable booleana se realiza mediante la operación NOT. Se rige por las siguientes reglas:
0' = 1
1' = 0.
Se puede ver que el elogio booleano (elogio de 1) en un bit es lo mismo que la operación lógica NOT en él.
Ahora bien, debe quedar claro que implementando operaciones lógicas (O, Y, NO), se pueden realizar operaciones aritméticas sobre números binarios (y por tanto sobre datos digitales). En el siguiente tutorial, aprenderá sobre las puertas lógicas múltiples . Las puertas lógicas realizan operaciones lógicas básicas (Y, O, NO) y otras operaciones lógicas (derivadas de Y, O y NO). Las puertas lógicas son los componentes básicos de un circuito digital. Cualquier expresión algebraica booleana o función booleana se puede expresar y minimizar a operaciones lógicas básicas entre variables booleanas (datos obtenidos a través de rutas de datos) que luego se pueden fabricar prácticamente en un circuito digital como interconexión entre puertas lógicas.

