Los humanos vivimos en un mundo analógico que estudian y entienden como un mundo digital.
Los humanos recopilan información sobre la naturaleza y la organizan como "ciencia". La base misma de la ciencia, es decir, el conocimiento organizado sobre la comprensión de la naturaleza y los fenómenos naturales, se basa en el lenguaje y las matemáticas. Cualquier rama de la ciencia implica la identificación de entidades, sus atributos, eventos asociados y el análisis matemático de estos atributos y eventos. Tal análisis estructural de la naturaleza y los fenómenos naturales comienza con la cuantificación de las cosas físicas y sus propiedades, es decir, la representación por nombre y propiedades de cosas y eventos como información discreta (palabras) y la medición de todas las propiedades posibles en números. Ésta es la naturaleza y el método básicos mediante los cuales los humanos exploran el mundo.
La electrónica tampoco tiene una forma diferente de representar, mantener y analizar la información. Cualquier información puede ser discreta, como nombres de cosas, eventos y propiedades, o puede ser continua, lo que requiere medición en comparación con una unidad estándar, cuantificación y representación en números.
La representación de información discreta requiere el uso de un lenguaje. Para representar información discreta como nombres de cosas, eventos y propiedades, cualquier lenguaje tiene un conjunto de símbolos que están organizados en un orden fijo y único y se pronuncian y escriben mediante un conjunto de reglas, de modo que una cosa, evento o su propiedad se identificado. por un nombre o palabra única.
Representar información continua requiere el uso de las matemáticas. Para representar información continua como la mayoría de cantidades físicas, se decide una unidad con la que se compara la entidad o evento continuo y la información continua se representa como un número seguido de la unidad.
Por lo tanto, para representar cualquier información en este mundo, primero es necesario tener un conjunto de símbolos y dígitos. Símbolos para formar palabras (sustantivos como nombres de cosas, sus propiedades, eventos y unidades) y dígitos para formar números. Así como los humanos hicieron esto usando el lenguaje y las matemáticas, en electrónica esto se hace con la electrónica digital.
La electrónica digital se ocupa de circuitos que pueden manejar sólo dos niveles de voltaje o corriente. Estos dos niveles de voltaje o corriente se denominan lógico alto y lógico bajo. La lógica alta se refiere a la presencia de suministro de energía total en una ubicación del circuito, y la lógica baja se refiere a la ausencia de voltaje, corriente o energía en una ubicación del circuito. Como idealmente no es posible alcanzar niveles de voltaje fijos, se acepta cierta tolerancia. La lógica de transistor a transistor que se utiliza para diseñar y fabricar circuitos integrados digitales reconoce cualquier voltaje entre 2 V y 5 V como nivel de señal de entrada (en un puerto TTL) y 2,7 V a 5 V como nivel de señal de salida (desde un puerto TTL). ). Gate) como lógica alta y cualquier voltaje entre 0 V y 0,8 V como nivel de señal de entrada (desde un puerto TTL) y 0 V a 0,5 V como nivel de señal de salida (desde un puerto TTL) como lógica baja. En escritura, la lógica alta se representa como 1 y la lógica baja se representa como 0. El símbolo más pequeño para representar información en electrónica digital es un bit. Un bit puede tener un estado Alto o Bajo. Un conjunto de cuatro bits se llama mordisco. Un nibble puede representar un máximo de 16 símbolos, es decir, 2^4. Un conjunto de ocho bits se denomina byte. Un byte puede representar 256 símbolos, es decir, 2 ^ 8. Se pueden utilizar varios bytes para representar más símbolos, dígitos o símbolos y dígitos. Estos símbolos y dígitos expresados digitalmente se pueden utilizar para representar información discreta (como palabras), así como cantidades mensurables (como números).

Fig. 1: Imagen representacional de la electrónica digital
Por lo tanto, la electrónica digital se ocupa de circuitos electrónicos que operan y manipulan en dos niveles de voltaje (ALTO y BAJO) y pueden realizar operaciones numéricas y lógicas en estos dos niveles de voltaje para procesar información del mundo real (representada simbólicamente como bits y bytes) con fines matemáticos. y estudio analítico. Dado que los circuitos digitales representan toda la información en bits que puede tener un valor de un conjunto de dos estados de voltaje (y que se puede representar matemáticamente mediante dos números 0 y 1), los circuitos y sistemas digitales son sistemas binarios. El conjunto de símbolos (para representar información) se denomina esquema de codificación o sistema de código en la electrónica digital y en los sistemas informáticos.
Por conveniencia, cualquier símbolo se puede representar como un número, y el conjunto de símbolos y dígitos para representar información en un sistema de código se puede expresar como un conjunto de números matemáticos. Cada número en un sistema de código o esquema de codificación se refiere a un único símbolo o dígito y puede expresarse en forma binaria, es decir, en forma de bits o bytes.
Se utilizan muchos sistemas numéricos, generalmente decimal, octal y hexadecimal. Los números de cualquier sistema numérico se pueden convertir al sistema binario y, por tanto, representarse en forma binaria y, por tanto, en forma electrónica digital. Los circuitos digitales se utilizan en todas las aplicaciones, desde computadoras, telefonía, procesamiento de datos, navegación por radar, instrumentos médicos y productos de consumo, dondequiera que se requiera el cómputo de algún tipo de información.
Por tanto, esta serie sobre electrónica digital comienza con la introducción de los sistemas numéricos y su conversión a números binarios. Recuerde que los números representan símbolos y dígitos en un sistema de códigos, y los símbolos y dígitos representan información y operaciones sobre esa información. Entonces, comencemos por comprender los sistemas numéricos.
Sistemas Numéricos –
Los números son una forma de representar la cantidad de cosas o una cantidad continua en comparación con una unidad estándar. Ha habido diferentes sistemas numéricos, de los cuales el sistema numérico decimal es el más común. El sistema numérico se refiere a la notación matemática de los números mediante un conjunto de dígitos (símbolos). Los dígitos en sí son símbolos especiales que representan números. Un sistema numérico se identifica por su base o raíz. En cualquier sistema numérico, un número está representado por la notación posicional de los dígitos. Una vez que el recuento aumenta más allá de la base o raíz en una posición en notación numérica, se aumenta el número en la siguiente posición en notación numérica. Entendamos esto por diferentes sistemas numéricos:
1) Sistema numérico decimal: el sistema numérico decimal consta de diez dígitos del 0 al 9. Estos dígitos se pueden usar para representar cualquier valor numérico, donde 10 se usa como base del sistema numérico decimal. Cada número en el sistema numérico decimal consta de dígitos ubicados en diferentes posiciones. En el sistema numérico decimal, cada columna de números enteros tiene valores de unidades, decenas, centenas, miles, etc., a medida que avanza el número de derecha a izquierda. Matemáticamente, estos números se escriben como 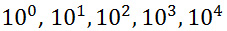
Figura 2: Potencias positivas de 10 en el sistema decimal
, . En esto, la izquierda del punto decimal representa el aumento en la potencia positiva de 10. De manera similar, para la parte del número fraccionario, el peso del número se vuelve más negativo a medida que se mueve de izquierda a derecha como 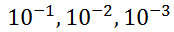
Fig. 3: Potencias negativas de 10 en el sistema decimal
.
El valor de cualquier número decimal será igual a la suma de sus dígitos multiplicada por sus respectivos pesos. Por ejemplo, si N = 7245 en formato decimal es igual a
7.000 + 200 + 40 + 5
Donde también se puede escribir como,
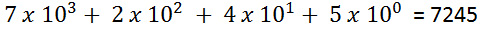
Fig. 4: Pesos de un número decimal
Del ejemplo anterior, en el sistema numérico decimal, donde el bit más a la izquierda es el bit más significativo (MSB) y el bit más a la derecha es el bit menos significativo (LSB).
El sistema numérico decimal es el sistema numérico adoptado en todo el mundo para el cálculo matemático debido a su facilidad de uso. Con base 10, es fácil realizar operaciones aritméticas en este sistema numérico ya que es fácil recordar hasta 10 símbolos (dígitos) para representar números y, al escribir, el cálculo en números decimales se vuelve fácil debido al simple incremento y decremento posicional. También se cree que debido a que los humanos tienen 10 dedos, el sistema numérico de base 10 se volvió obvio de usar.
Sin embargo, la popularidad del sistema decimal debe atribuirse al concepto de cero. El cero se introdujo por primera vez sólo en el sistema decimal. Fue un concepto revolucionario representar el vacío o la nada. El cero permitía representar ningún peso en una posición en la notación numérica de un número. Esto hizo que fuera mucho más fácil realizar operaciones aritméticas con números (principalmente multiplicaciones), que antes probablemente estaban más allá de la imaginación.
2) Números Binarios – El sistema numérico binario es simple porque consta de sólo dos dígitos, es decir, 0 y 1. Así como el sistema decimal con sus diez dígitos es un sistema de base diez, el sistema binario con sus dos dígitos es un Los dígitos de base dos son un sistema de base dos. La posición 0 o 1 en un número binario indica su "peso" dentro del número. En un número binario, el peso de cada posición sucesivamente más alta a la izquierda es una potencia creciente de dos.
En el sistema numérico binario, un número binario como 101100101 se expresa con una secuencia de unos y ceros, y cada dígito de la secuencia se mueve de derecha a izquierda y tiene un valor dos veces mayor que el del dígito anterior. Pero al ser un dígito binario solo puede tener el valor 1 o 0, por lo tanto, q es igual a 2 y su posición indica su peso dentro de la cadena.
Como se ve en el sistema numérico decimal, el peso de cada dígito a la izquierda aumenta en 10, también en el sistema numérico binario, el peso de cada dígito aumenta en el factor 2. El primer dígito tiene el peso de 1 (2 0 ). , el segundo dígito tiene un peso de 2 (2 1 ), el tercer dígito tiene un peso de 4 (2 2 ) y el cuarto dígito tiene un peso de 8 (2 3 ).

Fig. 5: Equivalentes decimales en el sistema numérico binario
En el sistema digital, cada uno de los dígitos binarios se denomina bit y los grupos de 4 y 8 bits se denominan nibble y byte, respectivamente. El número decimal más grande que se puede representar mediante un número binario de n bits es 2n – 1 (comenzando con cero). Así, con un número binario de 8 bits, el número decimal máximo que se puede representar es 2 8 – 1 = 255.
Los números binarios son importantes porque representan un número en 0 o 1. De esta manera representan un número en bits (o bytes) que es la forma que utilizan los circuitos electrónicos digitales.
3) Números octales: el sistema numérico octal utiliza los dígitos 0, 1, 2, 3, 4, 5, 6 y 7. La base del sistema octal es ocho. Cada posición significativa en un número octal tiene un peso posicional, y la posición menos significativa tiene un peso de 80. Las posiciones significativas más altas reciben un peso en el proceso ascendente de ocho. El equivalente octal de un número decimal se puede obtener dividiendo un número decimal dado por 8 repetidamente hasta obtener un cociente de 0.
Los números octales son importantes a su manera. Usando números octales, un número binario representado en bytes se puede escribir y expresar como un conjunto de tres dígitos en el sistema numérico octal. Los números octales fueron muy útiles para representar números binarios de manera concisa en algunas de las primeras computadoras que usaron palabras de 12, 24 y 36 bits. Una palabra de 12 bits se puede representar fácilmente mediante un número octal de cuatro dígitos, donde cada dígito del número octal representa los tres dígitos de la forma binaria de la palabra de 12 bits. Por ejemplo, una palabra de 12 bits puede tener un valor decimal máximo: 4095, que puede representarse en el sistema numérico octal como 7777. El '7-7-7-7' es una representación concisa de la palabra de 12 bits: 111 -111 -111- 111 donde cada dígito octal se puede convertir directamente a forma binaria.
4) Números hexadecimales: el sistema numérico hexadecimal tiene una base de 16 y utiliza 16 símbolos, a saber, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Los símbolos A, B, C, D, E y F representan los decimales 10, 11, 12, 13, 14 y 15 respectivamente. Cada posición en un número hexadecimal tiene un peso posicional. La posición menos significativa tiene un peso de 16 0 . Las posiciones más significativas reciben ponderaciones en potencias ascendentes de dieciséis 16 1 16 2 ,16 3 .
Cuando las computadoras comenzaron a usar palabras de 8, 16 y 32 bits, los números hexadecimales se convirtieron en una forma de representar de manera concisa su representación binaria. Así, una palabra de 8 bits puede tener un valor máximo de 255, que en hexadecimal se puede representar como FF. El 'FF' es una representación concisa de la palabra de 8 bits: 1111-1111, donde cada dígito hexadecimal se puede convertir directamente a formato binario.
Conversiones del sistema numérico –
Los humanos usan números decimales y las computadoras usan números binarios. Por lo tanto, es útil convertir números decimales en números binarios, números octales (representación concisa de palabras binarias de 12, 24 y 36 bits) y números hexadecimales (representación concisa de palabras binarias de 8, 16 y 8 bits). palabras binarias de 32 bits). palabras binarias). A veces, es posible que también sea necesario convertir los números binarios, octales y hexadecimales a números decimales. A veces, es posible que también sea necesario convertir los números octales y hexadecimales a números binarios y viceversa.
1) Conversión de decimal a binario: un método sencillo para convertir un número decimal a un número binario es dividir el número decimal por 2 progresivamente, hasta obtener el cociente de cero. El número binario se obtiene considerando el resto de cada división en orden inverso. El procedimiento para convertir decimal a binario se describe en el siguiente ejemplo:
Convirtiendo el número decimal 53,625 en un número binario equivalente –
El número decimal 53,625 tiene dos partes: entero (53) y fracción (0,625).
· Conversión de enteros:
Resto de la división
2) 53
2) 26 1
2) 13 0
2) 6 1
2) 3 0
2) 1 1
2) 0 1 a MSB
Leer el resto desde abajo da el equivalente binario. Entonces (53)10 = (110101)2.
· Conversión fraccionaria:
Si el número decimal es una fracción, su equivalente binario se obtiene multiplicando continuamente el número por 2, anotando el acarreo en la posición entera cada vez. Los transportes en orden directo proporcionan el número binario requerido.
Multiplicación de números enteros
0,625 x 2 = 1,25 1àMSB
0,250 x 2 = 0,50 0
0,500 x 2 = 1,00 1
0,000 x 2 = 0,00 0
No es posible realizar más multiplicaciones por dos porque el producto es cero. El equivalente binario se obtiene leyendo los términos de transporte de arriba a abajo. Por tanto, (0,625)10 es (0,101)2. El número combinado dará el equivalente binario como (53,625)10 = (110101,101)2.
2) Conversión de decimal a octal – La conversión de decimal a octal se puede realizar de la siguiente manera –
Por ejemplo, para convertir (444,456)10 a un número octal,
Conversión de números enteros:
Resto de la división
8) 444
8) 55 4
8) 6 7
8) 0 6
Leyendo los restos de abajo hacia arriba, el número decimal (444)10 equivale al número octal (678)8.
Conversión fraccionaria:
Multiplicación de números enteros
0,456 x 8 = 3,648 a 3
0,648 x 8 = 5,184 a 5
0,184 x 8 = 1,472 por 1
0,472 x 8 = 3,776 a 3
0,776 x 8 = 6,208 a 6
El proceso finaliza cuando se obtienen dígitos significativos. Por tanto, el equivalente octal de (444,456)10 es (674,35136)8.
3) Conversión de decimal a hexadecimal: el número hexadecimal se puede obtener dividiendo el número decimal dado por 16 repetidamente. Por ejemplo -
Conversión (115)10. para número hexadecimal,
Resto de la división
16) 115 –
16) 7 3
16) 0 7
Leyendo los restos de abajo hacia arriba, el número decimal (115)10 equivale al número hexadecimal (73)16.
4) Conversión de binario a decimal: un número binario se puede convertir en un número decimal multiplicando los números binarios 1 o 0 por su peso y sumando los productos. Por ejemplo, convertir el número binario (101111.1101)2 en su equivalente decimal se puede hacer de la siguiente manera:
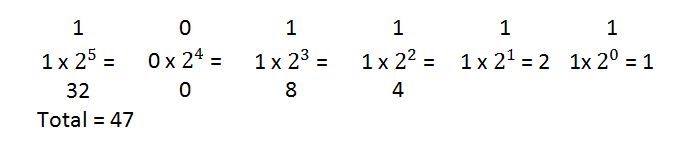
Fig. 6: Imagen que muestra la conversión de binario a decimal
Por lo tanto (101111)2 se puede escribir como (47)10. totales = 47
La conversión de (0.1101)2 se realiza de la siguiente manera:
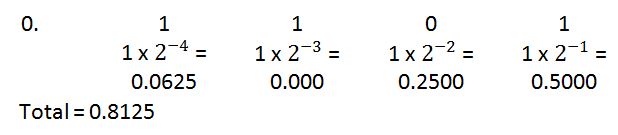
Fig. 7: Imagen que muestra la conversión de fracción binaria a decimal
Por tanto, (0,1101)2 es igual a (0,8125)10. Y entonces, (101111,1101)2 es igual a (47,8125)10. Total = 0,8125
5) Conversión de octal a decimal: la conversión de un número octal a decimal se puede realizar multiplicando cada dígito significativo del número octal por su peso respectivo y sumando los productos. Por ejemplo, el número octal (237)8 se puede convertir a decimales de la siguiente manera:
(237)8 = 2×2 2 +3×2 1 +7×2 0
= 2×64 + 3×8 + 7×1
= 128 + 24 + 7
= (159)10
6) Conversión de hexadecimal a decimal – La conversión de un número hexadecimal a decimal se puede realizar multiplicando cada dígito significativo del hexadecimal por su respectivo peso y sumando los productos. Por ejemplo, el número hexadecimal A3BH se puede convertir a un número decimal de la siguiente manera:
A3BH = (A3B)16 = A x 16 2 +3 x 16 1 + B x 16 0
= 10 x 2 2 +3×2 1 + 11 x 2 0
= 10x256 + 3x16 + 11x1
= 2560 + 48 + 11
= (2619)10
7) Conversión de octal a binario y de binario a octal: la conversión de octal a binario y de binario a octal es útil cuando es necesario representar palabras binarias de 12, 24 o 36 bits. Cada dígito octal es una representación directa de tres dígitos del número binario. Por ejemplo, 7777 equivale a 111-111-111-111.
8) Conversión de hexadecimal a binario y de binario a hexadecimal: la conversión de hexadecimal a binario y de binario a hexadecimal es útil cuando es necesario representar palabras binarias de 8, 16 o 32 bits. Cada dígito hexadecimal es una representación directa de cuatro dígitos binarios del número binario. Por ejemplo, FF equivale a 1111-1111.
Código de caracteres ASCII –
Los sistemas de códigos son conjuntos fijos de símbolos (incluidos dígitos) que se pueden utilizar para representar información. El Código Estándar Americano para el Intercambio de Información (ASCII) es el formato más común para archivos de texto en computadoras e Internet. En un archivo ASCII cada carácter alfabético, numérico o especial está representado por un número binario de 7 bits, por lo tanto en este sistema se pueden representar 128 símbolos (caracteres). Los sistemas operativos basados en UNIX y DOS utilizan ASCII para archivos de texto. ASCII fue desarrollado por el Instituto Nacional Estadounidense de Estándares (ANSI).
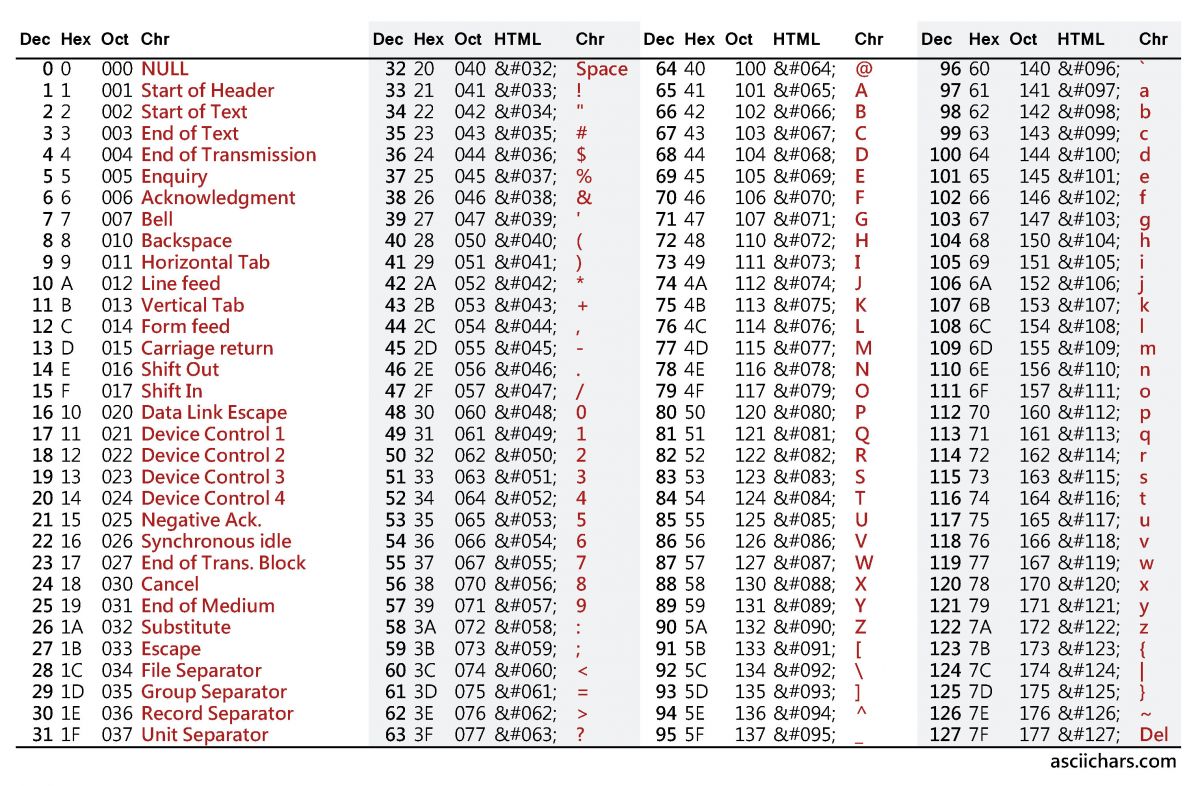
Fig. 8: Tabla con códigos de caracteres ASCII
Unicódigo –
El código de caracteres ASCII sólo se puede utilizar para representar información en alfabeto inglés, dígitos decimales y algunos caracteres especiales. Por lo tanto, era necesario un código que pudiera acomodar caracteres y símbolos de otros idiomas y escrituras. El estándar mundial de caracteres Unicode es un sistema para “el intercambio, procesamiento y visualización de textos escritos en los distintos idiomas del mundo moderno. El estándar Unicode contiene 34.168 caracteres codificados distintos derivados de 24 escrituras de idiomas compatibles.
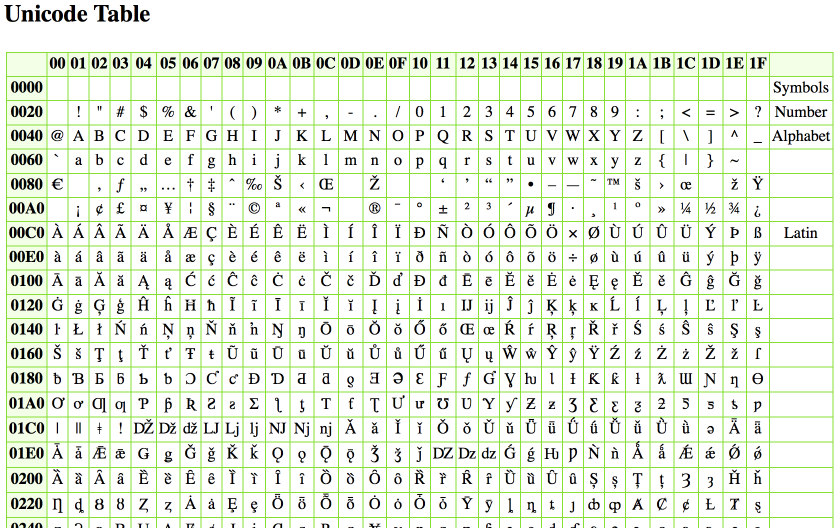
Fig. 9: Tabla que enumera los símbolos y códigos Unicode
Código EBCDIC –
El código de intercambio decimal codificado en binario extendido (EBCDIC) es un código binario para caracteres alfabéticos y numéricos que IBM desarrolló para sus sistemas operativos más grandes. Es el código para archivos de texto utilizados en el sistema operativo OS/390 de IBM para sus servidores S/390. En un archivo EBCDIC, cada carácter alfabético o numérico está representado por un número binario de 8 bits y puede haber un máximo de 256 símbolos representados.
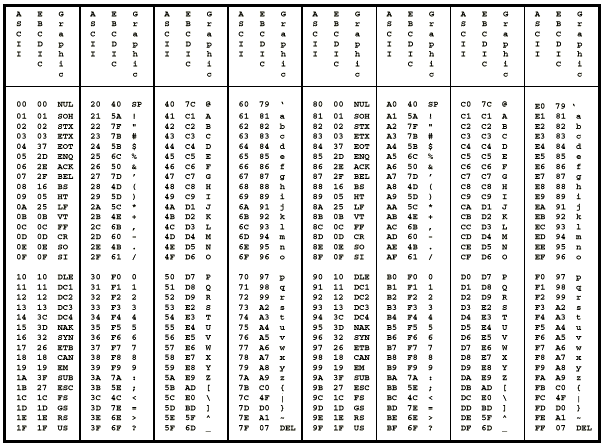
Fig. 10: Tabla que enumera los caracteres y códigos EBCDIC
En el siguiente tutorial, aprenderá sobre operaciones aritméticas con números binarios.

