Para comprender mejor la funcionalidad y el rendimiento de un filtro, existen funciones matemáticas que teóricamente representan un filtro, como la función de transferencia, el factor de calidad y la frecuencia de corte. Comprender estos términos facilitará la comprensión de una propiedad de filtro.
Terminologías (definiciones)
Función de transferencia: las entradas y salidas de un circuito amplificador operacional pueden ser voltajes, corrientes o una combinación de ambos. Cuando se utilizan números complejos para cantidades de entrada y salida, la relación entre salida y entrada se convierte en una función de la frecuencia. El nombre del motivo es función de transferencia.
Transformada de Laplace: la transformada de Laplace se utiliza para resolver ecuaciones diferenciales, la transformada de Laplace convierte la ecuación diferencial en un problema algebraico que es relativamente fácil de resolver.
Sistema variante en el tiempo: el retraso o avance del tiempo en la señal de entrada cambia no solo la salida, sino también el resto de parámetros.
Función de transferencia
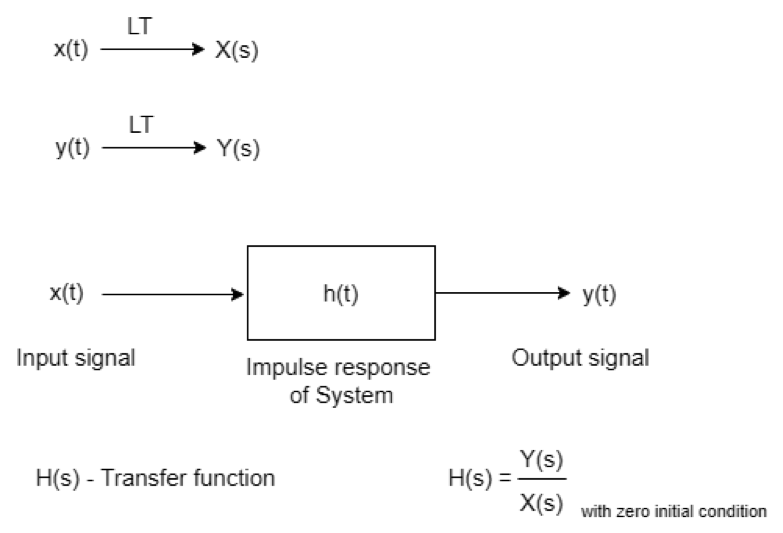
La función de transferencia es la relación entre la transformada de Laplace de la salida y la transformada de Laplace de la entrada cuando se supone que todas las condiciones iniciales son cero. La función de transferencia no se puede definir si no se supone que la condición inicial sea cero.
Las condiciones iniciales cero significan que el sistema debe ser lineal, ya que en la práctica se utilizan sistemas lineales variables en el tiempo.
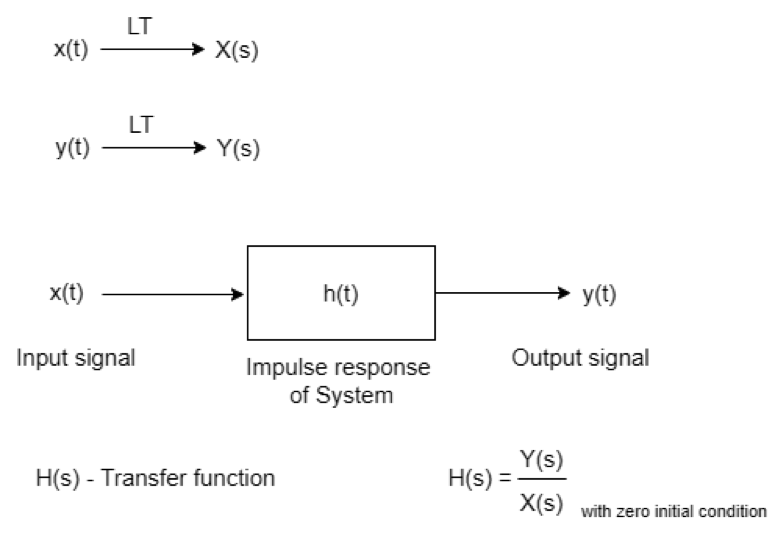
Figura 1 Diagrama de bloques de la función de transferencia.
Debido a la impedancia de un inductor o condensador, los filtros tienen una respuesta dependiente de la frecuencia que cambia con la frecuencia.
Dado que en la práctica se utilizan señales variables en el tiempo y estas señales pasan a través de un circuito (filtrado, amplificación, atenuación), existe la posibilidad de que estas señales se vean afectadas por los componentes (inductor, condensador y resistencias) utilizados en el circuito. Y los filtros se utilizan para atenuar una parte de la frecuencia de la señal.
Como sabemos, w las impedancias de un capacitor y una inducción, respectivamente, son
Zc = 1/sC
Z i = sL
Plano S s = ó +jù
El plano S es un plano complejo (que tiene componentes reales e imaginarios) en matemáticas en el que se puede trazar la transformada de Laplace.
Donde frecuencia neper, nepers por segundo (NP/s)
ù frecuencia angular (rad/s)
La función de transferencia del filtro se puede desarrollar utilizando técnicas de análisis de circuitos estándar. Estas técnicas son las leyes de tensión y corriente de Kirchoff, la ley de Ohm y la superposición. Como sabemos que las impedancias son complejas, la función de transferencia será
H(s) = I es I + a m-1 es m-1 +…+ a 1 s + a 0 b n es n +b n-1 es n-1 +…+b 1 s + b 0
Donde m es el grado del numerador, n es el grado del denominador y H(s) es la función racional de s.
El grado del denominador se llama orden del filtro. Al resolver la ecuación anterior, obtendrás raíces que determinan los ceros (numerador) y los polos (denominador) del circuito de filtro. Cada polo proporciona una respuesta de -6 dB/octava o -20 dB/década y cada cero proporciona una respuesta de +6 dB/octava o +20 dB/década. Las raíces calculadas de la función de transferencia pueden ser reales o complejas. Si son complejas, entonces las raíces se dibujan en el plano s (el plano complejo) donde el eje horizontal es real (ó,) y el eje vertical es el eje imaginario (ù). La distribución de las raíces en el plano s o plano complejo nos dice muchas cosas sobre el circuito del filtro. Para la estabilidad del sistema, todos los polos deben estar en el lado izquierdo del plano complejo. Cero en el origen significa que hay cero en el numerador, lo que significa que el filtro no tendrá respuesta de CC.
Consideremos el circuito RLC y escribamos una función de transferencia para él.

El voltaje a través de la resistencia es
H(s) = VoVin = RCsLCs 2 + RCs +1)
Si R = 10, L = 10 mH, C = 10 uF, entonces se sustituyen los valores de los componentes.
H(s) = 10 3 x(s 2 + 10 3 s + 10 7 )

Después de factorizar,
H(s) = 10 3 x (s(s-(-0.5+j3,122)x10 3 ) x (s-(-0.5-j3,122)x10 3 ))
La ecuación anterior da un cero en el otro origen y polo en:
S = (-0,5±j3,122)x 10 3
El plano anterior muestra estos puntos.
En aplicaciones reales, en la mayoría de los casos, estamos más interesados en el rendimiento del circuito de hardware. Pero también deberíamos fijarnos en el plano s del filtro, Neper y las frecuencias imaginarias.
Frecuencia de corte (F 0 ) y factor de calidad (Q)
Trabajar con un plan S no es tan conveniente, entonces surge la pregunta ¿por qué? La respuesta es: necesita conocer la función de transferencia para comprender el factor de calidad y la frecuencia de corte.
Frecuencia de corte (F 0 )
La frecuencia de corte es la frecuencia a la que el filtro comienza a filtrar la señal, por lo que la frecuencia de corte en un filtro de paso bajo es la frecuencia a la que el filtro comienza a eliminar las frecuencias altas, la frecuencia de corte es en realidad el punto donde el nivel de salida es 3 dB menor que el nivel de entrada, por lo que no es exactamente el punto donde el filtro comienza a funcionar.

La frecuencia de corte es un límite en la respuesta de frecuencia de un sistema; la energía que fluye a través del sistema comienza a reducirse, atenuarse o reflejarse en lugar de atravesarlo. Normalmente, en sistemas electrónicos como filtros y canales de comunicación, la frecuencia de corte se aplica a un borde en las características de paso bajo, paso alto, paso de banda o eliminación de banda de una frecuencia que caracteriza un límite entre la banda de paso y la banda de paso. banda final. A veces se lleva al punto de la respuesta del filtro donde se encuentran la banda de transición y la banda de paso.
La frecuencia de corte generalmente se define como la frecuencia a la que la respuesta del filtro está 3 dB por debajo de la banda de paso. La frecuencia a la que la relación (salida/entrada) tiene una magnitud de 0,707. Si conviertes esta magnitud a decibelios, obtienes -3 dB, lo que significa un punto negativo de 3 dB.
dB = 20 registro (0,707)
La cantidad de atenuación del filtro comienza a aumentar rápidamente en este punto, como se muestra en la siguiente figura.

Factor de calidad (Q)
El factor de calidad es una medida del pico del filtro. En realidad, Q solo es válido para el filtro de segundo orden y no es válido para sistemas de primer o tercer orden. El factor de calidad se define como la caída de potencial a través del inductor o condensador respecto a la caída de potencial a través de la resistencia.
Q = (Caída de tensión en “L”) / (caída de tensión en “R”)
O
Q = (caída de tensión en “C”) / (caída de tensión en “R”)
Cálculo del factor de calidad del inductor:
Q = (I X I ) / (I R)
Q = X L / R = wL / R
Q = 2pfL/R
f es la frecuencia de resonancia, f = 1/2p sqrt (LC)
Q = (1/R) cuadrado(L/C)
De manera similar, también se calcula el factor de calidad de un capacitor, que también es,
Q = (1/R) cuadrado(L/C)
Para un circuito RC, LR o RLC, la función de transferencia será la misma que la ecuación anterior.
El factor de calidad es qué tan subamortiguado está un resonador, es decir, qué tan rápido desaparece una oscilación.
Q es el factor de calidad y la función de transformación del factor de calidad se expresa como
α = 1/Q
Si Q > 0,707, habrá un pico en la respuesta del filtro.
Si Q < 0,707, la tirada en f 0 será mayor.