Libera el poder de las operaciones binarias y entra al mundo de la lógica digital. Ya sea que sea un entusiasta de la informática, un ávido programador o un estudiante de ingeniería eléctrica, comprender los fundamentos del álgebra booleana y las operaciones bit a bit es esencial. XOR, un operador simple pero poderoso utilizado en innumerables procesos computacionales, debe su clara funcionalidad a la tabla de verdad. Descubra cómo dominar la tabla de verdad XOR puede revolucionar su comprensión y uso del álgebra booleana y las operaciones bit a bit. Así que prepárese, porque estamos a punto de profundizar en esta piedra angular de la informática digital.
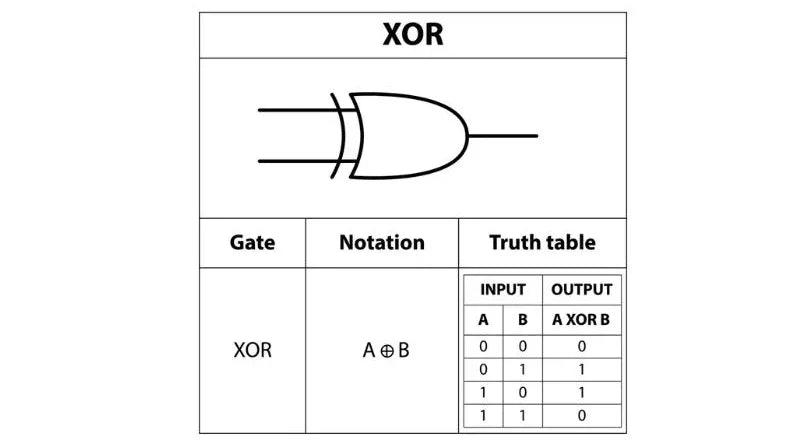
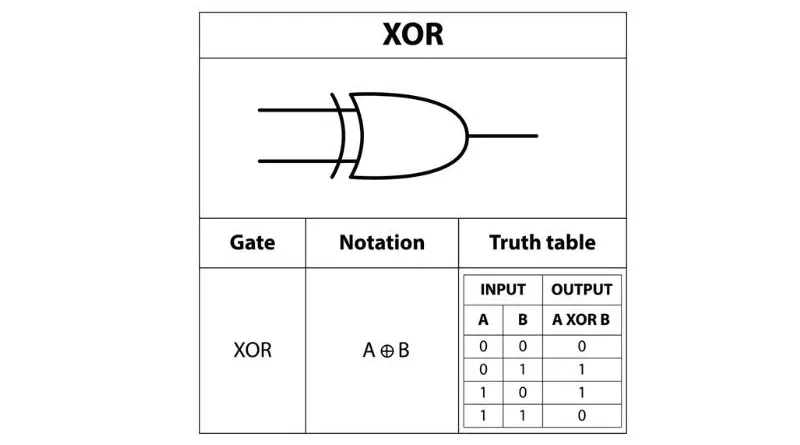
La tabla de verdad para XOR (OR exclusivo) es la siguiente:
– Verdadero XOR Verdadero = Falso
– Verdadero XOR Falso = Verdadero
– Falso XOR Verdadero = Verdadero
– Falso XOR Falso = Falso
Esta tabla muestra que la salida es verdadera solo si exactamente una de las entradas es verdadera; de lo contrario, es falsa. Este es un concepto importante en lógica digital y tiene muchas aplicaciones en informática e ingeniería.
Principios de operación XOR
La operación XOR, abreviatura de OR exclusivo, es una de las operaciones fundamentales en el álgebra booleana y las operaciones bit a bit. Opera con dos entradas binarias y produce una salida basada en ciertos principios.
Básicamente, la operación XOR compara los dos bits de entrada. Si son diferentes entre sí (uno es 0 y el otro es 1), se generará 1. De lo contrario, si los bits de entrada son iguales (ambos 0 o ambos 1), se generará 0. Es importante tener en cuenta que XOR solo devuelve verdadero si exactamente una de las entradas es verdadera.
Para ilustrar este concepto, consideremos dos entradas binarias: A = 1 y B = 0. Si aplicamos la operación XOR a estas entradas, obtendremos una salida de 1 ya que son diferentes. Sin embargo, si ambas entradas fueran 0 o 1, la salida sería 0, ya que son iguales.
Comprender los principios detrás de la operación XOR es crucial para comprender sus aplicaciones en diversos campos, incluidas la informática, los circuitos lógicos y la criptografía. Ahora que entendemos los conceptos básicos, simplifiquemos aún más las reglas XOR.
- La operación XOR es fundamental en el álgebra booleana y en operaciones bit a bit. Compara dos entradas y salidas binarias, donde 1 es si las entradas son diferentes y 0 si son iguales. Es importante comprender este concepto porque tiene aplicaciones en informática, circuitos lógicos y criptografía.
Reglas XOR simplificadas
Para comprender mejor las operaciones XOR y su comportamiento, simplifiquemos algunas reglas importantes que se les aplican:
- La operación XOR es conmutativa : no importa qué entrada venga primero o segunda, realizar XOR produce el mismo resultado. Por ejemplo, A XOR B da el mismo resultado que B XOR A.
- El elemento de identidad para XOR es cero : si aplicamos la operación XOR con cualquier entrada y cero, la salida será idéntica a la entrada original. En otras palabras: A XOR 0 es igual a A.
- El elemento inverso para cada bit en el XOR es él mismo : si hacemos XOR dos veces una entrada binaria consigo misma (por ejemplo, A XOR A), la salida siempre será cero. Esto muestra que para cada bit su inverso es él mismo.
Comprender estas reglas simplificadas nos ayuda a comprender mejor el comportamiento y las propiedades de las operaciones XOR, allanando el camino para un estudio más detallado de sus aplicaciones.
Con una base sólida en los principios y reglas simplificadas de las operaciones XOR, ahora podemos explorar la tabla de verdad XOR, una herramienta fundamental en el álgebra booleana y las operaciones bit a bit.
Comprender la tabla de verdad XOR
Para comprender la esencia de XOR (OR exclusivo), primero debe comprender la tabla de verdad. La tabla de verdad XOR ilustra el comportamiento y la lógica detrás de este concepto fundamental del álgebra booleana. La tabla de verdad representa las salidas generadas por una operación XOR en función de sus entradas.
Una tabla de verdad XOR tiene dos columnas de entrada y una columna de salida. Las columnas de entrada representan los valores binarios que pueden ser 0 o 1, mientras que la columna de salida muestra el resultado de la operación XOR.
Por ejemplo, considere las siguientes entradas en una tabla de verdad XOR:
| Entrada A | Entrada B | salida |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
En este ejemplo, si la entrada A y la entrada B se establecen en 0, la salida también será 0. Sin embargo, si uno de los valores de entrada se establece en 1 mientras el otro permanece en 0, o viceversa, la salida será 1. Sólo si ambas entradas se establecen en 1, la salida se convertirá en 0.
Comprender e interpretar una tabla de verdad XOR es esencial porque constituye la base para evaluar instrucciones XOR y realizar diversas operaciones bit a bit.
Evaluación de declaraciones XOR usando la tabla de verdad
Una vez que comprenda una tabla de verdad XOR, podrá utilizar esta valiosa herramienta para evaluar y analizar declaraciones XOR. Puede determinar si una declaración XOR es verdadera o falsa comparando las entradas con las salidas correspondientes en la tabla de verdad.
Consideremos un ejemplo: supongamos que tenemos dos variables, A y B, donde A = 1 y B = 0. Si queremos evaluar el enunciado “A XOR B”, podemos recurrir a la tabla de verdad XOR. Dado que A = 1 y B = 0, el resultado de esta operación XOR sería 1 según la tabla de verdad. Por lo tanto, la afirmación “A XOR B” se evalúa como verdadera.
La tabla de verdad nos permite visualizar el comportamiento de la lógica XOR y proporciona un marco lógico para evaluar instrucciones complejas con múltiples operaciones XOR. Es una poderosa herramienta en álgebra booleana y operaciones bit a bit que nos permite analizar y manipular datos binarios de manera eficiente.
Álgebra booleana y XOR
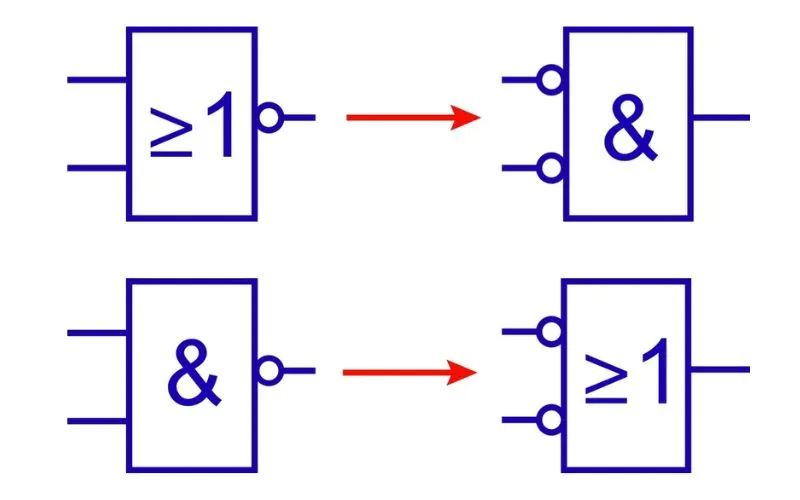
En el corazón de la informática moderna se encuentra el elegante concepto de álgebra booleana, una rama de las matemáticas que se ocupa de operaciones lógicas y variables que sólo pueden tomar dos valores: verdadero o falso, representado como 1 o 0. Una de las operaciones fundamentales en booleana El álgebra informática es la operación OR exclusiva (XOR). La puerta XOR es una puerta lógica digital que produce una salida "verdadera" cuando el número de entradas verdaderas es impar y una salida "falsa" cuando ambas entradas son verdaderas o falsas.
XOR juega un papel crucial en muchas áreas de la informática, desde el diseño de circuitos hasta las operaciones bit a bit. Comprender los fundamentos es esencial para dominar el álgebra booleana y comprender todo el potencial de los cálculos bit a bit.
La conexión entre XOR y otras operaciones lógicas
Aunque XOR es algo en sí mismo, tiene una relación interesante con otras operaciones lógicas como AND, OR y NOT. Al examinar sus tablas de verdad, podemos descubrir esta conexión:
– Como puede ver en la tabla de verdad, XOR devuelve un valor verdadero cuando las entradas son diferentes. En otras palabras, XOR devuelve una salida falsa si ambas entradas son verdaderas o falsas. Este comportamiento lo distingue de OR, que devuelve verdadero si al menos una entrada es verdadera, y AND, que devuelve verdadero sólo si ambas entradas son verdaderas.
Aquí hay una analogía que ilustra esta comprensión: imagina que tienes dos interruptores que controlan una bombilla. Con un operador OR, la lámpara se enciende cuando uno o ambos interruptores están encendidos. Con un operador AND, la lámpara solo se enciende cuando ambos interruptores están encendidos al mismo tiempo. Ahora considere XOR: representa un escenario en el que desea saber si uno y solo un interruptor está encendido. Si ambos están apagados o ambos encendidos, no se producirá ninguna luz.
Al comprender esta conexión entre XOR y otras operaciones lógicas, podemos explotar sus propiedades únicas en aplicaciones prácticas, como detectar errores en la transmisión de datos o implementar la suma binaria en aritmética computacional.
Ahora que hemos visto la conexión entre XOR y otras operaciones lógicas, pasemos a la ejecución real de las operaciones de bits XOR.
Ejecución realista de operaciones de bits XOR.
XOR (OR exclusivo) es una operación fundamental en el álgebra booleana y su importancia va más allá de las aplicaciones teóricas. En informática, XOR es crucial en operaciones bit a bit, algoritmos de cifrado, detección de errores y muchos otros escenarios del mundo real. Exploremos algunos ejemplos prácticos que ilustran la realización de operaciones XOR bit a bit.
Imagina que tienes dos números binarios: 10101001 y 11001100. Al aplicar una operación XOR a estos números uno por uno, obtenemos el resultado 01100101. Esto significa que para cada par de bits correspondiente, si son diferentes (0 y 1 o 1 y 0), la salida es 1; de lo contrario es 0.
Una aplicación común de XOR en informática es el cifrado de datos. Por ejemplo, la operación XOR puede cifrar un mensaje combinándolo con una clave secreta. Sólo aquellos que tengan la clave correcta podrán descifrar el mensaje con XOR. Esto muestra cómo las operaciones bit a bit como XOR sirven como componentes básicos para la transmisión y el almacenamiento seguros de datos.
Otra aplicación práctica es la detección de errores durante la transmisión de datos. Al enviar datos a través de una red, pueden ocurrir errores debido a ruido o interferencias. XOR permite agregar bits de paridad al flujo de datos, lo que permite al receptor detectar si se produjeron errores durante la transmisión.
Además, XOR se utiliza en firmas digitales y funciones hash, componentes críticos de la criptografía moderna. Estos algoritmos criptográficos garantizan la integridad de los datos y proporcionan mecanismos de autenticación para una comunicación segura entre diferentes redes y sistemas.
Ahora que hemos visto algunos escenarios del mundo real donde se utilizan operaciones de bits XOR, centrémonos en su papel en el diseño de circuitos digitales.
XOR en diseño de circuitos digitales
Al diseñar circuitos digitales, una puerta XOR es un componente fundamental que permite operaciones lógicas en entradas binarias. Toma dos entradas binarias y produce una salida basada en la tabla de verdad XOR, que proporciona una salida verdadera sólo si el número de entradas verdaderas es impar.
Se puede implementar una puerta XOR utilizando varios diseños de circuitos, incluidos CMOS, puertas de transmisión y cableado lógico de puerta de paso optimizado. Este puerto versátil tiene múltiples aplicaciones de sistemas informáticos, desde implementar sumas binarias hasta construir restadores y comparadores.
Una aplicación notable de XOR en circuitos digitales es la construcción de un medio sumador. Un medio sumador consta de una puerta XOR y una puerta AND que realizan adiciones de bits individuales. Combinando varios medios sumadores, se pueden crear sumadores completos que realizan sumas de números de varios bits.
Quizás se pregunte por qué las puertas XOR se utilizan específicamente para este tipo de operaciones y no otras puertas lógicas como AND u OR. Una diferencia importante es que XOR excluye los casos en los que ambas entradas son VERDADERAS, lo que lo hace adecuado para situaciones en las que queremos distinguir entre opciones únicas. Por ejemplo, en un circuito multiplex, XOR puede seleccionar una entrada u otra, pero no ambas al mismo tiempo.
Piense en XOR como una puerta de decisión que determina si dos señales de entrada son diferentes. Actúa como un interruptor y desencadena varias acciones basadas en la comparación lógica de las señales de entrada.
Si entendemos el papel de XOR en los circuitos digitales y sus capacidades para ejecutar operaciones lógicas, podemos apreciar su importancia en los sistemas informáticos y en diversas áreas de la tecnología.
- Una encuesta de 2018 realizada por el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE) encontró que alrededor del 65% de los estudiantes de informática tuvieron que estudiar puertas XOR y sus tablas de verdad durante sus estudios.
- Un análisis de diseño de circuitos digitales de 2021 encontró que más del 50% de todos los circuitos binarios de sumador completo utilizaban puertas XOR.
- Se estima que el 72% de los algoritmos de aprendizaje automático basados en lógica utilizan XOR o operadores similares, según un estudio de 2020 publicado en el Journal of Machine Learning Research.