Convertidores de códigos de construcción que utilizan circuitos integrados de la serie SN-7400 - DE Parte 12

En el primer tutorial de esta serie, Introducción a la electrónica digital, se mencionó que existen diferentes sistemas de códigos que se utilizan para representar información digital como números binarios. Cada sistema de código tiene diferentes números binarios asignados a los mismos símbolos y caracteres. Diferentes sistemas digitales pueden utilizar diferentes sistemas de códigos. En este caso, deben quedar algunos circuitos de conversión de código para que los sistemas digitales interconectados sean compatibles.

En este tutorial, se diseñarán circuitos de conversión de código utilizando la serie SN7400 de circuitos integrados digitales. En el tutorial anterior, se utilizó la misma serie de circuitos integrados digitales para construir circuitos aritméticos como medio sumador, medio sumador, medio restador y restador completo. En este tutorial, se diseñarán los siguientes circuitos de conversión de código:

· Conversor de código binario a Gray

· Convertidor de código Gray a binario

· Exceso de BCD – Conversor de 3 códigos

· Exceso – código 3 al convertidor BCD

Los circuitos de conversión de códigos diseñados en este tutorial se utilizarán para convertir los dígitos del 0 al 9 de un sistema de códigos a otro. Los diferentes sistemas de códigos tienen diferentes números binarios asignados a los dígitos. Al igual que en el código gris, los números binarios se ordenan de manera que dos dígitos o valores sucesivos difieran solo en un bit. El sistema de numeración BCD es similar a la representación binaria de números decimales, excepto que el número codificado se separa en cuatro bits para cada dígito del número decimal. Por lo tanto, el número codificado está representado por valores binarios ponderados donde cada valor tiene 4 bits de longitud y es una representación directa de los dígitos del número decimal. El código Excess-3 es similar al sistema de numeración BCD, con la única diferencia de que cada valor de 4 bits de longitud en el número codificado se obtiene sumando 3 a la representación BCD. La siguiente tabla resume la representación binaria de los dígitos del 0 al 9 en diferentes sistemas de código:

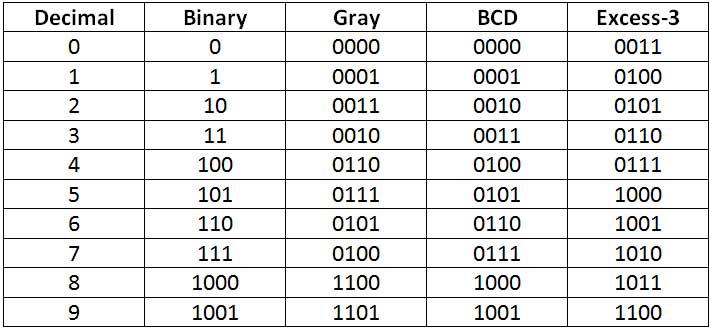
Fig. 1: Tabla que enumera la codificación binaria, gris, BCD y Express-3 para dígitos decimales

Con el conocimiento de estos sistemas de código, comencemos ahora a construir los circuitos convertidores de código.

Componentes necesarios –

Fig. 2: Lista de componentes necesarios para fabricar convertidores de código basados ​​en IC de la serie SN-7400

Diagramas de circuitos –

El convertidor de código binario a Gray tiene el siguiente diagrama de circuito:

Fig. 3: Diagrama de circuito del convertidor de código binario a Gray

El convertidor de código gris a binario tiene el siguiente diagrama de circuito:

Fig. 4: Diagrama del circuito del convertidor de código Gray a binario

El convertidor de BCD a código sobrante – 3 tiene el siguiente diagrama de circuito –

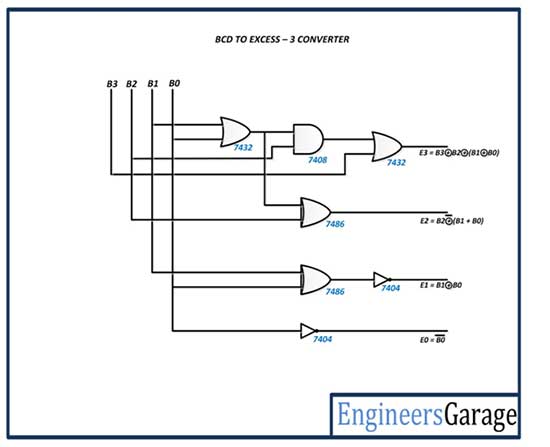
Fig. 5: Diagrama del circuito del convertidor BCD a Exceso 3

El convertidor de código Excess – 3 a BCD tiene el siguiente diagrama de circuito:

Fig. 6: Circuito combinacional del convertidor de código 3 en exceso a BCD

Conexiones de circuito –

Los circuitos convertidores de código diseñados en este tutorial son circuitos combinacionales ya que su salida depende únicamente de los valores de entrada actuales. Cada circuito tiene una tabla de verdad única de la cual se puede derivar la expresión booleana respectiva para cada salida. La expresión booleana minimizada se convierte luego en un diagrama de puerta lógica que se construye en una placa utilizando circuitos integrados de la serie 7400.

Los siguientes circuitos integrados de puerta lógica se utilizan en la construcción de los circuitos:

7408 IC: el 7408 IC tiene puertas AND cuádruples de 2 entradas. El IC tiene la siguiente configuración de pines:

Fig. 7: Diagrama de circuito del convertidor excedente 3 a código BCD

El IC tiene el siguiente diagrama de pines:

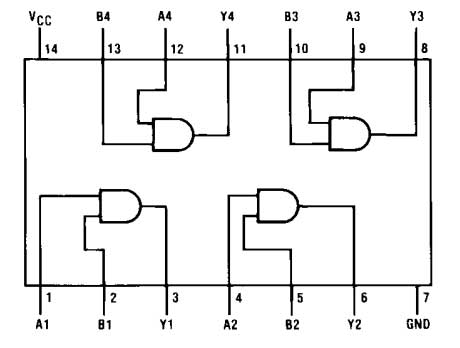
Fig. 8: Diagrama de pines del 7408 IC

El IC requiere una tensión de alimentación de 5 V que puede tolerarse hasta 7 V. El voltaje en las entradas de la puerta AND debe ser de 2 V para lógica alta y de 0 V para lógica baja. La salida de las compuertas AND tiene un voltaje de 3,4 V para lógica alta y 0,2 V para lógica baja. El CI opera en un sistema de lógica positiva. El retardo de propagación durante el tránsito de BAJO a ALTO en la salida es de 27 ns, mientras que el retardo de propagación durante el tránsito de ALTO a BAJO en la salida es de 19 ns.

7432 IC: el 7432 IC tiene puertas OR cuádruples de 2 entradas. El IC tiene la siguiente configuración de pines:

Fig. 9: Tabla que enumera la configuración de pines del 7432 IC

El IC tiene el siguiente diagrama de pines:

Fig. 10: Diagrama de pines del 7432 IC

El IC requiere una tensión de alimentación de 5 V que puede tolerarse hasta 7 V. El voltaje en las entradas de las puertas OR debe ser de 2 V para lógica alta y de 0 V para lógica baja. La salida de las puertas OR tiene un voltaje de 3,4 V para lógica alta y 0,35 V para lógica baja. El CI opera en un sistema de lógica positiva. El retardo de propagación durante el tránsito de BAJO a ALTO en la salida es de 3 a 15 ns, mientras que el retardo de propagación durante el tránsito de ALTO a BAJO en la salida también es de 3 a 15 ns.

7486 IC : el 7486 IC tiene puertas EX-OR cuádruples de 2 entradas. El IC tiene la siguiente configuración de pines:

Fig. 11: Tabla que enumera la configuración de pines del 7486 IC

El IC tiene el siguiente diagrama de pines:

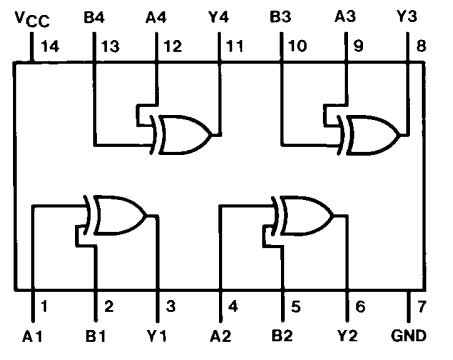
Fig. 12: Diagrama de pines del 7486 IC

El IC requiere una tensión de alimentación de 5 V que puede tolerarse hasta 7 V. El voltaje en las entradas de las compuertas EX-OR debe ser de 2 V para lógica alta y de 0 V para lógica baja. La salida de las compuertas EX-OR tiene un voltaje de 3,4 V para lógica alta y 0,2 V para lógica baja. El CI opera en un sistema de lógica positiva. El retraso de propagación durante la transición de LOW a HI en la salida es de 23 ns si otras entradas son bajas y de 30 ns si otras entradas son altas, mientras que el retraso de propagación durante la transición de HI a LOW en la salida es de 17 ns si otras entradas son bajos y 22 ns si otras entradas son altas.

7404 IC : el 7404 IC tiene seis puertos de inversor. El IC tiene la siguiente configuración de pines:

Fig. 13: Tabla que enumera la configuración de pines del 7404 IC

El IC tiene el siguiente diagrama de pines:

Fig. 14: Diagrama de pines del 7404 IC

El IC requiere una tensión de alimentación de 5 V que puede tolerarse hasta 7 V. El voltaje en las entradas de las puertas NOT debe ser de 2 V para lógica alta y de 0,8 V para lógica baja. La salida de las puertas NOT tendrá un voltaje de 3,4 V para lógica alta y 0,2 V para lógica baja. El IC opera en un sistema de lógica positiva. El retardo de propagación durante el tránsito del nivel BAJO al ALTO en la salida es de 22 ns, mientras que el retardo de propagación durante el tránsito del nivel ALTO al BAJO en la salida es de 15 ns.

Cabe señalar que los circuitos integrados seleccionados tienen niveles de voltaje de entrada, salida y potencia compatibles, ya que provienen de una familia común (serie 74XX) de circuitos integrados digitales.

Cómo funciona el circuito –

Existen diferentes sistemas de códigos disponibles para representar información digital. Los sistemas digitales suelen utilizar componentes que pueden utilizar diferentes sistemas de código. En este caso, debe existir algún circuito convertidor de código entre dichos componentes, para que puedan comunicar información digital entre ellos. Los sistemas de código más utilizados incluyen código Gray, BCD y Excess-3. En todos estos sistemas de código, cada dígito binario está representado por un valor único de 4 bits. Por conveniencia, la entrada binaria al convertidor de código binario a gris y la salida binaria al convertidor de código gris a binario también tienen una longitud de 4 bits.

Así, dado que cada código utiliza cuatro bits para representar un dígito decimal, hay cuatro entradas y cuatro salidas. Cabe señalar que el código Gray es un código no ponderado, mientras que BCD y Excess-3 son sistemas de código ponderado. En los convertidores de código BCD y Excess-3, el circuito está diseñado para conversión de un solo dígito únicamente. Las variables de entrada se designan como B3, B2, B1, B0 y las variables de salida se designan como G3, G2, G1, G0. A partir de la tabla de verdad, se obtienen los mapas K para cada una de las cuatro salidas de los circuitos respectivos y se derivan funciones booleanas que involucran cuatro variables de entrada para cada variable de salida. Se obtiene un diagrama lógico de dos niveles directamente a partir de las expresiones booleanas derivadas de los mapas y se diseñan circuitos combinacionales para cada variable en los respectivos circuitos.

Convertidor de código binario a Gray –

Los números binarios son representaciones no ponderadas de números decimales en base 2. El código Gray, que también se llama código binario reflejado (RBC) o simplemente binario reflejado (RB), tiene números binarios ordenados hasta los dígitos decimales de tal manera que dos valores sucesivos difieren sólo en un bit. El código Gray se utiliza ampliamente en sistemas de comunicación digitales para la corrección de errores. Los números binarios de entrada aquí se consideran de 4 bits de longitud. Para derivar el código gris equivalente a los números binarios, primero se anota el MSB (bit más significativo) tal como está, luego cada dígito inferior en el número del código gris se obtiene sumando el bit respectivo y el bit una posición más abajo en el número binario. El circuito tiene cuatro entradas ( B3 B2 B1 B0) que representan números binarios de 4 bits y cuatro salidas (G3 G2 G1 G0) que representan código Gray de 4 bits. El circuito convertidor tiene la siguiente tabla de verdad:

Fig. 15: Tabla de verdad del convertidor de código binario a Gray

De la tabla de verdad anterior, se obtienen los siguientes K-Maps para las variables de salida:

Fig. 16: K-Map para G3 en conversor de código binario a código Gray

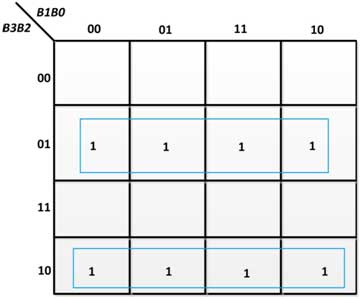
Fig. 17: K-Map para G2 en conversor de código binario a código Gray

Fig. 18: K-Map para G1 en convertidor de código binario a código Gray

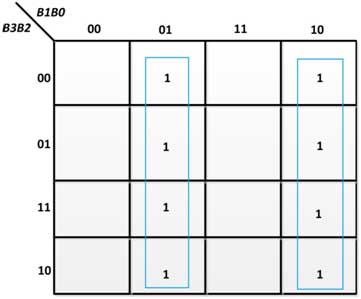
Fig. 19: K-Map para G0 en conversor de código binario a código Gray

De los K-maps anteriores, se obtienen las siguientes expresiones booleanas para las variables de salida:

G3 = B3

G2 = B3 B2

G1 = B2 B1

G0 = B1 B0

Por lo tanto, el circuito digital convertidor de código binario a código Gray utiliza puertas EX-OR. Se puede construir utilizando 7486 IC.

Convertidor de código Gray a binario

Para la conversión de código Gray a binario, el MSB se escribe tal cual y los bits subsiguientes se obtienen sumando MSB (o bit de posición alta en el número binario convertido) y el bit respectivo en el número codificado en Gray. El circuito tiene cuatro entradas (G3 G2 G1 G0) que representan código Gray de 4 bits y cuatro salidas (B3 B2 B1 B0) que representan números binarios de 4 bits. El circuito convertidor tiene la siguiente tabla de verdad:

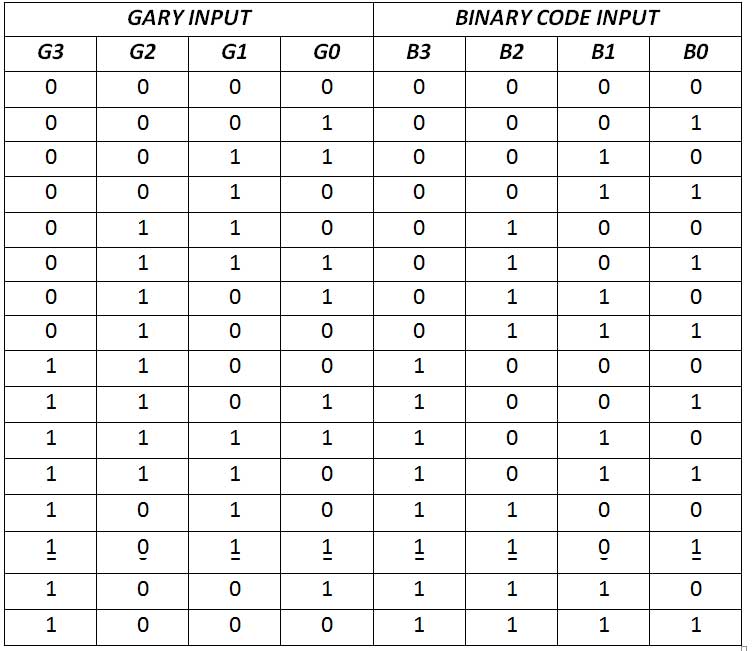
Fig. 20: Tabla de verdad del convertidor de código Gray a binario

De la tabla de verdad anterior, se obtienen los siguientes K-Maps para las variables de salida:

Fig. 21: K-Map para B3 en código gris al convertidor binario

Figura 22: K-Map para B2 en código Gray al convertidor binario

Figura 23: K-Map para B1 en código gris al convertidor binario

Figura 24: Convertidor de K-Map a B0 en código Gray a binario

De los K-maps anteriores, se obtienen las siguientes expresiones booleanas para las variables de salida:

B3 = G3

B2 = G3 G2

B1 = G3 G2 G1

B0 = G3 G2 G1 G0

Por lo tanto, el circuito digital convertidor de código gris a binario utiliza puertas EX-OR. Se puede construir utilizando 7486 IC.

Convertidor de BCD a Exceso-3

Los números BCD de 4 bits son iguales a los números binarios de 4 bits. Los números codificados superiores a 3 se suman 3 a cada número BCD. Tanto BCD como Excess-3 son sistemas de código ponderado. El circuito diseñado aquí convierte solo números BCD de un solo dígito en números equivalentes de Exceso-3 de un solo dígito. El circuito tiene cuatro entradas (B3 B2 B1 B0) que representan un código BCD de 4 bits y cuatro salidas (E3 E2 E1 E0) que representan un exceso de 4 bits: 3 números. El circuito convertidor tiene la siguiente tabla de verdad:

Fig. 25: Tabla de verdad del convertidor de BCD a Exceso-3

De la tabla de verdad anterior, se obtienen los siguientes K-Maps para las variables de salida:

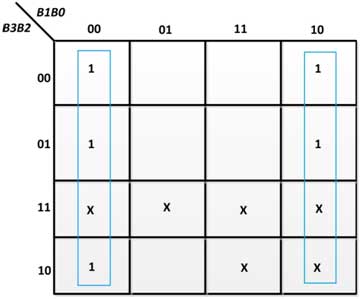
Figura 26: Convertidor de código K-Map para E0 en BCD a Excess-3

Figura 27: Convertidor de código K-Map para E1 en BCD a Excess-3

Figura 28: Convertidor de código K-Map para E2 en BCD a Excess-3

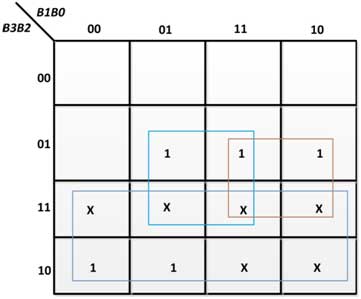
Figura 29: Convertidor de código K-Map a E3 en BCD a Excess-3

De los K-maps anteriores, se obtienen las siguientes expresiones booleanas para las variables de salida:

E0 = B0'

E1=B1 B0

E2 = B2 (B1+B0)

E3 = B3 B2 (B1 B0)

Por lo tanto, el circuito digital convertidor de código BCD a 3 en exceso utiliza puertas EX-OR, AND y NOT. Se puede construir utilizando los IC 7486, 7432, 7408 y 7404.

Convertidor Exceso-3 a BCD

Los números codificados en BCD son tres menos que los números codificados en Exceso-3. El circuito convertidor tiene cuatro entradas (X3 X2 X1 X0) que representan un exceso de 4 bits: 3 códigos y cuatro salidas (ABCD) que representan números BCD de 4 bits. Existe la siguiente tabla de verdad:

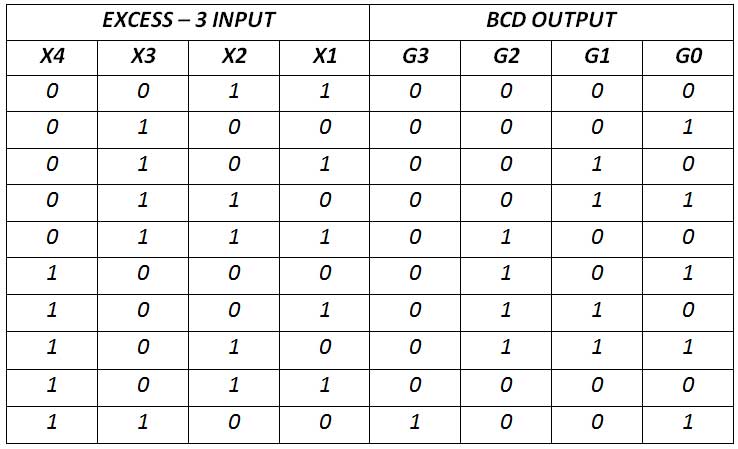
Fig. 30: Tabla de verdad del convertidor Exceso-3 para código BCD

De la tabla de verdad anterior, se obtienen los siguientes K-Maps para las variables de salida:

Figura 31: Convertidor de código K-Map a A en exceso-3 a BCD

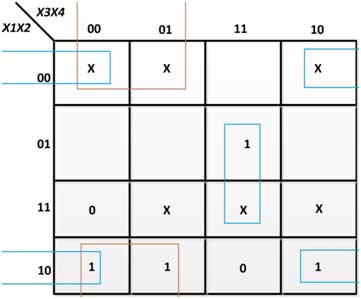
Figura 32 : Convertidor de K-Map para exceso de B-3 a código BCD

Figura 33 : Convertidor de código K-Map a C en exceso-3 a BCD

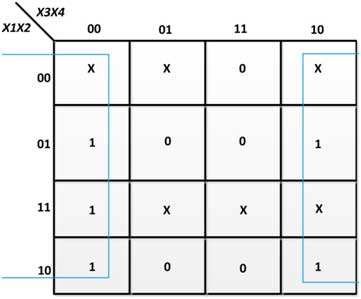
Figura 34 : Convertidor de K-Map a exceso de D-3 a código BCD

De los K-maps anteriores, se obtienen las siguientes expresiones booleanas para las variables de salida:

A = X1(X2 + X3.X4)

B = X2 (X3′ + X4′)

C=X3 X4

D = X4′

Por lo tanto, el circuito digital para el convertidor de código excedente a BCD utiliza puertas EX-OR, AND y NOT. Se puede construir utilizando los IC 7486, 7432, 7408 y 7404.

Probando los circuitos –

Los circuitos diseñados anteriormente se pueden probar suministrando voltaje de suministro a los circuitos integrados mediante una batería a través del regulador de voltaje 7805. El mismo voltaje se puede reducir a un nivel de 2 V usando una resistencia variable para lógica ALTA mientras se suministra lógica BAJA a través de tierra. Las señales de salida se pueden verificar conectando LED a los pines de salida de cada circuito convertidor. Los circuitos se pueden verificar consultando las tablas de verdad de cada circuito.

En el siguiente tutorial, aprenderá a diseñar un comparador de magnitud de bits.

Diagramas de circuito