En el tutorial anterior, se analizaron varias puertas lógicas y su construcción. En el tutorial – Operaciones lógicas booleanas, se analizó cómo, al realizar operaciones lógicas con datos binarios, se pueden realizar operaciones aritméticas. En un circuito digital, muchas puertas lógicas están interconectadas junto con registros y elementos de memoria para realizar una tarea computacional compleja. Cualquier problema computacional se puede expresar como una función booleana o una expresión booleana.
Una expresión booleana toma en consideración las variables booleanas (que pueden verse como fuentes de datos binarios individuales) y representa la relación matemática (en forma de suma y multiplicación) entre ellas. Las operaciones matemáticas como la división y la resta se realizan mediante la multiplicación y la suma. De manera similar, la resta se puede implementar sumando con el complemento y la división se puede implementar multiplicando el divisor por un factor y restando.
Las funciones o expresiones booleanas siguen un conjunto de reglas matemáticas que colectivamente se denominan álgebra booleana. Los diversos teoremas del álgebra booleana son útiles para minimizar una función booleana. Para diseñar un circuito digital optimizado (número mínimo de puertas lógicas para resolver un problema computacional específico), se debe minimizar una expresión booleana. Entonces, comencemos con los teoremas y postulados básicos del álgebra de Boole.
Postulados de Huntington –
El álgebra booleana fue desarrollada por George Boole en el año 1854. En 1904, EV Huntington formuló varios postulados que deben ser satisfechos por un sistema algebraico booleano. Estos postulados son los siguientes:
1) Cierre : si una expresión booleana involucra ciertas variables que pertenecen a un conjunto, digamos S, entonces el conjunto S está cerrado con respecto a un operador binario si para cada par de elementos de S, el operador binario especifica reglas para obtener un elemento único. de S. En otras palabras, si una función booleana involucra ciertas variables booleanas, entonces las variables, así como el resultado de la expresión booleana, deben pertenecer a un conjunto común de elementos. Cualquier expresión booleana siempre sigue el cierre con respecto a la suma binaria (operador +) y la multiplicación binaria (operador .).
2) Identidad : se dice que un conjunto tiene un elemento de identidad para un operador (como *) si existe un elemento, digamos e en el conjunto, tal que e pertenece al conjunto y la multiplicación de e con cualquier otro elemento da como resultado el mismo elemento, es decir, si x también pertenece al mismo definido, entonces x*e = e*x = x. En un sistema booleano, el elemento identidad con respecto a la suma binaria es 0, como para cualquier variable booleana, digamos x, x + 0 = 0 + x = x. De manera similar, el elemento identidad en relación con la multiplicación binaria es 1, como para cualquier variable booleana, digamos x, x.1 = 1.x = x.
3) Conmutativa : cualquier expresión booleana es conmutativa con respecto a la suma binaria y a la multiplicación binaria. Como si hubiera dos variables booleanas: x y u , entonces x + y = y + x. Asimismo, xy = yx
4) Asociativo : cualquier expresión booleana también es asociativa con respecto a la suma binaria y a la multiplicación binaria. Como si hubiera tres variables booleanas: x, y y z, entonces x + (y + z) = (x + y) + z. De manera similar, x.(yz) = (xy).z.
5) Distributiva : en álgebra booleana, la suma binaria es distributiva sobre la multiplicación binaria y la multiplicación binaria es distributiva sobre la suma binaria. Entonces, si hay tres variables booleanas: x, y y z, entonces x.(y + z) = (xy) + (xz). Asimismo, x+(yz) = (x+y). (x+z).
6) Inverso : el álgebra booleana no tiene inverso aditivo ni multiplicativo, ya que no hay operaciones de resta ni división en el álgebra booleana. Sin embargo, cualquier elemento booleano, digamos x, tiene un complemento x' tal que x + x' = 1 y xx' = 0.
La ley asociativa no es un postulado de Huntington, pero es válida para el álgebra de Boole. También cabe señalar que el álgebra de Boole tiene + sobre el operador distributivo. operador. Esto es diferente de las leyes del álgebra ordinaria. También es importante señalar que el álgebra de Boole tiene un complemento, pero no un inverso. El álgebra booleana utilizada en electrónica digital es un álgebra booleana de dos valores. Se define sobre un conjunto, digamos B, que tiene sólo dos elementos – (0, 1). Todos los postulados mencionados anteriormente son válidos en el álgebra booleana de dos valores de la siguiente manera:
1) Cierre : el resultado de cualquier expresión booleana es 0 o 1. Por lo tanto, sigue la ley de cierre en relación con el conjunto (0, 1).
2) Identidad : el 0 es el elemento de identidad en relación con la suma binaria, como para cualquier variable booleana, digamos x, 0 + x = x + 0 = x. Si x = 0, entonces 0 + 0 = 0 + 0 = 0. Si x es 1, entonces 0 + 1 = 1 + 0 = 1. El 1 es el elemento identidad en relación con la multiplicación binaria como para cualquier variable booleana, digamos digamos x, 1.x = x.1 = x. si x = 0, entonces 1,0 = 0,1 = 0. si x = 1, entonces 1,1 = 1,1 = 1.
3) Inverso : el complemento a 0 es 1 y el complemento a 1 es 0. En la suma binaria, 0 + 1 = 1 y en la multiplicación binaria, 0,1 = 0. Para cualquier variable booleana, diga x, x + x' = 1 y xx' = 0 .
Principio de Dualidad –
La dualidad es una propiedad importante del álgebra booleana. Según esta propiedad, cualquier expresión booleana, deducible por los postulados del álgebra booleana (los postulados de Huntington junto con la propiedad asociativa), sigue siendo la misma si se intercambian el operador y los elementos identidad. Por lo tanto, el dual de una expresión booleana se puede obtener intercambiando los operadores Y y O y reemplazando todos los unos con ceros y los ceros con unos.
Teoremas booleanos –
Cualquier expresión booleana es deducible mediante los siguientes teoremas:
Teorema 1: para cualquier variable booleana x, x + x = x y xx = x. Supongamos que si x = 0, entonces 0 + 0 = 0 y 0,0 = 0. Si x = 1, entonces 1 + 1 = 1 y 1,1 = 1.
Teorema 2: para cualquier variable booleana x, x + 1 = 1 y x,0 = 0. Supongamos que, si x = 0, entonces 0 + 1 = 1 y 0,0 = 0. Si x = 1, entonces 1 + 1 = 1 y 1,0 = 0.
Teorema 3 (Involución) – Para cualquier variable booleana x, (x')' = x. Supongamos que x = 0, entonces (0′)' = 1′ = 0. Si x = 1, entonces (1′)' = 0′ = 1.
Teorema 4 (asociativo): para cualquier variable booleana x, y y z, x + (y + z) = (x + y) + z y x. (y.z) = (x.y) . z.
Teorema 5 (Teorema de DeMorgan): este teorema establece la ley de dualidad para el álgebra booleana. Para cualquier variable booleana x e y, (x + y)' = x' . y' y (xy)' = x' + y'.
Teorema 6 (Absorción): para cualquier variable booleana x e y, x + (x. y) = x y x. (x + y) = x. Esto se puede probar de la siguiente manera -
x + (x. y) = (x. 1) + (x. y)
=x(1+y)
=x. 1
=x
Similarmente,
X. (x + y) = (xx) + (xy)
=x + (x.y)
= (x.1) + (x.y)
=x(1+y)
=x. 1
=x
Precedencia de operadores en álgebra booleana –
La precedencia de operadores en orden descendente en álgebra booleana es la siguiente: 1) Paréntesis, 2) NOT, 3) AND y 4) OR. Cualquier expresión booleana se deduce de izquierda a derecha y la prioridad más alta está entre paréntesis. Luego NO, Y y finalmente el operador O.
Función booleana –
Una función booleana es una expresión algebraica booleana que consta de variables booleanas (donde cada variable puede tener un valor de 0 o 1), constantes booleanas (es decir, 0 y 1) y operadores booleanos (como Y, O, NO). Cualquier función booleana prácticamente representa algún cálculo sobre datos binarios. Por ejemplo, supongamos que una función booleana diga que F es como:
F = x + yz
Aquí x, y y z son variables booleanas (fuentes de datos binarios como celdas binarias de un registro) que están relacionadas mediante operadores Y y O en la función anterior. Todos los resultados posibles de una expresión booleana se pueden representar mediante una tabla de verdad. La tabla de verdad enumera todas las combinaciones posibles de los valores de las variables booleanas y las compara con el resultado de la expresión booleana. En cuanto a la función indicada anteriormente , la siguiente es la tabla de verdad:
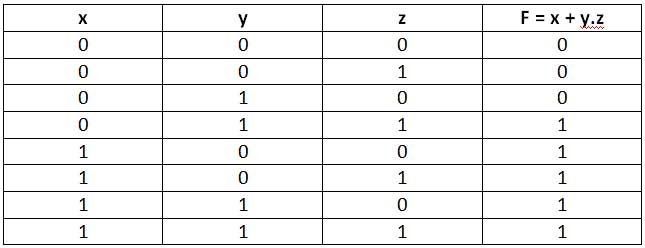
Figura 1: Tabla de verdad para una función booleana
Un circuito digital para la función booleana anterior no es más que la interconexión de puertas lógicas (Y, O, NO) con fuentes de datos binarios (representados por variables booleanas en la función booleana). La multiplicación binaria u operación de puntos entre dos variables equivale a conectar dos fuentes binarias como entrada de la puerta AND. La suma binaria o la operación de suma entre dos variables equivale a conectar dos fuentes binarias como entrada de la puerta OR. El complemento equivale a conectar una fuente binaria a una puerta NOT. Por lo tanto, el circuito digital para la función anterior será el siguiente:
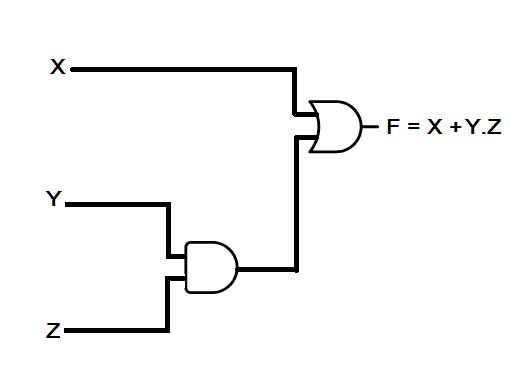
Fig. 2: Imagen que muestra la función booleana convertida en circuito lógico
Complemento de una función booleana –
El complemento de una función booleana se obtiene cambiando todos los ceros por unos y los unos por ceros e intercambiando los operadores Y y O. En una función booleana, reemplazar todos los ceros con unos y todos los unos con ceros se realiza reemplazando las variables booleanas con sus complementos. Por ejemplo, el complemento de la función dada anteriormente será el siguiente:
Si F = x + yz, entonces
F'=x'. (y'+z')
Minterm y Maxterm –
Una variable booleana puede generarse en su forma normal (como x) o en su forma complementaria (como x') en una expresión booleana. Si la operación AND se realiza entre dos variables, digamos x y u , puede haber cuatro combinaciones posibles: xy, x.y', x'.y y x'.y'. Cada uno de estos posibles productos se denomina Minterm o producto estándar. De manera similar, si la operación OR se realiza entre dos variables, digamos x y u , entonces nuevamente hay cuatro combinaciones posibles: x + y, x + y', x' + y y x' + y'. Cada una de estas posibles sumas se denomina Maxterm o sumas estándar.
Para dos variables, x e y, son posibles los siguientes Minterms y Maxterms:
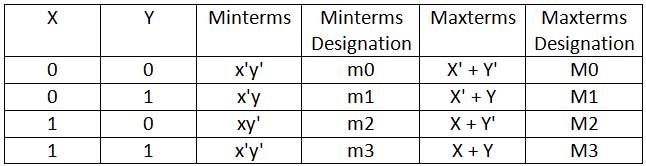
Fig. 3: Tabla que enumera Minterms y Maxterms para dos variables booleanas
De manera similar, para tres variables, digamos x, y y z, son posibles los siguientes Minterms y Maxterms:
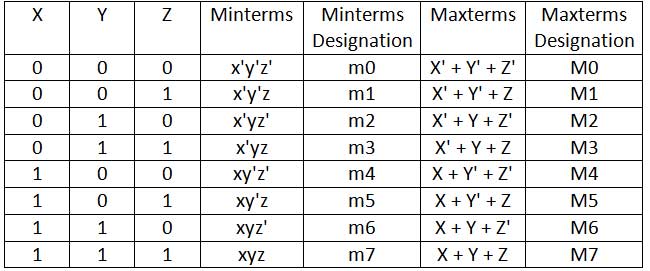
Fig. 4: Tabla que enumera Minterms y Maxterms para tres variables booleanas
Para n variables, puede haber 2^n Minterms y 2^n Maxterms. Cualquier función booleana se puede expresar como la suma de Minterms que producen 1 para la función en la tabla de verdad o Producto de Maxterms que producen 0 para la función en la tabla de verdad, siempre que se conozca la tabla de verdad de la función. Por ejemplo, hay una función F, con la siguiente tabla de verdad. De manera similar, para tres variables, digamos x, y y z, son posibles los siguientes Minterms y Maxterms:
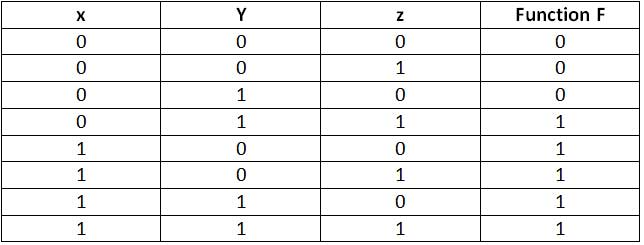
Fig. 5: Tabla de verdad para una función booleana de tres variables
De la tabla de verdad anterior, la función F se puede expresar como la suma de los minitérminos que dan 1 para la función en la tabla de verdad de la siguiente manera:
F = x'yz + xy 'z' + xy'z + xyz ' + xyz = m3 + m4 + m5 + m6 + m7 De la tabla de verdad anterior, la función F se puede expresar como la suma de los minitérminos que dan 1 para la función en la tabla de verdad de la siguiente manera:
De manera similar, se puede expresar como producto de Maxterms que arroja 0 para la función en la tabla de verdad de la siguiente manera:
F = (x' + y' + z') . (x'+y'+z). (x' + y + z') = M0 . M1. M2
Se dice que una función expresada como suma de minterms o producto de maxterms está en su forma canónica. En cuanto a n número de variables, puede haber 2^n minterms y 2^n maxterms, el número de funciones posibles con n número de variables es 2^2n. Entonces, para 2 variables booleanas puede haber 4 minterms y 4 maxterms y el número total de funciones posibles con ellas es 16. Entonces puede haber 16 funciones binarias (operaciones binarias) posibles entre dos variables booleanas o (fuentes binarias).
Cuando se expresa una función en forma de Minterms y Maxterms, puede tener una implementación de dos niveles en puertas lógicas. Siempre se prefiere la implementación de dos niveles, ya que produce la menor cantidad de retraso a través de las puertas cuando la señal se propaga desde la entrada a la salida del circuito digital.
En el próximo tutorial, aprenderá sobre todas las operaciones lógicas posibles entre dos variables booleanas. Hay operaciones lógicas adicionales además de AND, OR y NOT. Todas las operaciones lógicas posibles entre dos fuentes binarias se pueden derivar con conocimiento de funciones y teoremas booleanos.

