1. Preámbulo
Los conos se utilizan ampliamente en combinación y ensamblaje mecánico. Cuando un diseñador especifica el tamaño del cono de un orificio interno y requiere mecanizar un cono externo para que coincida, la tarea puede ser un desafío para los operadores porque el cono externo es difícil de controlar y medir.
En Panzhihua Iron and Steel Co., Ltd., el área principal de la fábrica está equipada con equipos de mecanizado C6120 y CA6140. Al girar un cono con una pequeña placa deslizante, la precisión de deflexión mínima del torno es de 1 grado, lo que dificulta cumplir con los requisitos de alta precisión para mecanizar el cono exterior.
Para cumplir con los requisitos de adaptación, se utilizan otros instrumentos de medición para controlar la conicidad del cono mediante un método de medición relativo.
2. Giro manual de una pequeña placa deslizante cónica corta
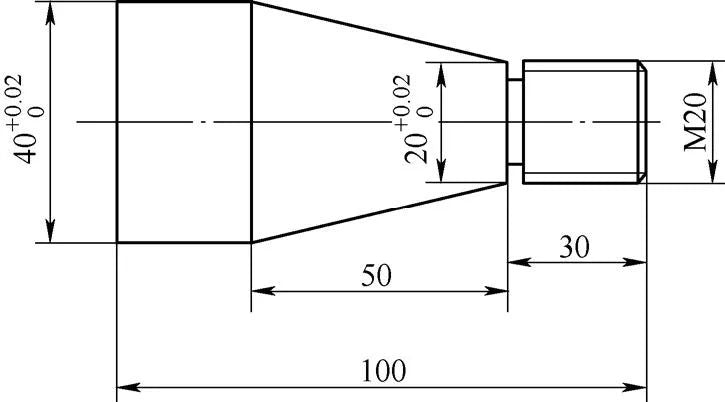
Las piezas que se muestran en la Fig. 1 se componen principalmente de cono y rosca.
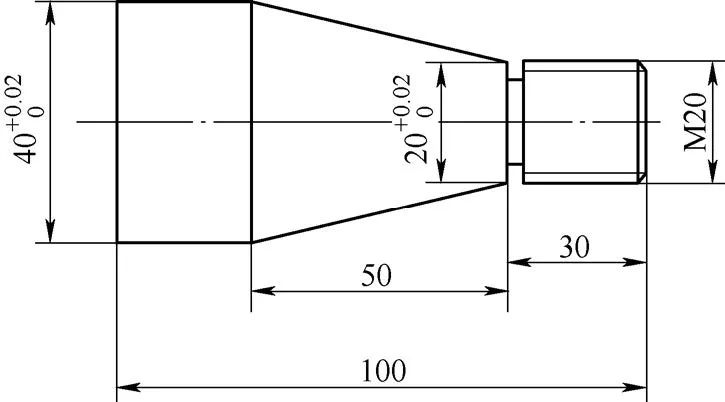
Figura 1 piezas
Las dimensiones del cono están representadas en la Figura 2, consistiendo principalmente en:
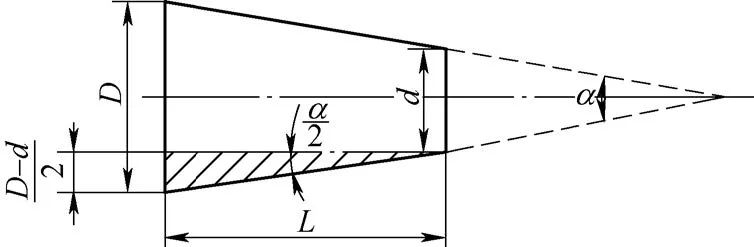
Fig. 2 dimensiones principales de la parte cónica
- Ángulo del cono α, que es el ángulo entre dos líneas radiales.
- Ángulo de medio cono α/2, que es el ángulo de rotación de la placa deslizante más pequeño durante el giro.
- Diámetro máximo del extremo D, comúnmente denominado diámetro del extremo grande.
- Diámetro final mínimo d, comúnmente denominado diámetro final pequeño.
- Longitud del cono L, que es la distancia entre el diámetro del extremo más grande y el diámetro del extremo más pequeño a lo largo del eje.
Al girar un cono, el ángulo de rotación de la placa deslizante más pequeña es α/2, como se ilustra en la Figura 3.
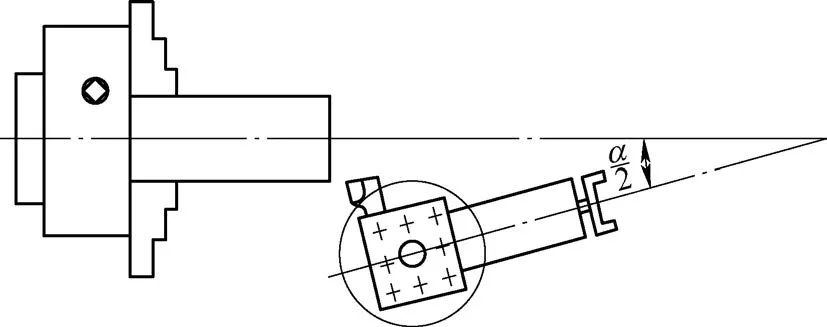
Fig. 3 Diagrama esquemático del ángulo de rotación de la pequeña placa deslizante.
El ángulo de rotación de la placa deslizante más pequeña, α/2, se puede calcular usando la relación de función trigonométrica: tan(α/2) = (D – d)/(2L) = (40 – 20)/(2 x 50 ) = 0,2, lo que da como resultado α/2 = 11°20′.
El ángulo de rotación de la placa deslizante más pequeña es de 11°20′ y su ángulo de rotación se divide en incrementos de 1° sin ninguna subdivisión en 20′. Medir el ángulo con una regla angular universal es un proceso laborioso y que requiere mucho tiempo, y también da como resultado un ángulo cónico inexacto. Esto conduce a una baja precisión de las piezas, lo que dificulta el cumplimiento de los requisitos correspondientes.
Para abordar esta pregunta, se analizó el triángulo rectángulo sombreado en la Figura 2 (ver Figura 4).
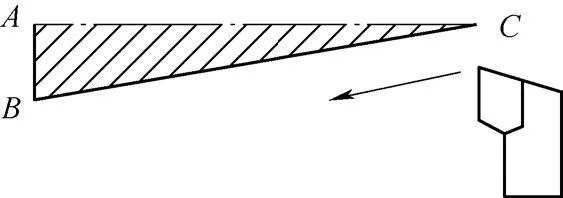
Fig.4 Triángulo rectángulo sombreado
Durante el torneado cónico, la trayectoria de la herramienta de torneado va del punto C al punto B. La longitud de esta trayectoria se puede calcular utilizando el teorema de Pitágoras (consulte la Figura 5).
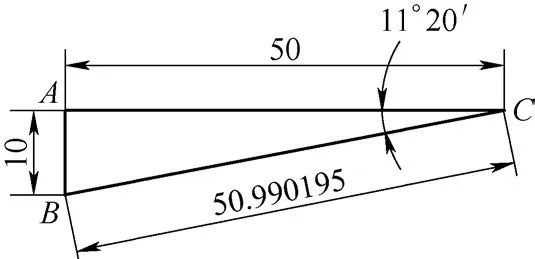
Fig. 5 Longitud de la trayectoria de la herramienta de torneado
Durante el giro, la posición de la punta de la herramienta en relación con los puntos B y C se puede ajustar usando el dial en la pequeña placa deslizante.
Cuando la herramienta se mueve una distancia de 50,99 mm, la distancia entre la punta de la herramienta y el eje del torno debe medir 10 mm, lo que indica que el ángulo del cono de giro es correcto. De lo contrario, el ángulo de rotación de la pequeña placa deslizante será incorrecto.
Se recomienda simular el proceso de mecanizado antes de mecanizar un cono.
Para determinar si el ángulo de rotación de la placa deslizante pequeña es correcto, primero ajuste la placa deslizante pequeña para que la herramienta se mueva una distancia de 50,99 mm y luego use una herramienta de medición para verificar si la distancia entre la punta de la herramienta y el eje del torno es correcta. 10 mm.
Este proceso se puede repetir hasta lograr el ángulo de cono correcto. Los pasos se ilustran en la Figura 6.
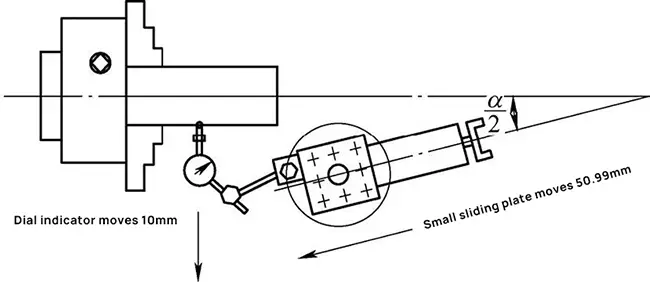
Fig. 6 Diagrama esquemático del método de operación específico.
(1) Comience girando una sección del círculo exterior. La rugosidad de la superficie debe ser baja y no debe haber ningún estrechamiento a lo largo del cilindro.
Para garantizar que no haya conicidad, mida ambos extremos del cilindro con un micrómetro y compare las dimensiones. Si son iguales significa que el cilindro no tiene cono.
(2) Calcule el movimiento del indicador de cuadrante y determine la longitud del lado BC usando el teorema de Pitágoras, que es la distancia exacta que debe recorrer la pequeña placa deslizante cuando el carro es cónico (BC = 50,99 mm).
(3) Gire la placa deslizante pequeña en el sentido contrario a las agujas del reloj de 11° a 12°, asegúrela con un tornillo y luego fije la base del indicador de cuadrante al portaherramientas en la placa deslizante pequeña. Empuje el contacto del indicador de cuadrante dentro del círculo exterior (ver Fig. 6).
(4) Alinee la pequeña placa deslizante con la posición cero y apunte el indicador de cuadrante a la posición de escala de 10 mm. Mueva la pequeña placa deslizante hacia adelante y el contacto del indicador de cuadrante se extenderá gradualmente.
Si la pequeña placa deslizante se mueve 50,99 mm y el indicador de cuadrante se mueve menos de 10 mm, esto indica una pequeña conicidad. En este caso, afloje el tornillo de bloqueo para aumentar la conicidad.
Si la placa deslizante pequeña se mueve 50,99 mm y el indicador de cuadrante se mueve más de 10 mm, esto indica una conicidad grande. Reduzca la conicidad en este caso.
Si la pequeña placa deslizante se mueve 50,99 mm y el indicador de cuadrante se mueve 10 mm, significa que el cono es correcto y el giro puede continuar.
Las precauciones durante el ajuste son las siguientes :
(1) Es importante tener en cuenta que el círculo exterior utilizado para determinar la conicidad no debe tener una conicidad, ya que esto resultará en mediciones inexactas.
Si el círculo exterior girado tiene una forma cónica, alinéelo presionando el indicador de cuadrante contra el manguito del contrapunto.
(2) Para garantizar lecturas precisas, asegúrese de que la base magnética del comparador esté firmemente sujeta y que el tornillo de la biela en el marco del medidor esté apretado sin aflojarse.
(3) La varilla de medición del indicador de cuadrante debe estar perpendicular al eje del círculo exterior. Si es necesario, utilice un cuadrado pequeño para corregir la perpendicularidad y coloque el contacto del indicador de carátula lo más cerca posible del eje del círculo exterior.
(4) Se recomienda utilizar la carrera de medición más larga posible del indicador de cuadrante. Aunque lo habitual es una tira de 10 mm, también se puede preparar una tira de 30 a 50 mm si es necesario.
(5) Este método también se puede aplicar al mecanizado de un cono interno.
3. Torneado automático de herramienta de montura cónica larga
Como se muestra en la Fig. 7, el cono de giro de la alimentación automática de la herramienta de sillín se logra utilizando el método del contrapunto desplazado.
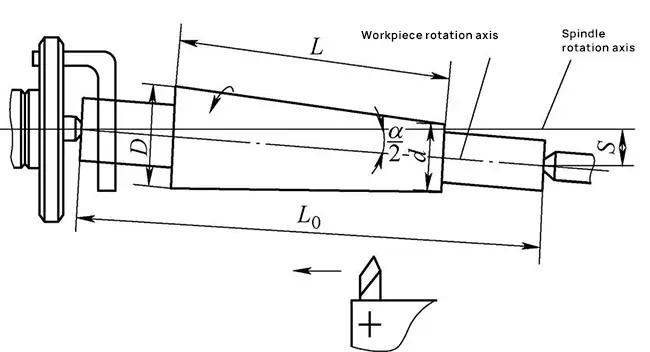
Fig. 7 Torneado cónico con alimentación automática de herramienta de montura
Al mover el contrapunto del torno lateralmente una cierta distancia s, el eje de rotación de la pieza se cruza con el eje del husillo del torno, creando un ángulo incluido igual a la mitad del ángulo del cono de la pieza α/2.
A medida que el soporte base avanza paralelo al eje principal, se produce una conicidad en la pieza de trabajo.
Este método es adecuado para piezas con una pequeña conicidad (menos de 3°) y longitudes largas.
3.1 Cálculo del desplazamiento del contrapunto
Desplazamiento del contrapunto S ≈ L 0 tan( α/ 2) = L 0 (Dd) / (2L) o S = CL 0 / 2, donde,
- S es el desplazamiento del contrapunto (mm);
- D es el diámetro máximo del cono (mm);
- D es el diámetro mínimo del cono (mm);
- L es la longitud del cono (mm);
- l 0 es la longitud total de la pieza (mm);
- C es cónica.
Por exemplo, ao usinar uma peça cilíndrica cônica entre dois centros, com as dimensões fornecidas: D = 80 mm, d = 76 mm, L = 600 mm e L 0 = 1000mm, o deslocamento do contraponto (S) pode ser calculado da seguinte molde:
S = L 0 × (D – d) / (2 × L) = 1000 × (80 – 76) / (2 × 600) = 3,3 mm.
3.2 Medición de compensación del contrapunto
Se debe instalar un indicador de cuadrante en el portaherramientas para medir el desplazamiento del contrapunto, como se muestra en la Fig.
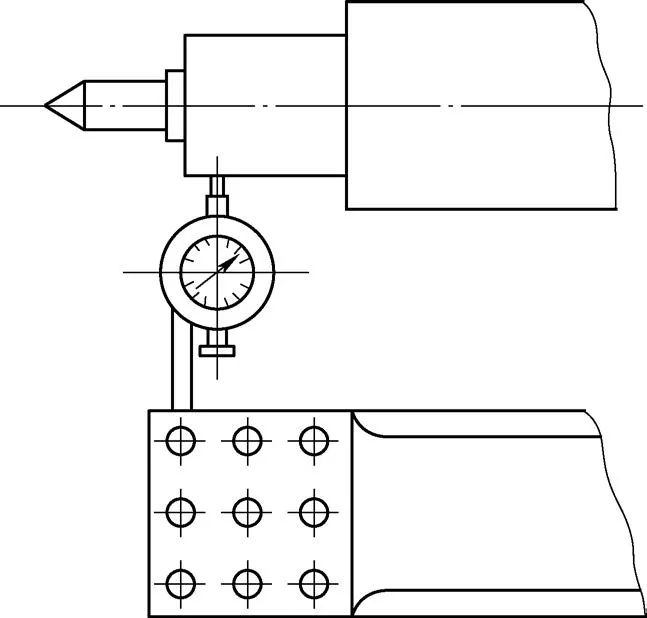
Figura 8 Medición del desplazamiento del contrapunto
3.3 Pasos de giro
La alimentación automática de herramientas desde el soporte base se utiliza para mecanizar una pieza en forma de cono. La pieza de trabajo se sujeta como se muestra en la Fig. 9. El giro aproximado del cono exterior se muestra en la Fig. 9.
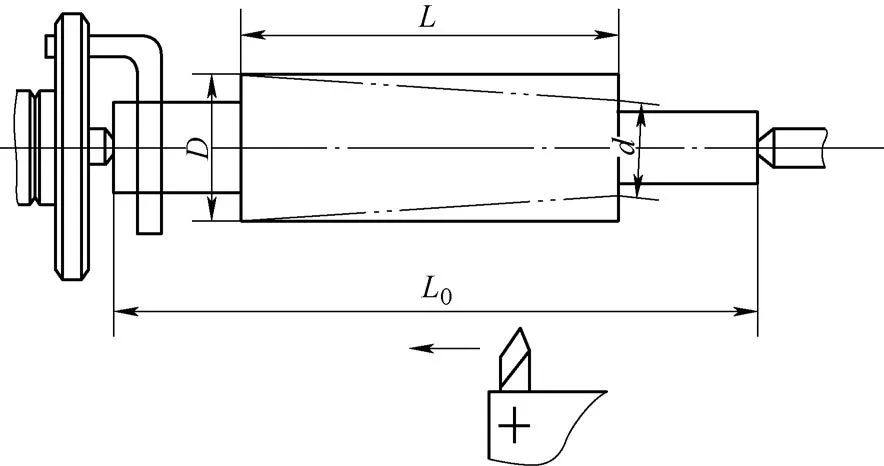
Fig. 9 Sujetar la pieza de trabajo
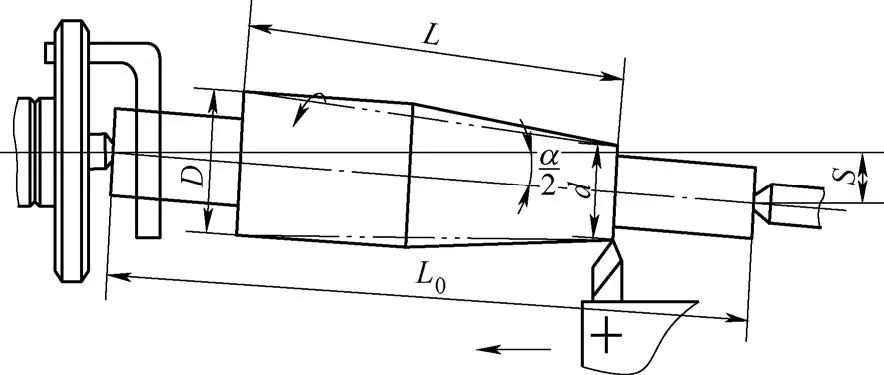
Fig. 10 Cono exterior rugoso
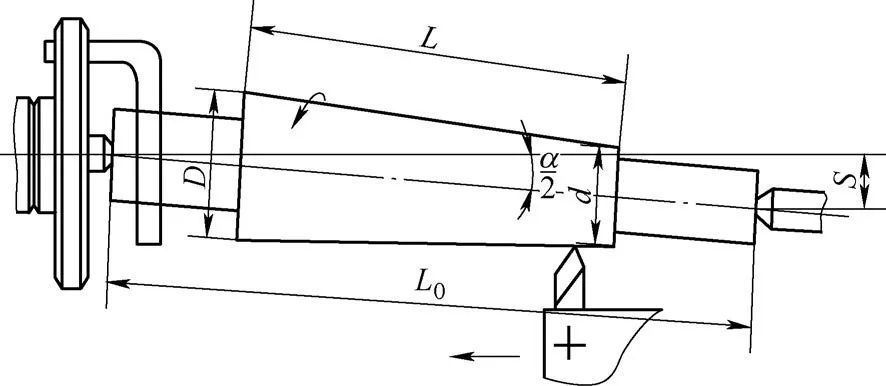
Fig. 11 Completar el giro del cono externo.
Funciones de torneado de cono externo 3.4C con alimentación automática de herramientas de bancada
- Este método es adecuado para mecanizar piezas cónicas externas con un cono pequeño (menos de 3°) y un cono largo. Sin embargo, no se puede utilizar para piezas con una gran conicidad debido a las limitaciones de desplazamiento del contrapunto.
- Al alimentar el soporte base longitudinalmente de forma automática, se reduce la rugosidad de la superficie (Ra) y se mejora la calidad de la superficie de la pieza.
- La punta de la pieza de trabajo puede estar torcida en el orificio central, lo que provoca un desgaste desigual y un contacto deficiente.
- La pieza se fija con dobles ápices y la pinza de corazón de pollo transmite fuerza, imposibilitando el mecanizado tanto del cono interno como del cono externo general.
4. Conclusión
Los dos métodos de mecanizar un cono descritos anteriormente utilizan relaciones de funciones trigonométricas para calcular los datos y luego ajustan el medio ángulo del cono indirectamente a través del indicador de cuadrante, lo que da como resultado el mecanizado del cono exterior y una mayor precisión del medio ángulo de el cono de la pieza de trabajo.
Estos métodos tienen importancia práctica en el mecanizado de conos externos utilizando máquinas herramienta estándar.