Basado en la teoría de optimización de la simulación de pruebas ortogonales, utilizando el ejemplo de una pieza de manguito de precisión de pared delgada específica y con el diseño de calidad de mecanizado como objetivo de optimización, los factores más importantes que influyen en el corte de la parte del manguito se examinan en una mejor combinación de soluciones para obtener los parámetros de proceso ideales para tornear la superficie exterior.
0. Introducción
“Made in China 2025” ha llevado a la industria manufacturera a mejorar los requisitos de calidad del procesamiento de productos. Las piezas de paredes delgadas se utilizan ampliamente debido a su peso ligero, bajo coste de consumo y otras ventajas notables. Sin embargo, como la tecnología y la experiencia aún no están maduras, estos productos a menudo sufren deformaciones en el procesamiento de piezas en el proceso de producción y procesamiento debido a parámetros de corte inadecuados, sujeción y selección de herramientas incorrectas, etc., lo que afecta la calidad del producto. Por lo tanto, el procesamiento eficiente de piezas de paredes delgadas se ha convertido en una necesidad urgente para que los ingenieros mecánicos resuelvan problemas de ingeniería y fabricación, lo que atrae a innumerables investigadores y científicos para realizar investigaciones e investigaciones en profundidad.
El equipo extranjero de M. Hareendran no solo estudió los parámetros óptimos del proceso para tornear piezas de paredes delgadas utilizando el software MATLAB, sino que también utilizó el software ANSYS para estudiar en profundidad la deformación de la pieza y el proceso de torneado. Finalmente, a través de la simulación virtual de errores de mecanizado y corte real, proporcionó una referencia de datos empíricos confiable, que es esencialmente consistente con la experiencia práctica de mecanizar piezas de paredes delgadas. S. Sanjeev. Sanjeev et al. utilizó un modelo empírico para mecanizar acero para herramientas H11 y utilizó el método de superficie de respuesta para identificar piezas de baja rigidez mediante un estudio en profundidad de los parámetros de corte (velocidad de corte, avance, profundidad de corte) y parámetros de la herramienta. La precisión y confiabilidad del modelo se verificaron mediante experimentos. Equipo nacional de Wang Xiangjun, etc. utilizó el software ANSYS para analizar los parámetros de proceso óptimos para el proceso de mecanizado de anillos de rodamientos de paredes delgadas mediante simulación. Los resultados del análisis cumplieron con los requisitos de tolerancia de forma y posición del aro del rodamiento y pudieron optimizar el trabajo con éxito. Xu Guangbin estudió el torneado de paredes delgadas y mejoró la optimización del programa propuesto desde la perspectiva de los parámetros de geometría de la herramienta y la sujeción de piezas de trabajo en varias piezas comunes de paredes delgadas para establecer una base sólida para el mecanizado de piezas de paredes delgadas. Deng Zhaoshuai también utilizó Deform-3D, una simulación de elementos finitos de diferentes velocidades al cortar acero 45#, y estudió el efecto de la velocidad de corte en la ley de desgaste de la herramienta y la relación entre la temperatura de corte y el desgaste de la herramienta para estudiar el mecanismo de desgaste de la herramienta. , para acelerar el proceso de corte y mejorar la optimización del proceso. Para estudiar el mecanismo de desgaste de la herramienta, una elección adecuada de la velocidad de corte proporciona una base de referencia. Además, Yue Caixu explicó la teoría básica de la tecnología de simulación de elementos finitos de corte de metales, los métodos técnicos y las áreas de aplicación práctica para brindarnos una mejor orientación.
Actualmente, la investigación paramétrica para tornear piezas de paredes delgadas aún no está completamente desarrollada. La programación de torneado CNC se basa principalmente en fórmulas teóricas y datos empíricos para determinar los parámetros de procesamiento, lo que causa muchos problemas en la producción de piezas de paredes delgadas. Sin embargo, con el continuo desarrollo de la tecnología de análisis de elementos finitos, la tecnología de ingeniería asistida por computadora (CAE) ha hecho posible explorar en profundidad el mecanismo intrínseco de la deformación rotacional, y los resultados de la investigación brindan un fuerte apoyo para una producción de mecanizado ordenada y eficiente. . La digitalización del proceso de edición y predicción de imágenes no solo se puede realizar, sino que también puede ahorrar una gran cantidad de recursos humanos, materiales y financieros, lo que defienden la mayoría de los científicos e ingenieros de ingeniería mecánica y crea gradualmente una ola de entusiasmo por la investigación.
En resumen, para determinar los parámetros de corte óptimos de una manga de pared delgada, este artículo se basa en el módulo de análisis de elementos finitos Naxtran integrado en el software NX1899 para analizar el campo de la estructura mecánica del proceso de torneado de la superficie del cilindro de la manga y el efectos de varias combinaciones ortogonales de parámetros de mecanizado para examinar la deformación de la pieza. Finalmente, se determinan las combinaciones óptimas de parámetros para el torneado CNC para mejorar la eficiencia y precisión del mecanizado de piezas de paredes delgadas. Luego, se determina la combinación óptima de parámetros para el torneado CNC para mejorar la eficiencia del mecanizado y la precisión de piezas de paredes delgadas.
1. Simulación de prueba ortogonal
1.1 Modelado geométrico
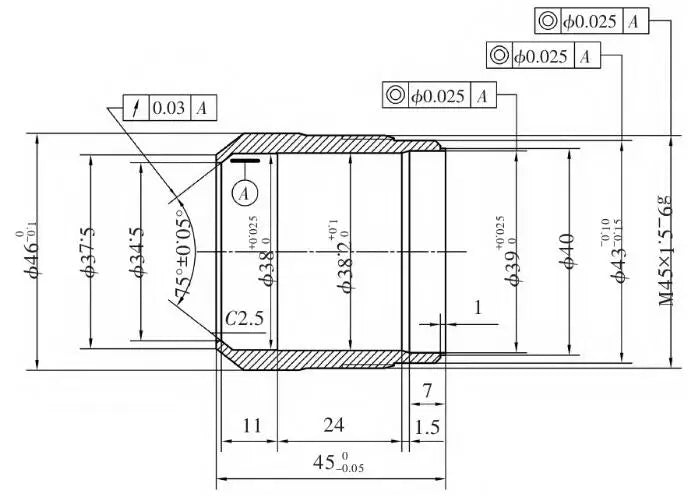
La Figura 1 muestra las partes objeto de este documento. El espesor mínimo de la pared radial es de sólo 2 mm en un lado. En todos los procesos de mecanizado, el torneado de la superficie exterior de la pieza tiene el mayor impacto en la rigidez de la pieza, pero también es un proceso fundamental para asegurar la precisión del mecanizado. Por ello, a la hora de optimizar los parámetros de ajuste se da prioridad al estudio de estas condiciones de trabajo. En este artículo se realiza el estudio del programa de sujeción para piezas de casquillos de paredes delgadas para determinar el uso del posicionamiento axial. Como se muestra en la Figura 2, las descripciones del programa de pieza específico y los pasos de instalación no se repiten. En estas condiciones, es necesario simplificar las operaciones de procesamiento con referencia a los requisitos de análisis estático del modelo relevante para facilitar la adquisición de resultados de datos confiables y al mismo tiempo evitar tediosos cálculos de simulación. Finalmente, después de completar el programa de sujeción axial después del procesamiento del modelo, se puede llamar al módulo de análisis de elementos finitos.
Figura 1 Dibujo de piezas de manguito de paredes delgadas.
1.2 Definición de propiedades materiales.
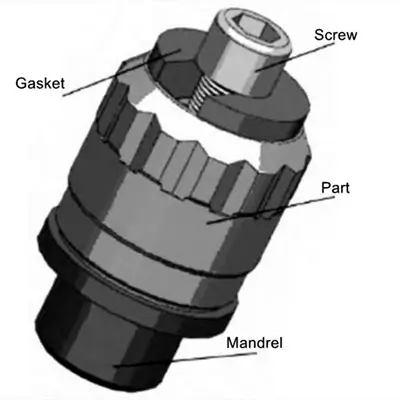
Figura 2: Número de programa de pieza Diagrama de modelo Accesorio axial
En el entorno FEM, la creación del modelo intrínseco del material se refiere a la curva de relación tensión-deformación del material correspondiente, que se utiliza para expresar el comportamiento de reacción del material bajo la acción de la carga. Es uno de los tres atributos principales del análisis estructural CAE. Para determinar efectivamente la deformación de la pieza en este modelo numérico, se realiza la siguiente simplificación: se supone que todas las piezas del modelo de material de la pieza son acero isotrópico 45# y el procesamiento real se debe a la fricción de alta temperatura. generado por el proceso de corte, provocado por la organización metalúrgica interna de los cambios de material y el proceso de transformación plástica, no se tiene en cuenta para completar la definición de todas las partes de las propiedades materiales del programa. Los principales parámetros mecánicos del material de acero 45# utilizado son una densidad de 7,83 g/cm 3 , un módulo de Young de 207 GPa, una relación de Poisson de 0,29 y un límite elástico de 355 MPa.
1.3 División de la red celular
La cuadrícula de celdas es portadora de datos computacionales para la simulación y el análisis CAE y es un paso importante en la configuración del preprocesamiento de la simulación. Para adaptar la partición de malla del modelo a diferentes partes y diversas estructuras complejas, este estudio utiliza una generación de malla rápida y altamente adaptable. Además, para la forma compleja de la pared, es más fácil codificar la malla tetraédrica. El tamaño de la celda de malla se divide en 2 mm y, al mismo tiempo, el proceso de cifrado de dos superficies asociado con el contacto de la pieza se cifra para mejorar la precisión de la transmisión de datos. Una vez completada la malla final, todo el modelo de malla de elementos finitos se muestra en la Figura 3.

Figura 3: Efecto de la delimitación de la malla
1.4 Configurar parámetros ortogonales
El diseño ortogonal de experimentos (también conocido como diseño DOE) es un método para diseñar pruebas multifactoriales y multinivel de manera científica, económica y eficiente como base teórica y se utiliza como un método de diseño eficiente. Tiene características científicas y razonables y una dispersión uniforme, lo que permite lograr los resultados de prueba deseados con menos pruebas, ciclos más cortos y costos más bajos. Por lo tanto, este método se utiliza cada vez más para identificar mejor los parámetros de este programa y mejorar la investigación.
Desde la perspectiva del proceso de mecanizado, existen muchos factores que afectan la precisión del torneado. Además de los tres elementos de corte, el ángulo de la herramienta, los materiales de corte, el líquido de corte, etc., el uso inadecuado puede causar defectos de precisión, astillamiento grave o incluso astillado de la herramienta y desperdicio de mecanizado. Por lo tanto, es obvio que la selección científica y razonable de los parámetros de corte es particularmente importante para el torneado, especialmente para el mecanizado de piezas con baja rigidez. Sin embargo, debido al tiempo y costo limitados de la investigación, solo los cuatro factores de velocidad del husillo, avance, retroceso y desviación de la herramienta principal se seleccionan como parámetros de optimización de este diseño experimental ortogonal. Estos parámetros se ajustan a tres valores de nivel razonables, y se utilizan fórmulas teóricas y datos empíricos para ajustar la velocidad a un nivel bajo de 800 rpm, el avance a 0,1 mm/rev, el movimiento inverso a 0, 3 mm, el movimiento principal desviación de la herramienta a 0,3 mm y la desviación de la herramienta principal a 0,3 mm. 0,3 mm, ángulo de deflexión de la herramienta principal de 45 °, realizado mediante cuatro factores y tres niveles de diseño del programa de prueba ortogonal L 9 (4 3 ), los factores de prueba ortogonales específicos y los valores de nivel correspondientes se muestran en la Tabla 1.
Tabla 1 Parámetros de prueba ortogonales
| Optimizar parámetros | Nivel bajo (1) | Nivel intermedio (2) | Alto nivel (3) |
| Velocidad del husillo (A) | 800 | 1200 | 1600 |
| Velocidad de alimentación (B) | 0.1 | 0,2 | 0.3 |
| Sobremordida (C) | 0.3 | 0,5 | 0,8 |
| Ángulo de desviación principal de la herramienta (D) | 45 | 75 | 90 |
Con respecto a la simulación de prueba ortogonal, diseño del esquema de combinación L 9 (4 3 ), consulte los datos en la Tabla 1 para la combinación de prueba ortogonal, en la que las letras mayúsculas corresponden a los cuatro factores de búsqueda diferentes, el número corresponde a la diferencia en el nivel de cada factor, el establecimiento de la combinación del Esquema L 9 (4 3 ) para los cuatro factores y tres niveles de un total de nueve combinaciones de la simulación de prueba para la fuente principal de cálculo del valor numérico del corte de fuerza. Por el contrario, la fuerza cortante se puede utilizar para el programa de fijación 2. La fuerza cortante se puede utilizar para aplicar la carga para el escenario de fijación 2, completando el diseño de los parámetros de prueba ortogonales entre los nueve escenarios de diseño.
1.5 Imposición de limitaciones de carga
Antes de aplicar cargas y restricciones en la configuración de la simulación, todas las piezas individuales deben estar conectadas de forma segura utilizando el comando Cara a Cara para crear el análisis de simulación completo. Como todo el programa de sujeción se basa en sujetar la superficie del extremo derecho del mandril con el mandril de tres mordazas conectado a la máquina herramienta, el uso de "restricciones personalizadas", además de liberar los grados de libertad de rotación alrededor del eje axial de la Chuck, todo se arreglará. La carga se aplica primero; toda la pieza está sujeta a la gravedad del campo gravitacional bajo la acción de G. La dirección sigue la dirección radial de las piezas giratorias; en segundo lugar, la fuerza centrífuga de rotación del dispositivo proviene del eje del eje central de la parte giratoria, por lo que el centro del eje central sirve como el centro de la superficie del extremo derecho de la parte giratoria, y el valor correspondiente de la Se suma la carga de rotación F. 1 ; Finalmente, las piezas del manguito de paredes delgadas también están expuestas a la fuerza de corte principal F debido a la presión radial de la herramienta. 2 Los valores específicos se pueden asignar a los datos correspondientes en la tabla de combinaciones de pruebas ortogonales anterior. Esto completa las limitaciones de simulación y aplicación de carga de un programa específico de posicionamiento y sujeción axial. Una vez completada la configuración, puede comenzar el proceso de solución hidrostática.
Con referencia al método descrito anteriormente de aplicar restricciones de carga para completar la configuración de simulación del programa de prueba ortogonal restante, el proceso específico no se repite. Finalmente, los resultados del posprocesamiento correspondientes a los nueve escenarios diferentes se obtienen mediante configuraciones de simulación repetidas y un largo tiempo de espera. Al mismo tiempo, después de completar el resumen de los datos de desplazamiento obtenidos mediante el cálculo y el procesamiento correspondiente, se obtienen nueve factores diferentes por debajo del nivel del valor promedio del desplazamiento de deformación de la pieza de trabajo y tres tipos de valores de diferencia extremos, específicamente como se muestra en Tabla 2.
Tabla 2: Prueba ortogonal de valores de programas individuales
| factor | Velocidad del husillo/(rpm -1 ) | Velocidad de alimentación/(mm.r -1 ) | Profundidad de corte/mm | Ángulo de desviación principal de la herramienta/(°) | Fuerza de corte principal/N | Desplazamiento/μm | Tensión/MPa |
| examen 1 | 800 | 0.1 | 0.3 | 45 | 109,9 | 1.13 | 18,77 |
| Intento 2 | 800 | 0,2 | 0,5 | 75 | 284,9 | 2.91 | 48,65 |
| examen 3 | 800 | 0.3 | 0,8 | 90 | 612,5 | 6.25 | 104,6 |
| examen 4 | 1200 | 0,2 | 0.3 | 90 | 169,5 | 1,73 | 28,94 |
| examen 5 | 1200 | 0.3 | 0,5 | 45 | 417,5 | 4.26 | 71.3 |
| examen 6 | 1200 | 0.1 | 0,8 | 75 | 271.1 | 2.77 | 46,29 |
| examen 7 | 1600 | 0.3 | 0.3 | 75 | 231,7 | 2.35 | 39,46 |
| examen 8 | 1600 | 0.1 | 0,5 | 90 | 167,9 | 1.71 | 28,66 |
| Intento 9 | 1600 | 0,2 | 0,8 | 45 | 492,8 | 5.02 | 84,15 |
| Promedio (cambio) | 3.43 | 1,87 | 1.74 | 3.47 | – | – | – |
| 2.92 | 3.22 | 2,96 | 2,68 | – | – | – | |
| 3.03 | 4.29 | 4.68 | 3.23 | – | – | – | |
| Rango | 0,51 | 2.42 | 2.94 | 0,79 | – | – | – |
| Superioridad teórica | un 2 | segundo 1 | C 1 | D2 | – | – | – |
2. Cálculo y análisis de simulación.
Después de analizar los factores correspondientes, el valor promedio y la desviación extrema en la Tabla 2, se encuentra que al reducir el desplazamiento de deformación de piezas de paredes delgadas, el torneado es el parámetro objetivo de optimización. El factor de diseño del avance inverso tiene la mayor influencia, seguido del avance, luego el ángulo de desviación principal de la herramienta y finalmente la velocidad del husillo. Entre ellos, el grado de influencia del ángulo de desviación principal de la herramienta y la velocidad de rotación sobre la pieza de trabajo es similar. Por el contrario, el grado de influencia del avance inverso y el avance inverso es mucho mayor que los otros dos factores, por lo que se puede concluir tentativamente que el diseño apropiado de avance y avance inverso es el parámetro clave del proceso que decide garantizar la precisión de la rotación de estos. piezas de casquillo de paredes delgadas.
Además, al comparar el promedio grupal de desplazamiento de cada factor para obtener el mejor nivel de cada factor y el promedio de los 9 grupos de factores diferentes, se puede concluir aproximadamente que la combinación teórica óptima bajo la prueba de simulación ortogonal para A 2 b 1 C 1 D 2 que es diferente de los 9 grupos de datos en la combinación de prueba 1 del programa (A 1 b 1 C 1 D 1 ), y para filtrar lo mejor de la combinación teóricamente mejor y ortogonalmente mejor de dos programas, el La prueba teóricamente mejor y la prueba ortogonal se realizaron bajo las mismas condiciones de análisis de simulación estática. Los resultados finales del cálculo numérico se muestran en la Figura 4 y la Figura 5.

Figura 4 Mapa general de desplazamiento del dispositivo
Los resultados del cálculo numérico muestran que bajo las condiciones de una fuerza de corte principal de 101,6 N, el mejor programa teóricamente tiene un desplazamiento de deformación de la pieza de 1,04 μm, lo que significa una reducción en el desplazamiento de deformación de aproximadamente el 8% en comparación con el programa de prueba 1. El valor de tensión de Von Mises es de sólo 17,35 MPa. Se puede concluir que los valores calculados por el programa son mejores que las pruebas ortogonales enumeradas en los nueve grupos de opciones de diseño y, por lo tanto, representan la solución ideal para el manguito de paredes delgadas. Por lo tanto, la combinación óptima de parámetros de giro para la superficie cilíndrica de la pieza de trabajo para este casquillo de pared delgada es la siguiente: al seleccionar un ángulo de desplazamiento de la herramienta principal de 75°, la velocidad del husillo es de 1200 rpm, el avance se establece en 0,1 mm /rev y volver a 0,3 mm.

Fig. 5 Nubes de tensión integrales de Von Mises
3. Conclusión
Basado en la teoría de pruebas y el análisis ortogonal, este artículo busca la combinación óptima de parámetros de proceso de velocidad del husillo, avance, retorno y ángulo de deflexión de la herramienta principal para el proceso de mecanizado de torneado cilíndrico de piezas de bujes de paredes delgadas. Se basa en el software de análisis de elementos finitos NX para realizar cálculos de campo estático estructural y análisis de programas de prueba ortogonales de forma secuencial para obtener los valores de desplazamiento y deformación de las piezas y sus distribuciones bajo diferentes parámetros de proceso. Las conclusiones relevantes son las siguientes:
- 1) Para piezas de casquillo de paredes delgadas, la deformación durante el torneado cilíndrico aumenta significativamente al aumentar el movimiento hacia atrás y el avance. Por lo tanto, para garantizar la precisión y la calidad de las piezas de paredes delgadas, estos dos factores clave deben seleccionarse de manera científica y efectiva. Sin embargo, la influencia de la velocidad del husillo y el ángulo de desviación principal de la herramienta sobre la deformación de las piezas es menor. Aún es necesario elegir sabiamente el papel secundario.
- 2) El uso de pruebas ortogonales combinadas con elementos finitos para piezas de paredes delgadas o la combinación de pruebas ortogonales y elementos finitos proporciona pautas teóricas importantes para formular parámetros de proceso para piezas de paredes delgadas y al mismo tiempo proporciona una sólida garantía para mejorar la precisión del mecanizado de las piezas. y reducir la deformación por mecanizado de piezas de baja rigidez. Además, abre una nueva forma de pensar y un nuevo método para explorar la tecnología de la ingeniería.