Caso uno
Regalado:
- Masa del disco M=50 kg
- Diámetro del disco D=500 mm
- Velocidad máxima del disco 60 rpm
Seleccione el servomotor y el engranaje reductor, el diagrama de componentes es el siguiente:
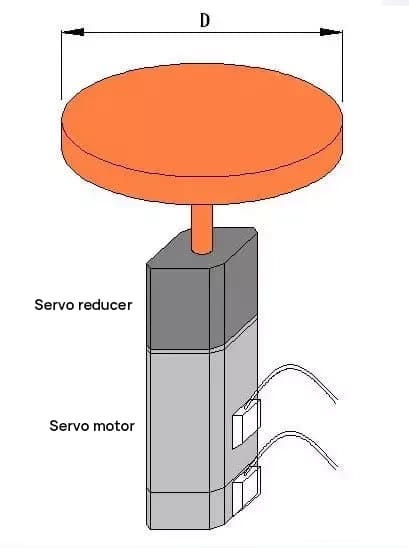
Cálculo del momento de inercia para la rotación del disco.
J. l = MD 2 /8 = 50 * 50 2 / 8 = 15625 (kg cm 2 )
Suponiendo una relación de reducción de engranajes de 1:R, la inercia de carga reflejada en el eje del servomotor es 15625/R 2 .
Según el principio de que la inercia de la carga debe ser menor que tres veces la inercia del rotor J M del motor,
si se selecciona un motor de 400 W, J M = 0,277 (kg cm 2 ),
entonces: 15625/ R2 < 3*0,277, R2 > 18803, R > 137,
la velocidad de salida = 3000/137 = 22 (rpm),
que no cumple con el requisito.
Si se selecciona un motor de 500 W, J M = 8,17 (kg cm 2 ),
entonces: 15625/ R2 < 3*8,17, R2 > 637, R > 25,
la velocidad de salida = 2000/25 = 80 (rpm),
que satisface el requisito.
Este tipo de transmisión tiene una resistencia mínima, por lo que se ignoran los cálculos de par.
Caso dos
Regalado:
- Peso de carga M = 50 kg
- Diámetro de la rueda de la correa síncrona D = 120 mm
- Relación de reducción R 1 = 10, R 2 = 2
- Coeficiente de fricción entre carga y mesa de la máquina µ = 0,6
- Velocidad máxima de movimiento de la carga: 30 m/min
- Tiempo para que la carga acelere desde el reposo hasta la velocidad máxima: 200ms
Ignorando el peso de cada rueda en la cinta transportadora,
¿Cuál es el requisito mínimo de potencia para que un motor impulse tal carga?
El diagrama esquemático del componente es el siguiente:
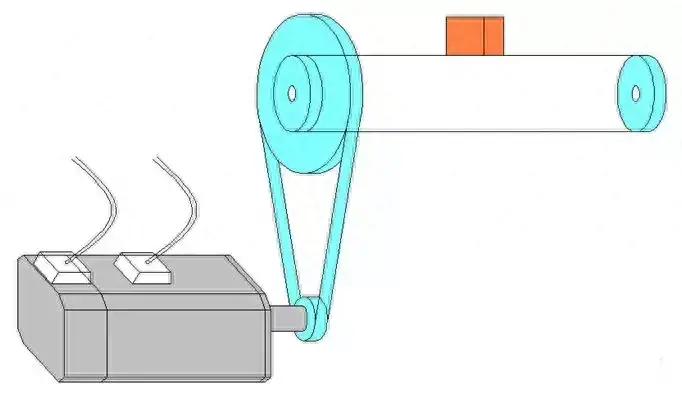
1. Cálculo de la inercia de la carga reflejada sobre el eje del motor:
JL = M * D 2 /4/R 1 2
= 50 * 144/4/100
= 18 (kg cm 2 )
Según el principio de que la inercia de la carga debe ser inferior a tres veces la inercia del rotor del motor (JM):
J. M > 6 (kg cm 2 )
2. Cálculo del par necesario para impulsar la carga del motor:
Torque necesario para superar la fricción:
Tf =M*g*µ*(D/2)/R 2 /R 1
= 50 * 9,8 * 0,6 * 0,06/2/10
= 0,882 (N·m)
Torque requerido para la aceleración:
Ta = M * a * (D / 2) / R 2 /R 1
= 50 * (30/60/0,2) * 0,06/2/10
= 0,375 (N·m)
El par nominal del servomotor debe ser mayor que T f y el par máximo debe ser mayor que T f +T a .
3. Cálculo de la velocidad requerida del motor:
norte = v / (πD) * R 1
= 30 / (3,14 * 0,12) * 10
= 796 (rpm)
Caso tres
Regalado:
- Peso de carga M = 200 kg
- Paso de tornillo PB = 20 mm
- Diámetro del tornillo DB = 50 mm
- Peso del tornillo MB = 40 kg
- Coeficiente de fricción µ = 0,2
- Eficiencia mecánica η = 0,9
- Velocidad de movimiento de la carga V = 30 m/min
- Tiempo total de movimiento t = 1,4 s
- Tiempo de aceleración y desaceleración t 1 = t 3 = 0,2 s
- Tiempo de descanso t 4 = 0,3 s
Seleccione el servomotor con la potencia mínima que cumpla con los requisitos de carga,
El diagrama de componentes es el siguiente:
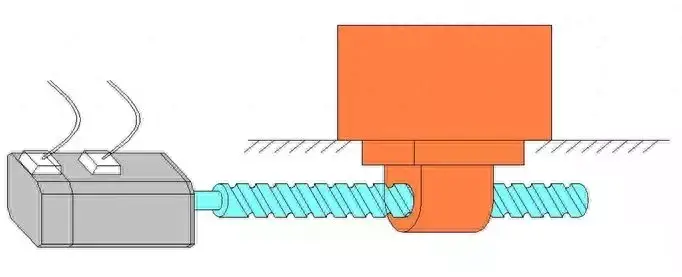
1. Cálculo de la inercia de carga convertida al eje del motor
Inercia de carga del peso convertido al eje del motor.
J.C =M*(PB/2π)²
= 200 * (2/6,28)²
= 20,29 (kg·cm²)
La inercia rotacional del tornillo.
J.B =M B *D B² /8
= 40*25/8
= 125 (kg·cm²)
Inercia de carga total
JL = JW + JB = 145,29 (kg cm²)
2. Cálculo de la velocidad del motor.
Velocidad requerida del motor
N=V/PB
= 30/0,02
= 1500 (rpm)
3. Cálculo del par requerido para impulsar la carga del motor.
El par necesario para superar la fricción.
T f =M*g*µ*PB/2π/η
= 200*9,8*0,2*0,02/2π/0,9
= 1,387 (N·m)
Torque requerido cuando el peso se acelera
T A1 =M*a*PB/2π/η
= 200 * (30/60 / 0,2) * 0,02 / 2π / 0,9
= 1,769 (N·m)
Torque requerido cuando el tornillo está acelerando
T A2 = JB * α / η
=J B *(N*2π/60/t 1 ) /η
= 0,0125 * (1500 * 6,28/60/0,2)/0,9
= 10,903 (N·m)
Par total requerido para la aceleración
T A =T A1 +T A2 = 12,672 (N·m)
4. Selección del servomotor
Par nominal del servomotor
T > T f y T > Trms
Par máximo del servomotor
T máx. >T f +T A
Finalmente se seleccionó el motor ECMA-E31820ES.

























































