1. Teoría de la tensión máxima de tracción (la primera teoría de la resistencia es la tensión principal máxima):
Esta teoría se conoce comúnmente como la primera teoría de la fuerza. Afirma que la principal causa de falla es la tensión máxima de tracción. Si la primera tensión principal alcanza el límite de resistencia a la tracción uniaxial, independientemente de la complejidad o simplicidad del estado de tensión, provocará una fractura.
Forma de falla: fractura
Condiciones de daño: σ1 =σb
Condición de resistencia: σ1≤(σ)
Los experimentos han demostrado que esta teoría de la resistencia puede explicar mejor el fenómeno de fractura de materiales frágiles como la piedra y el hierro fundido, particularmente en áreas donde se localiza la tensión máxima de tracción. Sin embargo, no es adecuado para casos sin tensión de tracción, como compresión unidireccional o compresión triple.
Desventaja: No considera los otros dos voltajes principales.
Ámbito de aplicación: esta teoría es adecuada para la tensión de materiales frágiles, como el estiramiento y la torsión del hierro fundido.
2. Teoría de la deformación lineal de alargamiento máximo (la segunda teoría de la resistencia es la deformación principal máxima)
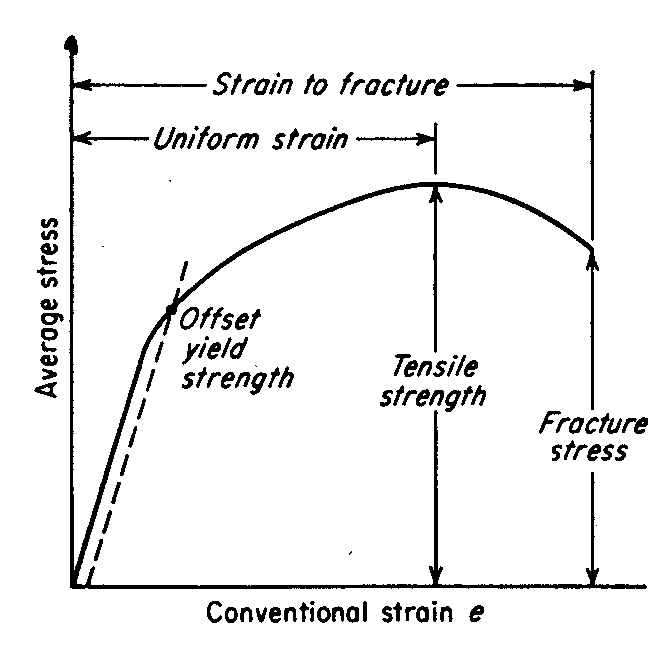
Esta teoría se conoce comúnmente como la segunda teoría de la fuerza. Postula que la principal causa de falla es la deformación por estiramiento lineal máximo. Si la primera deformación principal alcanza el valor límite de la tensión uniaxial, independientemente de la complejidad o simplicidad del estado de tensión, se produce una fractura.
Supuesto de falla: la deformación por alargamiento máximo alcanza el límite de tensión simple (suponiendo que la ley de Hooke aún se pueda usar para calcular hasta que se produzca la fractura).
Forma de falla: fractura
Condiciones de fractura frágil: ε1 = εu = σb/E;
ε1 = 1/E (σ1−μ(σ2+σ3));
Condiciones de daño: σ1−μ(σ2+σ3) = σb;
Condición de resistencia: σ1−μ(σ2+σ3)≤(σ)
Los experimentos han demostrado que esta teoría de la resistencia puede explicar mejor el fenómeno de fractura de materiales frágiles como la piedra y el hormigón bajo tensión axial. Sin embargo, rara vez se ha utilizado porque sus resultados experimentales son consistentes sólo con unos pocos materiales y no pueden explicar en gran medida la ley general de falla por fractura frágil.
Desventaja: No explica la ley general de falla por fractura frágil.
Ámbito de aplicación: Esta teoría es adecuada para la compresión axial de piedra y hormigón.
3. Teoría del esfuerzo cortante máximo (la tercera teoría de la resistencia, a saber, la resistencia de Tresca):
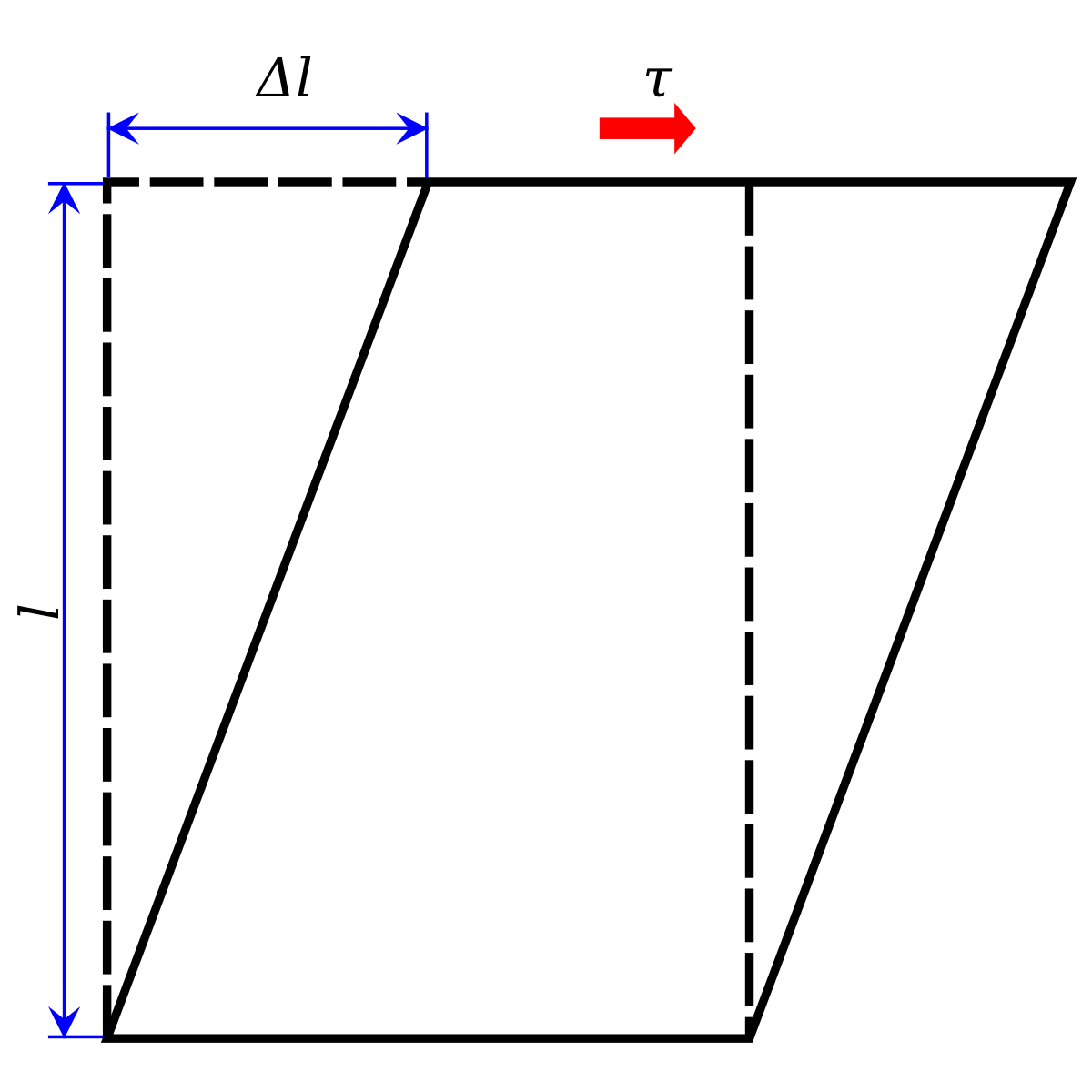
Esta teoría, conocida como tercera teoría de la resistencia, postula que la principal causa de falla es el esfuerzo cortante máximo (τmax). La teoría establece que, independientemente de la complejidad o simplicidad del estado de tensión, una vez que la tensión cortante máxima alcanza el valor final de la tensión cortante bajo tensión uniaxial, se producirá fluencia.
El supuesto de falla es que cuando el esfuerzo cortante máximo en un estado de esfuerzo complejo alcanza el límite del esfuerzo cortante del material durante la tensión y compresión simples, la falla ocurrirá en forma de fluencia. El principal factor que contribuye a la falla es el esfuerzo cortante máximo, que es igual al esfuerzo cortante último (τmax=τu=σs/2).
La condición de fallo de rendimiento se define como τmax=1/2(σ1−σ3), y las condiciones de daño se cumplen cuando σ1−σ3=σs. La condición de resistencia se expresa como σ1−σ3≤(σ).
Los experimentos han demostrado que esta teoría explica mejor la deformación plástica de los materiales plásticos. Sin embargo, cabe señalar que esta teoría no tiene en cuenta la influencia de 2σ y, como resultado, los componentes diseñados con base en esta teoría tienden a ser demasiado conservadores.
Desventajas: ninguna influencia 2 σ
Ámbito de aplicación: adecuado para condiciones generales de materiales plásticos.
La forma es simple, el concepto es claro y la maquinaria se utiliza ampliamente.
Pero el resultado teórico es más seguro que el real.
4. Teoría energética específica del cambio de forma (cuarta teoría de la fuerza, a saber, la fuerza de von Mises)
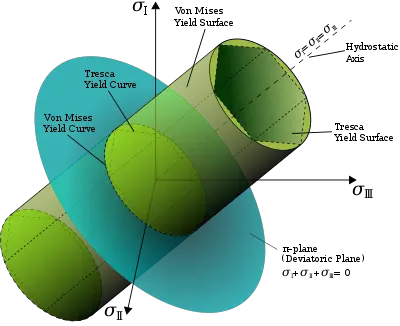
Esta teoría se conoce como la cuarta teoría de la resistencia y postula que la razón por la que un material cede es la energía específica (DU) del cambio de forma que alcanza un cierto valor umbral, independientemente del estado de tensión.
Las condiciones de daño se definen como 1/2(σ1−σ2)2+2(σ2−σ3)2+(σ3−σ1)2=σs, y la condición de resistencia se da como σr4= 1/2(σ1− σ2) 2+ (σ2−σ3)2 + (σ3−σ1)2≤(σ).
Los datos experimentales de pruebas de tubos delgados sobre diversos materiales (acero, cobre, aluminio) mostraron que la teoría de la energía específica del cambio de forma está más en línea con los resultados experimentales en comparación con la tercera teoría de la resistencia.
Se puede establecer una forma unificada de las cuatro teorías de resistencia teniendo una tensión equivalente (σrn) que tenga una expresión unificada de la condición de resistencia (σrn≤(σ)). El voltaje equivalente se puede expresar de la siguiente manera:
σr1=σ 1≤(σ)
σr2=σ1−μ(σ2+σ3)≤(σ)
σr3=σ1−σ3≤ (σ)
σr4= 1/2(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2≤ (σ)
5. Teoría de la fuerza de Mohr
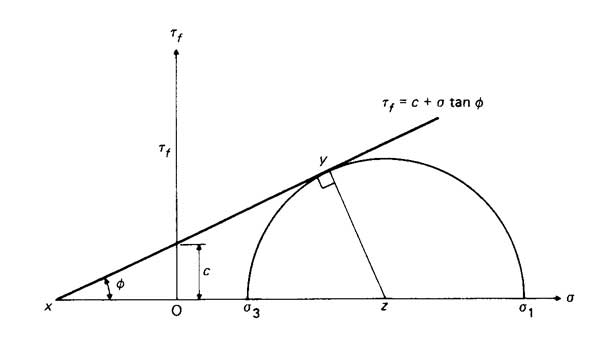
La teoría de la resistencia de Mohr no se basa en el supuesto de que la falla en los materiales sea causada por un solo factor (como tensión, deformación o energía específica) que alcanza su valor límite. Más bien, es una teoría de la resistencia basada en los resultados de pruebas de falla de materiales bajo diversos estados de tensión.
Esta teoría considera las diferencias entre las resistencias a la tracción y a la compresión de los materiales, reconoce el esfuerzo cortante máximo como la principal causa de fluencia y tiene en cuenta la influencia del esfuerzo normal en el plano de corte.
Aunque la teoría de la resistencia de Mohr reconoce las diferentes capacidades de tracción y compresión de los materiales, lo cual es consistente con materiales frágiles (como roca y concreto), no toma en cuenta la influencia de la tensión principal intermedia 2a, lo cual es una limitación de la teoría.
6. Ámbito de aplicación de la teoría de la resistencia.
La resistencia de un material no sólo está determinada por la naturaleza del material, sino también por el estado de tensión en el punto de falla.
Los materiales frágiles generalmente se analizan utilizando la teoría de la resistencia a la fractura frágil o la teoría de la resistencia de Mohr, mientras que los materiales plásticos se analizan utilizando la teoría del límite elástico.
Sin embargo, el modo de falla en los materiales también está relacionado con el estado de tensión. Por ejemplo, bajo la condición de tensión de tracción tridimensional, ya sea un material plástico o frágil, fallará en forma de fractura y se debe utilizar la teoría de la tensión de tracción máxima. En el caso de tensión de compresión tridimensional, se produce deformación plástica y se debe utilizar la tercera o cuarta teoría de la resistencia.