Doblado en L
1) Factores que determinan la flexión L mínima
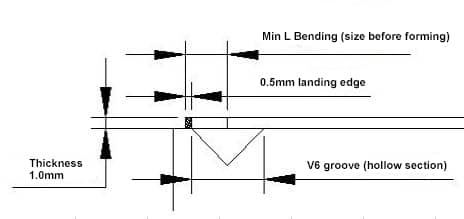
Debido a que el centro de la ranura en V de la plegadora es hueco, durante la formación, la curva del borde debe ser más grande que la sección hueca, y el tamaño específico del borde del asiento varía en la producción de diferentes empresas (la sección inferior de la plegadora Si se utiliza la ranura en V durante mucho tiempo, el ángulo R aumenta, lo que hace que la distancia del borde de desecho aumente en consecuencia; de lo contrario, se producirá un "deslizamiento").
2) Fórmula de reducción (empírica): 6 T/2+0,5+(1,8 T/2)
3) Como muestra la imagen a continuación, cuando T = 1, K = 1,8 * 1, la flexión L mínima es 3 + 0,5 + 0,9 = 4,4
| Ranura en V/grosor | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | dieciséis | 18 |
| 0,5 | 2.5 | 3 | ||||||||||
| 0,8 | 3.2 | 3.7 | 4.2 | |||||||||
| 1 | 3.5 | 4 | 4.5 | 5 | 5.5 | |||||||
| 1.2 | 3.5 | 4 | 4.5 | 5 | 5.5 | |||||||
| 1.5 | 4.8 | 5.2 | 5.8 | 6.2 | 6.8 | |||||||
| dos | 7.5 | 8.5 | ||||||||||
| 3 | 11 | 12 | ||||||||||
| 4 | 15 | dieciséis | ||||||||||
| 5 | ||||||||||||
| 19 | 20 | |||||||||||
| 22 | 24 | 26 | 28 | 30 |
plegado en U
1) Tipos de curvatura en U
A. Conformación regular doblando punzón
B. Dobladillo inverso con junta (primero plegado a 30°, colocando una junta adecuada en el medio y luego dobladillo)
2) Factores que determinan la flexión mínima en forma de U
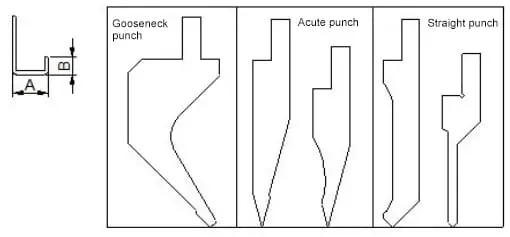
- Perfora formas (como se muestra en la siguiente imagen).
A juzgar por el molde de punzonado común, el mejor para doblar en U es el “punzón de cuello de cisne”, que tiene varios tipos y está sujeto específicamente a los requisitos de varias empresas.
- Tamaño de plegado (como se muestra en la siguiente imagen).
La creciente relación entre dos tamaños:
Cuanto más larga es A, más larga es B.
3 ) Fórmula de reducción (valor empírico del punzón de cuello de cisne)
◆ Hoja de 0,5 mm:
Flexión en U mínima: A = 7,67, B = 0,5, flexión en L mínima = 3,0
Valor creciente: cada vez que A aumenta en 1 mm, B aumenta en 1,87 en consecuencia.
Fórmula: Cuando se conoce el tamaño A, entonces el tamaño B = (A-7.67)/T* valor creciente + el valor mínimo de flexión L de esta placa
Por ejemplo,
cuando A=15, entonces B=(15-7,67)/0,5*1,87+3,0=30,4
Cuando se conoce el tamaño B, entonces el tamaño A = (B- el valor mínimo de flexión L de esta placa)/valor creciente *T+7.67
Por ejemplo,
cuando B=30.4, entonces A=(30.4-3)/1.87*0.5+7.67=15
◆ hoja de 0,8 mm
Tamaño mínimo de plegado en U A = 8,5, tamaño B = 0,8, mínimo de plegado en L = 4,2。
Valor creciente: 1,87/0,5*0,8=2,99
◆ Hoja de 1,0 MM
Tamaño mínimo de plegado en U A = 8,94, tamaño B = 1,0, mínimo de plegado en L = 4,5
Valor creciente: 1,87/0,5*1,0=3,7
◆ Hoja de 1,2 mm.
Tamaño mínimo de plegado en U A = 9,3, B = 1,2, mínimo de plegado en L = 4,5
Valor creciente: 1,87/0,5*1,2=4,5
◆ Hoja de 1,5 mm.
Tamaño mínimo de plegado en U A = 10,3, B = 1,5, mínimo de plegado en L = 6,2
Valor creciente: 1,87/0,5*1,5=5,5
◆ Hoja de 2,0 mm.
Tamaño mínimo de plegado en U A = 12,7, B = 2,0, mínimo de plegado en L = 12,0
Valor creciente: 1,87/0,5*2=7,4
Los grados:
- Cuando el tamaño A excede los 85,0 mm y el tamaño B excede los 60,0 mm, esta fórmula no es aplicable.
- Tabla adjunta: A= valor de prueba, B= flexión mínima L, K= valor de prueba
| Espesor | Talla única (mín.) | Tamaño B (mín.) | k |
|---|---|---|---|
| 0,5 | 7,67 | 3 | 1,87 |
| 0,8 | 8.5 | 4.2 | 2,99 |
| 1 | 8.94 | 4.5 | 3.7 |
| 1.2 | 9.3 | 4.5 | 4.5 |
| 1.5 | 10.3 | 6.2 | 5.5 |
| dos | 12.7 | 12 | 7.4 |
Relacionado: Calculadora de resistencia a la flexión en forma de V y U
Plegado en Z
1) Tipos de plegado en Z
- Cuando H es mayor o igual a 5T, calculando según dos curvas de 90°.
- Cuando H es menor que 5T, la formación única es suficiente
2) Los principales factores que afectan el valor mínimo de flexión en Z son el ancho de la ranura en V y la distancia desde el centro de la ranura en V hasta el borde.
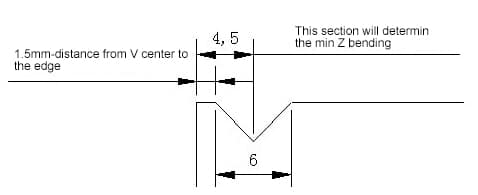
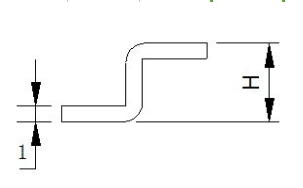
3) Fórmula: 6 T/2+distancia desde el borde de la ranura V+(1,8 T/2)+T(ver imagen)
Por ejemplo, en el caso de una placa de 1,0 mm, hasta una distancia al borde = 1,5, entonces el mínimo de flexión en Z H = 6 1/2+1,5+(1,8 1/2)+1= 6,4.
Cálculo del borde mínimo de flexión de un pliegue.
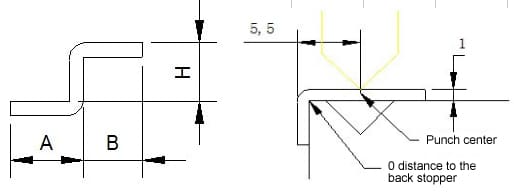
El estado inicial de la curva L se muestra en la siguiente ilustración:
Tabla de referencia para el doblado interno R y la altura mínima de doblado de láminas laminadas en frío
| No. | Espesor | Ancho de ranura | Matriz convexa R | Altura mínima de flexión |
| 1 | 0,5 | 4 | 0,2 | 3 |
| dos | 0,6 | 4 | 0,2 | 3.2 |
| 3 | 0,8 | 5 | 0,8/0,2 | 3.7 |
| 4 | 1.0 | 6 | 1/0.2 | 4.4 |
| 5 | 1.2 | 8/6 | 1/0.2 | 5,5/4,5 |
| 6 | 1.5 | 8/10 | 1/0.2 | 6,8/5,8 |
| 7 | 2.0 | 12 | 1,5/0,5 | 8.3 |
| 8 | 2.5 | 16/14 | 1,5/0,5 | 10,7/9,7 |
| 9 | 3.0 | 18 | 2/0,5 | 12.1 |
| 10 | 3.5 | 20 | dos | 13.5 |
| 11 | 4.0 | 25 | 3 | 16.5 |
El estado inicial de la curva Z se muestra en la siguiente ilustración:
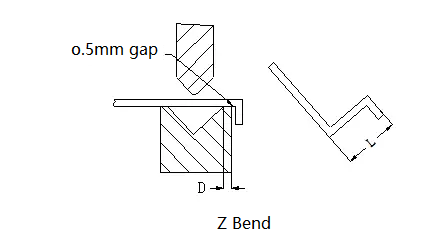
El tamaño mínimo de plegado (L) de chapa correspondiente al plegado en Z para materiales con diferentes espesores se muestra en la siguiente tabla:
| No. | Espesor | Ancho de ranura | Matriz convexa R | Altura de flexión Z |
| 1 | 0,5 | 4 | 0,2 | 8.5 |
| dos | 0,6 | 4 | 0,2 | 8.8 |
| 3 | 0,8 | 5 | 0,8/0,2 | 9.5 |
| 4 | 1.0 | 6 | 1/0.2 | 10.4 |
| 5 | 1.2 | 8/6 | 1/0.2 | 11,7/10,7 |
| 6 | 1.5 | 8/10 | 1/0.2 | 13,3/12,3 |
| 7 | 2.0 | 12 | 1,5/0,5 | 14.3 |
| 8 | 2.5 | 16/14 | 1,5/0,5 | 18,2/17,2 |
| 9 | 3.0 | 18 | 2/0,5 | 20.1 |
| 10 | 3.5 | 20 | dos | 22 |
| 11 | 4.0 | 25 | 3 | 25,5 |

























































