En el campo del diseño de chapa, a menudo se escuchan términos como margen de flexión, margen de flexión y factor K. Pero ¿qué significan exactamente estos términos? ¿Y cómo podemos calcularlos?
En esta publicación, proporcionaremos respuestas detalladas a estas preguntas.
1 . Introducción al método de cálculo de chapa metálica
Los ingenieros y vendedores involucrados en el diseño y producción de piezas de chapa utilizan varios algoritmos para calcular la longitud real del material en su estado desplegado para garantizar las dimensiones deseadas de la pieza después del doblado y el conformado final.
El método más utilizado es la sencilla “regla del pellizco del dedo”, un algoritmo basado en la experiencia personal, que tiene en cuenta factores como el tipo y espesor del material, el radio y ángulo de curvatura, el tipo de máquina y la velocidad. de flexión.
Con el surgimiento de la tecnología informática, el diseño asistido por computadora (CAD) se utiliza cada vez más para aprovechar las capacidades analíticas y computacionales superiores de la computadora.
Sin embargo, incluso cuando un programa de ordenador simula el plegado o el despliegue de una chapa metálica, sigue necesitando un método para realizar un cálculo preciso.
La mayoría de los sistemas comerciales de modelado de sólidos CAD y 3D brindan una solución general y poderosa para esto y generalmente son compatibles con el método de regla de pellizco original y ofrecen opciones de personalización para insertar contenido específico en su proceso de cálculo.
SolidWorks es líder en ofrecer esta capacidad para el diseño de chapa.
En conclusión, hoy en día se adoptan ampliamente dos algoritmos populares de doblado de chapa metálica: uno basado en la tolerancia de doblado y otro basado en la deducción de doblado.
Para mejorar la comprensión de los lectores de los conceptos básicos en el cálculo del diseño de chapa, se resumirán y explicarán los siguientes puntos:
- Las definiciones de los dos algoritmos de plegado: tolerancia de plegado y deducción de plegado, y su conexión con la geometría real de la chapa.
- La relación entre la deducción de pliegues y el margen de pliegues y cómo los usuarios que utilizan el algoritmo de deducción de pliegues pueden convertir fácilmente sus datos al algoritmo de margen de pliegues.
- La definición del factor K, su uso práctico y el rango de valores del factor K aplicables para diferentes tipos de materiales.
2. Método de tolerancia a la flexión
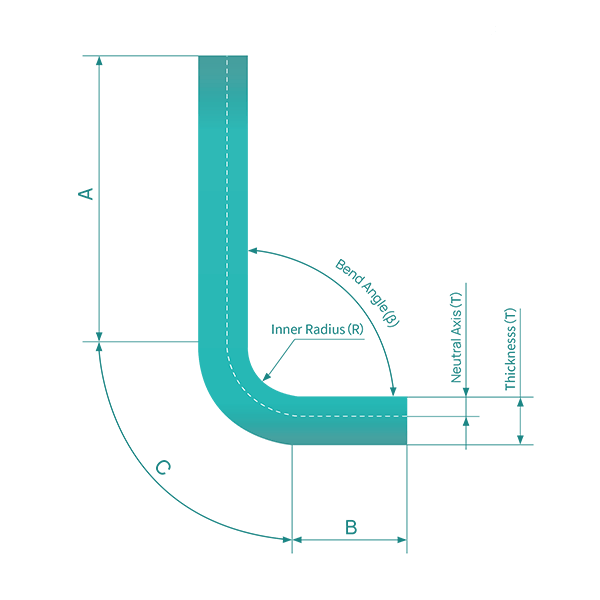
Para obtener una comprensión más clara de la tolerancia a la flexión, consulte la Figura 1, que ilustra una flexión única en un componente de chapa metálica. La figura 2 muestra la pieza en su estado desplegado.
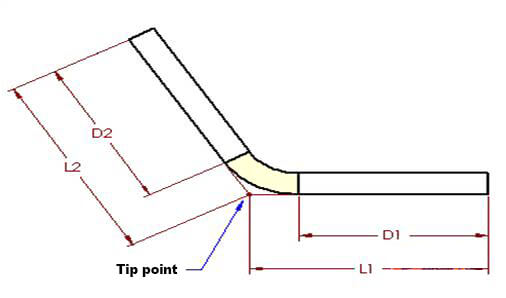
Figura 1
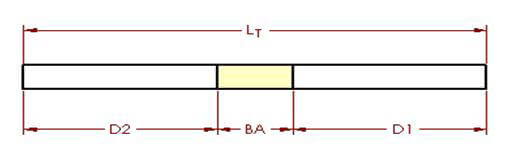
Figura 2
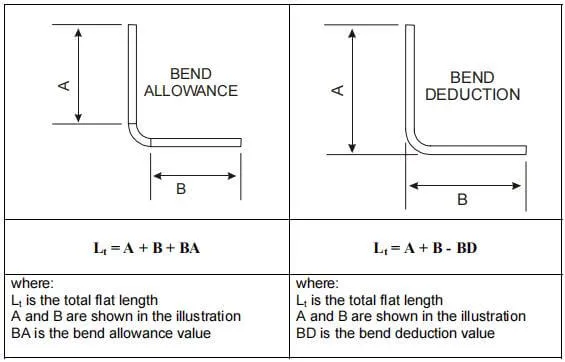
El algoritmo de margen de flexión describe la longitud desplegada (LT) de una pieza de chapa metálica como la suma de las longitudes de cada segmento después de aplanar la pieza, más la longitud del área de flexión aplanada.
La tolerancia de plegado (BA) representa la longitud del área de plegado aplanada. Así, la longitud total de la pieza se puede expresar como la ecuación (1):
LT = D1 + D2 + BA (1)
El área de flexión (ilustrada en amarillo claro en la ilustración) es el área que teóricamente sufre deformación durante el proceso de flexión.
Para determinar la geometría de la pieza desplegada, siga estos pasos:
- Corta el área doblada de la parte doblada.
- Coloque las dos secciones restantes sobre una superficie plana.
- Calcule la longitud del área de curvatura aplanada.
- Une el área de pliegue aplanada entre las dos secciones planas y el resultado será la pieza desplegada deseada.
La tarea de determinar la longitud del área de flexión aplanada, representada por BA en la figura, es un poco más desafiante.
El valor BA varía según factores como el tipo de material, el espesor del material, el radio y ángulo de curvatura, así como el proceso de curvatura, el tipo de máquina y la velocidad de la máquina.
El valor BA se puede obtener de varias fuentes, incluidos proveedores de materiales de chapa, datos experimentales, experiencia y manuales de ingeniería.
En SolidWorks, puede ingresar valores BA directamente o usar el factor K (que se discutirá más adelante) para calcular los valores.
El método de la mesa de plegado es la forma más precisa de especificar diferentes tolerancias de plegado para diferentes situaciones con diferentes espesores, radios y ángulos.
Crear la mesa de doblado inicial puede llevar algún tiempo, pero una vez formada, algunas partes se pueden reutilizar en el futuro.
Se puede introducir la misma o diferente información para cada pliegue de la pieza.
1) Estándares para flexión común.
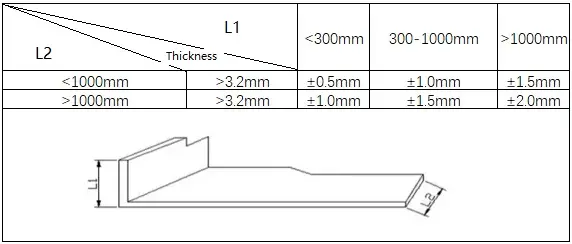
2) Patrones para flexión en Z
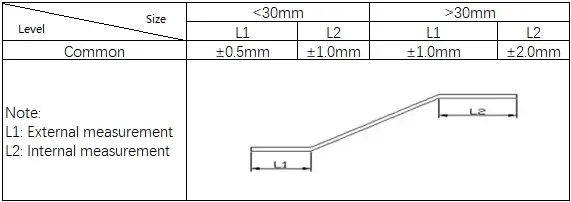
3) Patrones para doblar en V
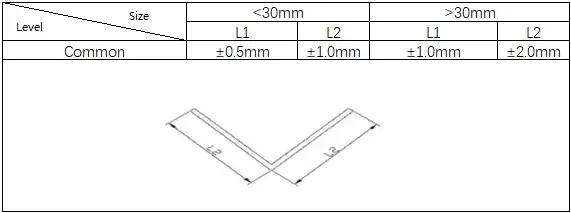
4) Patrones para doblar en U
Lectura relacionada: Calculadora de resistencia a la flexión en forma de V y U
3 . Método de deducción de flexión
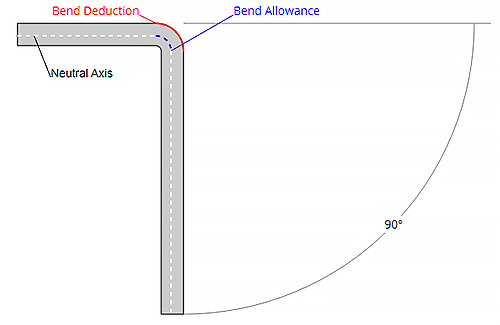
La deducción de curvatura es un término utilizado para describir la cantidad de sangría en el proceso de curvatura de chapa. Este es otro algoritmo simple para describir el proceso.
Las figuras 1 y 2 también se aplican a este concepto. Según el método de deducción de flexión, la longitud plana (LT) de la pieza es igual a la suma de las longitudes de las dos secciones planas que se extienden hasta el "punto de punta" (la intersección hipotética de las dos secciones planas), menos la flexión. deducción (BD).
Así, la longitud total de la pieza se puede expresar como se muestra en la ecuación (2):
LT = L1 + L2 – BD (2)
El valor BD se puede determinar u obtener de diversas fuentes, como proveedores de materiales de chapa, datos experimentales, experiencia, manuales de ingeniería con ecuaciones o tablas, etc.
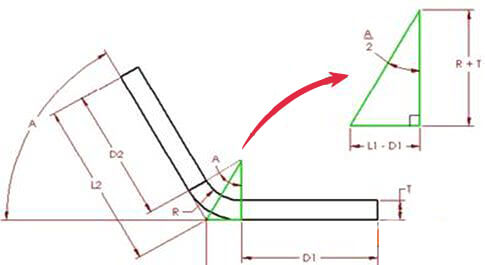
figura 3
4 . Relación entre el subsidio por flexión y la deducción por flexión
Es importante que los usuarios familiarizados con el método de deducción de pliegue comprendan la relación con el método de tolerancia de pliegue, que se adopta comúnmente en SolidWorks.
La relación entre ambos valores se puede deducir fácilmente utilizando las dos geometrías de flexión y despliegue de las piezas.
Comparando las ecuaciones (1) y (2), tenemos:
LT = D1 + D2 + BA (1) LT = L1 + L2 – BD (2)
Y por lo tanto,
D1 + D2 + BA = L1 + L2 – BD (3)
En la Figura 3, el ángulo A representa el ángulo de flexión, que describe el ángulo recorrido por la pieza durante la flexión, y también el ángulo del arco formado por el área de flexión, que se muestra en dos mitades.
Usando las dimensiones y principios de los triángulos rectángulos, podemos derivar las siguientes ecuaciones:
D1 = L1 – (R + T)TAN(A/2) (4) D2 = L2 – (R + T)TAN(A/2) (5)
Sustituyendo las ecuaciones (4) y (5) en la ecuación (3), podemos obtener la relación entre BA y BD:
BA = 2(R + T)TAN(A/2) – BD (6)
Y cuando el ángulo de curvatura es de 90 grados, esta ecuación se simplifica a:
BA = 2(R + T) –BD (7)
Estas ecuaciones (6) y (7) proporcionan un método conveniente para convertir de un algoritmo a otro, utilizando únicamente el espesor del material, el ángulo/radio de curvatura, etc.
Para los usuarios de SolidWorks, estas ecuaciones proporcionan un método sencillo para convertir el margen de pliegue en margen de pliegue.
El valor de tolerancia de plegado se puede utilizar para toda la pieza o para cada plegado individual, o se puede incluir en una tabla de datos de plegado.
5. Método del factor K
El factor K es un valor independiente que explica la flexión y el despliegue de chapa en diversos escenarios geométricos.
También es un valor independiente que se utiliza para calcular la tolerancia de flexión (BA) en diversas condiciones, como diferentes espesores de material, ángulos de flexión y radios.
Las figuras 4 y 5 se proporcionan para ayudar a aclarar la definición detallada del factor K.
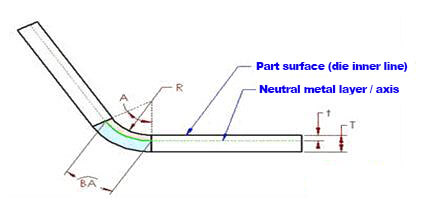
Figura 4
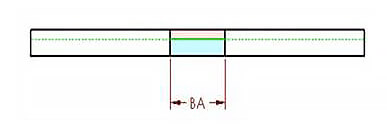
Figura 5
Podemos comprobar que existe un eje neutro en el espesor de la pieza de chapa. La chapa en este eje neutro en la zona de flexión no se estira ni se comprime, es decir, es la única zona que no se deforma durante la flexión.
Las figuras 4 y 5 muestran el límite entre las regiones rosa y azul.
Durante la flexión, la región rosa se comprime y la región azul se estira. Si la capa neutra de chapa metálica permanece sin deformar, la longitud de su arco en la región de plegado sigue siendo la misma ya sea que la pieza esté doblada o aplanada.
Como resultado, la tolerancia de flexión (BA) debe ser igual a la longitud del arco de la capa neutra en la región de flexión de la pieza de chapa, que se muestra en verde en la Figura 4.
La posición de la capa neutra de chapa depende de las propiedades de un material específico, como la ductilidad.
Se supone que la distancia entre la capa neutra de la chapa y la superficie es "t", o la profundidad desde la superficie de la pieza de chapa hasta el material en la dirección del espesor.
Como resultado, el radio del arco de la capa neutra se puede expresar como (R + t). Usando esta expresión y el ángulo de flexión, se puede calcular la longitud del arco de la capa neutra (BA).
BA = Pi(R+T)A/180
Para simplificar la definición de capa neutra de chapa y hacerla aplicable a todos los materiales, se introdujo el concepto de factor K.
La definición de factor K es: es la relación entre el espesor de la capa neutra de la chapa y el espesor total del material de la pieza de chapa. En otras palabras, el factor K se define como:
K = t/T
Por tanto, el valor de K siempre estará dentro del rango de 0 a 1. Si un factor K es 0,25, indica que la capa neutra se sitúa al 25% del espesor total del material de chapa.
Asimismo, si es 0,5 significa que la capa neutra se sitúa al 50% de todo el espesor y así sucesivamente.
Combinando las ecuaciones mencionadas anteriormente se puede obtener la siguiente ecuación (8):
BA = Pi(R+K*T)A/180 (8)
Por tanto, el valor de K siempre estará entre 0 y 1.
Si el factor K es 0,25, significa que la capa neutra se encuentra al 25% del espesor del material de chapa de la pieza.
Asimismo, si es 0,5 significa que la capa neutra se sitúa al 50% de todo el espesor y así sucesivamente.
El origen del factor K se remonta a fuentes tradicionales como proveedores de materiales de chapa, datos de pruebas, experiencia, manuales, etc.
Sin embargo, en algunos casos, es posible que el valor dado no se exprese como un factor K claro, pero aún así es posible encontrar la relación entre ellos.
Por ejemplo, si un manual o literatura describe el eje neutro como "colocado a 0,445 veces el espesor del material de la superficie de la chapa", esto podría interpretarse como un factor K de 0,445, lo que significa k = 0,445.
Cuando este valor de K se sustituye en la ecuación (8), se puede obtener la siguiente fórmula.
BA = A (0,01745R + 0,00778T)
Si la ecuación (8) se modifica mediante otro método, se calcula la constante de la ecuación (8) y se conservan todas las variables, se puede obtener lo siguiente:
BA = A (0,01745 R + 0,01745 K*T)
Al comparar las dos ecuaciones, es fácil determinar que 0,01745 * k = 0,00778 y, por lo tanto, k se puede calcular como 0,445.
Se descubrió que el sistema SolidWorks también proporciona un algoritmo de tolerancia de flexión para materiales específicos cuando el ángulo de flexión es de 90 grados. La fórmula de cálculo para cada material es la siguiente:
- Latón blando o cobre blando: BA = (0,55 * T) + (1,57 * R)
- Cobre semiduro o materiales como latón, acero al carbono y aluminio: BA = (0,64*T) + (1,57*R)
- Bronce, cobre duro, acero laminado en frío y acero para resortes: BA = (0,71 * T) + (1,57 * R)
De hecho, simplificando la ecuación (7) y estableciendo el ángulo de flexión en 90 grados, se puede calcular la constante y transformar la ecuación de la siguiente manera:
BA = (1,57 * K * T) + (1,57 *R)
Por lo tanto, comparando la fórmula de cálculo anterior, el valor de K para materiales de latón blando o cobre blando se puede obtener como 1,57xk = 0,55 o K = 0,35.
Utilizando el mismo método, es fácil calcular los valores del factor K para los diferentes tipos de materiales enumerados anteriormente.
- Material de latón blando o cobre blando: K = 0,35
- Cobre semiduro o materiales como latón, acero dulce y aluminio: K = 0,41
- Bronce, cobre duro, acero laminado en frío y acero para resortes: K = 0,45
Como se analizó anteriormente, existen varias fuentes de las cuales se puede obtener el valor del factor K, como proveedores de materiales, datos de pruebas, experiencia y manuales.
Para establecer un modelo de chapa preciso utilizando el método del factor K, es fundamental encontrar la fuente de factor K adecuada que cumpla con sus requisitos de ingeniería. Esto asegurará que los resultados físicos sean tan precisos como se desee.
En algunas situaciones, puede que no sea posible obtener resultados precisos utilizando un solo valor de factor K, especialmente cuando es necesario adaptarse a una amplia gama de escenarios de flexión.
En estos casos, es aconsejable utilizar el valor del margen de flexión (BA) directamente para un único pliegue de toda la pieza, o utilizar una tabla de pliegue para describir los diferentes valores de BA, margen de flexión (BD) o factor K. correspondientes a diferentes valores de A, R y T en todo el rango.
Además, se pueden utilizar ecuaciones para generar datos como el ejemplo de la tabla de plegado proporcionada por SolidWorks. Si es necesario, las celdas de la tabla de plegado también se pueden modificar en función de datos experimentales o empíricos.
El directorio de instalación de SolidWorks incluye tablas de tolerancia de plegado, tablas de deducción de plegado y tablas de factor K, que se pueden editar y personalizar según sea necesario.
- Calculadora de doblado de chapa metálica
6 . Resumen
Esta publicación proporciona una descripción general completa de los métodos de cálculo comunes y sus principios subyacentes utilizados en el diseño y fabricación de piezas de chapa metálica.
Cubre el cálculo de los márgenes de flexión, las deducciones por flexión y los factores K, y explica las diferencias entre estos métodos y sus interrelaciones.
Sirve como referencia útil para ingenieros y profesionales técnicos de la industria.
Observación:
- Tan se refiere a la representación simplificada de la función trigonométrica tangente.
- PI representa la constante pi (3.14159265…).

























































